Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 9. -
Вып. 1. - 2010. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-25-html/TITL-25.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-25-html/cont.htm
УДК 517.927
Метод
отображений для исследования обобщенной многоточечной задачи
функционально-дифференциальных уравнений
© 2010 г. Исраилов С. В.
В работе исследуется обобщенная многоточечная
функциональная краевая задача для функционально-дифференциальных уравнений
высших порядков (в том числе бесконечного порядка) из которой, как частные
случаи получаются многие краевые задачи (задача Валле Пуссена и другие многоточечные
краевые задачи). Для сведения данной задачи к некоторой системе нагруженных
интегральных уравнений применяется метод линейных отображений, и приводятся
достаточные условия существования решения.
Ключевые слова: многоточечная и функциональная краевая задача, метод
отображений, система нагруженных интегральных уравнений, операторное уравнение,
задача Николетти.
1.
Изучается
функционально-дифференциальное уравнение п-го
порядка
![]() (1)
(1)
с
краевыми условиями
![]() , (2)
, (2)
где
![]() ,некоторые функции своих аргументов в области
,некоторые функции своих аргументов в области ![]() причем значения функций
причем значения функций ![]() не выходят из сегмента
не выходят из сегмента ![]() , когда
, когда ![]() ;
; ![]() - функционалы, определенные в области
- функционалы, определенные в области ![]() ,
, ![]() - данные числа.
- данные числа.
Когда ![]() , и
, и ![]() не зависят от фазовых
коор-динат, задача (1), (2) и многочисленные ее разновидности изучались во
многих работах под названием задачи Валле–Пуссена или многоточечной краевой
задачи
не зависят от фазовых
коор-динат, задача (1), (2) и многочисленные ее разновидности изучались во
многих работах под названием задачи Валле–Пуссена или многоточечной краевой
задачи ![]() . В монографии
. В монографии ![]() некоторые виды задачи (1),(2) изучены для регулярных и
сингулярных дифференциальных уравнений. В такой общей постановке, по-видимому,
она не изучалась. Здесь нами применен нетрадиционный метод отображений с
последующим использованием идей исследования краевых задач для систем
обыкновенных дифференциальных уравнений из
некоторые виды задачи (1),(2) изучены для регулярных и
сингулярных дифференциальных уравнений. В такой общей постановке, по-видимому,
она не изучалась. Здесь нами применен нетрадиционный метод отображений с
последующим использованием идей исследования краевых задач для систем
обыкновенных дифференциальных уравнений из ![]() . Сама постановка задачи (1),(2) и реализация основной части
ее решения осуществлено в холодных подвалах погибающего Грозного под
артобстрелами и бомбежками зимой 1999-2000 годов. Под впечатлениями от ужасной
катастрофы, созданной в Чечне военными операциями, разрушившими всю
инфраструктуру жизнедеятельности людей, весной я бродил по развалинам домов и
улиц и мысленно задавал вопрос: кто и когда все это восстановит и будет ли это
при нашей жизни? Стертые с лица земли жилища, заводы, фабрики, школы, вузы,
библиотеки, театры и другие гражданские объекты, состояние душ людей, подавленных
невосполнимыми потерями, в сознании математика представлялись многоточечными
закрученными краевыми и функциональными условиями данного момента, а исторически
известная динамика способности к выживанию и возрождению самой Чечни и ее удивительного
народа, подвергающихся через каждые 40-50 к подобным катаклизмам, возмущенным
дифференциальным уравнением, описывающим состояние их бессмертия, исследование
которого надо проводить с учетом этих условий.
. Сама постановка задачи (1),(2) и реализация основной части
ее решения осуществлено в холодных подвалах погибающего Грозного под
артобстрелами и бомбежками зимой 1999-2000 годов. Под впечатлениями от ужасной
катастрофы, созданной в Чечне военными операциями, разрушившими всю
инфраструктуру жизнедеятельности людей, весной я бродил по развалинам домов и
улиц и мысленно задавал вопрос: кто и когда все это восстановит и будет ли это
при нашей жизни? Стертые с лица земли жилища, заводы, фабрики, школы, вузы,
библиотеки, театры и другие гражданские объекты, состояние душ людей, подавленных
невосполнимыми потерями, в сознании математика представлялись многоточечными
закрученными краевыми и функциональными условиями данного момента, а исторически
известная динамика способности к выживанию и возрождению самой Чечни и ее удивительного
народа, подвергающихся через каждые 40-50 к подобным катаклизмам, возмущенным
дифференциальным уравнением, описывающим состояние их бессмертия, исследование
которого надо проводить с учетом этих условий.
К вящему, но приятному удивлению
многих, решение такой сложной задачи восстановления разоренной жизни оказалось
под силу молодому президенту Чечни Р. Кадырову за несколько лет, которому и
посвящается данная работа, написанная под наплывом вышеприведенных раздумий,
где рассматривается дифференциальное уравнение бесконечного порядка.
![]()
![]() (3)
(3)
с
краевыми условиями
![]() (4)
(4)
где
![]() - фиксированное конечное натуральное число,
- фиксированное конечное натуральное число, ![]()
![]() , причем
, причем ![]() ;
;
![]()
![]() (5)
(5)
Если
![]() то условия (5) выпадают и задача (3)-(5) превращается в
задачу (1),(2); при
то условия (5) выпадают и задача (3)-(5) превращается в
задачу (1),(2); при ![]() уравнение (3)
становится дифференциальным уравнением бесконечного порядка
уравнение (3)
становится дифференциальным уравнением бесконечного порядка ![]() , которому при
, которому при ![]() или функция, не зависящие от
или функция, не зависящие от ![]() , посвящено некоторое количество работ, в том числе и по
изучению задачи Коши
, посвящено некоторое количество работ, в том числе и по
изучению задачи Коши ![]() . Отдельные многоточечные и функциональные кривые задачи для
бесконечных систем, в том числе и высшего порядка изучены в монографии
. Отдельные многоточечные и функциональные кривые задачи для
бесконечных систем, в том числе и высшего порядка изучены в монографии ![]() .
.
Задача (3)-(5) в такой постановке не
рассматривалась. Введем предварительно некоторые ограничения: функции ![]() и функционалы
и функционалы![]() , как непрерывные в смысле работ
, как непрерывные в смысле работ ![]() , считаются ограниченными:
, считаются ограниченными:
![]() (6)
(6)
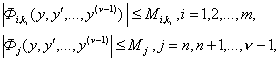 (7)
(7)
![]() некоторые числа. В области
некоторые числа. В области ![]() они удовлетворяют условиям Липшица:
они удовлетворяют условиям Липшица:
![]() (8)
(8)
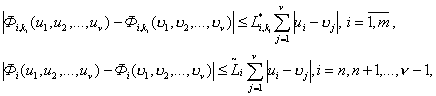 (9)
(9)
![]() - непрерывные функции,
- непрерывные функции, ![]() - числа, для любых векторов
- числа, для любых векторов
![]() из области
из области ![]() .
.
Возьмем в общем случаи пространство бесконечномерных
непрерывно-дифференцируемых вектор-функций ![]() и вектор-функцию
и вектор-функцию ![]() из него (при
из него (при ![]() имеем конечномерное пространство
имеем конечномерное пространство ![]() ) и линейные отображения.
) и линейные отображения.
![]() , (10)
, (10)
где,
![]() данная бесконечная
невырожденная матрица
данная бесконечная
невырожденная матрица ![]() бесконечного порядка
из множества
бесконечного порядка
из множества ![]() . Будем считать, что функции
. Будем считать, что функции ![]() таковы, что все функциональные
ряды в правых частях (10) и ряды, полученные их дифференцированием, равномерно
сходятся на сегменте
таковы, что все функциональные
ряды в правых частях (10) и ряды, полученные их дифференцированием, равномерно
сходятся на сегменте ![]() и по смыслу этих
равенств (10) последовательным дифференцированием при
и по смыслу этих
равенств (10) последовательным дифференцированием при ![]() и прирав-ниванием результата дифференцирования с правой
частью последующего равен-ства, получим систему дифференциальных уравнений:
и прирав-ниванием результата дифференцирования с правой
частью последующего равен-ства, получим систему дифференциальных уравнений:
![]() (11)
(11)
Для получения (11) мы
использовали равенства
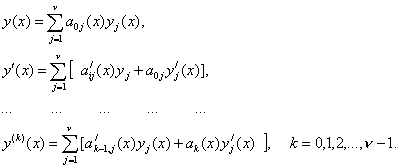
Эти
равенства (12) подставим в уравнение (3) и сгруппируем соответствующие
слагаемые (считается, что возможность всех этих операций обеспечивает функ-ции ![]() ) получим еще одно уравнение
) получим еще одно уравнение
![]() (13)
(13)
где
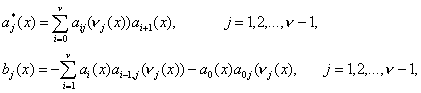 (14)
(14)
![]() - правая часть уравнения (3), в которую в место функций
- правая часть уравнения (3), в которую в место функций ![]() , подставлены выражения из (10). Теперь (11) и (3) объединим в
виде бесконечной системы.
, подставлены выражения из (10). Теперь (11) и (3) объединим в
виде бесконечной системы.
![]() (15)
(15)
где
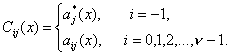 (16)
(16)
Матрицы
![]() и
и ![]() отличаются только
первой строкой, где
отличаются только
первой строкой, где
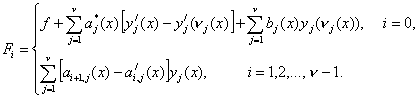 (17)
(17)
Пусть ![]()
![]() (18)
(18)
Тогда
![]() бесконечная система
(15) имеет единичное решение
бесконечная система
(15) имеет единичное решение
![]() (19)
(19)
2. Условие
(4) в расписанном виде означают равенства
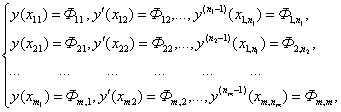 (20)
(20)
или кратко:
![]() (21)
(21)
На основании (10) из (21) имеем
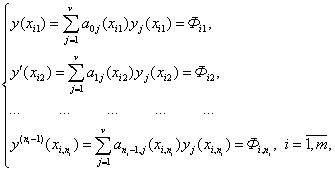 (22)
(22)
Естественно,
считается, что зависимость функционалов ![]() от фазовых коорди-нат
от фазовых коорди-нат
![]() учитывается с помощью
формул (10). Из равенства (20) находим
учитывается с помощью
формул (10). Из равенства (20) находим
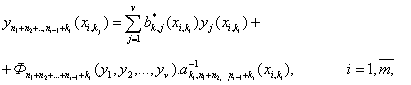 (23)
(23)
где
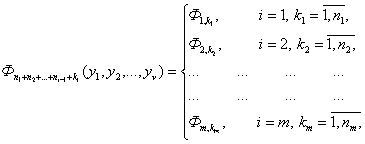
![]()
![]() (24)
(24)
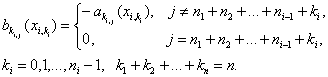
Обратимся
теперь к граничным условиям(5) для ![]() Отображения
(10)переводят их в равенства
Отображения
(10)переводят их в равенства
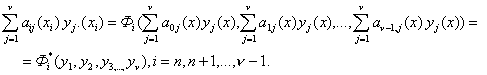 (25)
(25)
Из
них находим
![]() (26)
(26)
![]()
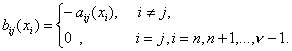 (27)
(27)
Обозначим
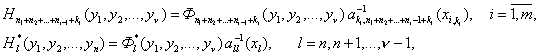 (28)
(28)
и объединим выражения (23) и (26):
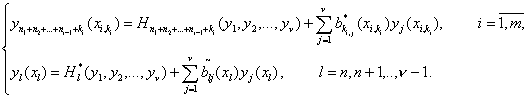 (30)
(30)
Система дифференциальных уравнений (18) с краевыми
условиями (30) экви-валента системе интегральных уравнений:
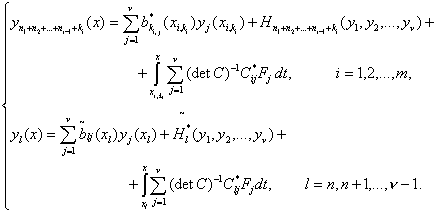 (31)
(31)
Положим
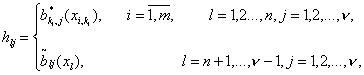 (32)
(32)
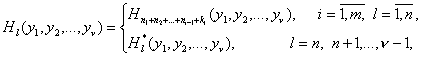 (33)
(33)
![]() (34)
(34)
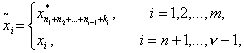 (35)
(35)
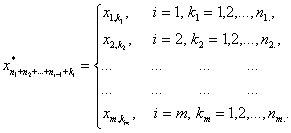 (36)
(36)
Тогда система нагруженных интегральных уравнений (31)
принимает вид
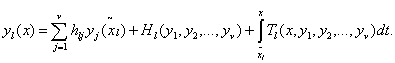 (37)
(37)
В силу уравнения (3) и отображений (10), как видно из
(17), функции![]() из (37), как функции фазовых координат, зависят от всех
функций
из (37), как функции фазовых координат, зависят от всех
функций ![]() и даже от
и даже от ![]()
![]() и
и ![]() , что необходимо учесть при исследовании интегральных
операторов (37).
, что необходимо учесть при исследовании интегральных
операторов (37).
Все что мы делаем по отображению задачи (3)-(5) в
задачу (19), (30) и построению ключевой системы (37) имеет смысл только в том
случае, если любая непрерывно-дифференцируемая вектор-функция ![]() , удовлетворяющая неравенствам
, удовлетворяющая неравенствам ![]() , где
, где ![]() -некоторые числа, отображает
-некоторые числа, отображает ![]() раз дифференцируемую функцию
раз дифференцируемую функцию ![]() с ее производными
с ее производными ![]() из пространства
из пространства ![]() -раз дифференцируемых функций в его некоторое подпространство
-раз дифференцируемых функций в его некоторое подпространство
![]() так, чтобы числовые значения
так, чтобы числовые значения ![]() и производных
и производных ![]() не выходили из
области
не выходили из
области ![]() .Поэтому между числами
.Поэтому между числами ![]() и
и ![]() , должны быть связи в
виде неравенств, обеспечивающих сказанное. Они получаются из (10) путем оценки
правых частей:
, должны быть связи в
виде неравенств, обеспечивающих сказанное. Они получаются из (10) путем оценки
правых частей:
![]()
![]() (38)
(38)
К
тому же числа ![]() , должны быть такими: любую вектор-функцию
, должны быть такими: любую вектор-функцию ![]() , удовлетворяющую неравенствам
, удовлетворяющую неравенствам ![]() , операторы в правых частях системы (37) должны отображать в
то же множество
, операторы в правых частях системы (37) должны отображать в
то же множество ![]() . Для этого, как в работе
. Для этого, как в работе ![]() это делалось неоднократно, на функции
это делалось неоднократно, на функции ![]() , функционалы
, функционалы ![]() и матрицу
и матрицу ![]() накладываются
ограничения, гарантирующие все действия,
которые мы совершали выше и будем совершать:
почленное дифференцирование, интегрирование, равномерная сходимость
функциональных рядов в том числе и двойных, сходимость числовых рядов и т.д.
накладываются
ограничения, гарантирующие все действия,
которые мы совершали выше и будем совершать:
почленное дифференцирование, интегрирование, равномерная сходимость
функциональных рядов в том числе и двойных, сходимость числовых рядов и т.д.
Как известно ![]() , бесконечные системы могут иметь как ограниченные так и
неограниченные решения. Здесь исследуются решения
, бесконечные системы могут иметь как ограниченные так и
неограниченные решения. Здесь исследуются решения ![]() , для которых
, для которых ![]() или
или ![]() при
при ![]() .
.
В этом случае, как будет показано, задача (19),(30) будет иметь единственное решение. Считается,
что числовой ряд ![]() сходится. Тогда из (38) следует, что и числовой ряд
сходится. Тогда из (38) следует, что и числовой ряд ![]() сходится. Нетрудно доказать, что векторфункции из множества
сходится. Нетрудно доказать, что векторфункции из множества ![]() равномерно ограничены
и равностепенно непрерывны. Действительно, возьмем
равномерно ограничены
и равностепенно непрерывны. Действительно, возьмем ![]() . Так как для любых двух значений
. Так как для любых двух значений ![]() справедливы равенства
справедливы равенства ![]() и так как из (10) и (38) следует
и так как из (10) и (38) следует ![]() , то
, то ![]() , следовательно, можно осуществить неравенство
, следовательно, можно осуществить неравенство ![]() -достаточно малое число.
Так же доказывается, что множество функций из
-достаточно малое число.
Так же доказывается, что множество функций из ![]() равномерно ограничено, замкнуто и выпукло: из (38) следует,
что
равномерно ограничено, замкнуто и выпукло: из (38) следует,
что ![]() , где
, где ![]() , поэтому
, поэтому ![]() .
.
Теперь остается доказать, что операторы
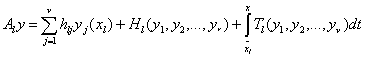 (39)
(39)
обладают
всеми свойствами элементов множества ![]() .
.
Прежде всего отметим, что в (39) присутствует
бесконечный![]() и алгебраические дополнения
и алгебраические дополнения ![]() . Естественно, полагается, что элементы бесконечной матрицы
. Естественно, полагается, что элементы бесконечной матрицы ![]() обеспечивают
выполнение соответствующих к ним требований из теории бесконечных определителей
обеспечивают
выполнение соответствующих к ним требований из теории бесконечных определителей
![]() и получение системы
(19) из (15) разрешением последней как алгебраической системы относительно
и получение системы
(19) из (15) разрешением последней как алгебраической системы относительно ![]() вполне закономерным, как и появление системы интегральных уравнений
вполне закономерным, как и появление системы интегральных уравнений ![]() или (37).
или (37).
Оценим оператор (39) по модулю с помощью выражений (6), (7),
(17), (32), (33), (34), (28), (29):
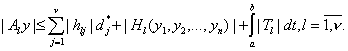 (40)
(40)
Из (28) и (33) для ![]() , имеем
, имеем
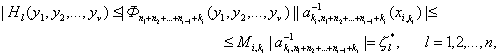 (41)
(41)
и при ![]()
![]() , (42)
, (42)
т.е.
![]()
![]() (43)
(43)
где
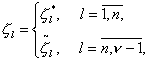 (44)
(44)
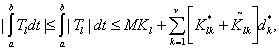 (45)
(45)
где
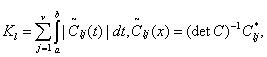
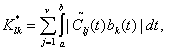
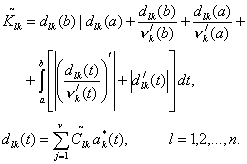 (46)
(46)
Пусть ![]() . Тогда из (17), (34) имеем:
. Тогда из (17), (34) имеем:
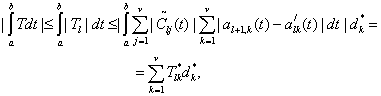 (47)
(47)
где
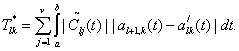 (48)
(48)
Теперь объединяя (45) и (47) имеем
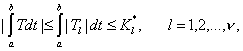
![]()
![]() (49)
(49)
где
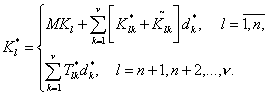 (50)
(50)
Из
(39), (43) и (49) получим
![]() , (51)
, (51)
где
![]() (52)
(52)
При
выполнении неравенств
![]() , (53)
, (53)
и
когда числовой ряд ![]() сходится, то и функциональные ряды
сходится, то и функциональные ряды ![]() также сходятся
равномерно для вектор-функции
также сходятся
равномерно для вектор-функции ![]() из множества
из множества ![]() и в силу неравенств (51), (53) операторы
и в силу неравенств (51), (53) операторы ![]() отображают множества
отображают множества ![]() в себя и ограничены.
в себя и ограничены.
Функции ![]() , как видно из (34) непрерывны, поэтому операторы (39) можно
дифференцировать по
, как видно из (34) непрерывны, поэтому операторы (39) можно
дифференцировать по ![]() :
:
![]() (54)
(54)
и
эти производные ограничены в силу свойств функции ![]() , т.к.
, т.к.
![]() , (55)
, (55)
причем
ряд ![]() будет сходится в силу
тех же свойств, поэтому выполняется и
неравенство
будет сходится в силу
тех же свойств, поэтому выполняется и
неравенство ![]() , что говорит о равномерной непрерывности, где
, что говорит о равномерной непрерывности, где ![]() любые точки из
любые точки из ![]() . Таким образом множества значений операторов является компактным
и в силу непрерывности операторов
. Таким образом множества значений операторов является компактным
и в силу непрерывности операторов ![]() по фазовым
координатам
по фазовым
координатам ![]() следует полная непрерывность
этих операторов и по принципу Шаудера имеет хотя бы одну неподвижную точку, что
равносильно существованию хотя бы одного решения интегральной системы (37),
следовательно, и задачи (19), (26).
следует полная непрерывность
этих операторов и по принципу Шаудера имеет хотя бы одну неподвижную точку, что
равносильно существованию хотя бы одного решения интегральной системы (37),
следовательно, и задачи (19), (26).
Все действия, которые совершались при
переводе задачи (3)-(5) в задачу (19),(26) можно реализовать и в обратном порядке
и от задачи (19), (26) мы переходим к
задаче (3)-(5), т.е. эти задачи эквивалентны.
Замечание 1. Если в уравнении (3) ![]() то в выражениях (17) для
то в выражениях (17) для ![]() будет отсутствовать сумма с производными функций
будет отсутствовать сумма с производными функций ![]() и оценки интегральных
операторов упрощаются.
и оценки интегральных
операторов упрощаются.
Замечание 2. О функционалах ![]() из краевой задачи (3)-(5) конкретно мало говорилось, ограничились
указанием на условия (7) и (9). Они могут быть линейными и нелинейными,
содержать выражения, зависящие от значений фазовых координат в
фиксированных точках
из краевой задачи (3)-(5) конкретно мало говорилось, ограничились
указанием на условия (7) и (9). Они могут быть линейными и нелинейными,
содержать выражения, зависящие от значений фазовых координат в
фиксированных точках ![]() , могут задаваться в интегральном виде и т.д. Например
, могут задаваться в интегральном виде и т.д. Например ![]() :
:
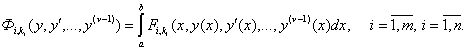 (56)
(56)
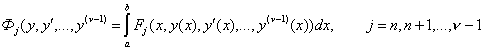 (57)
(57)
и
т.д.
Замечание
3. Если наложить дополнительные ограничения на элементы матрицы ![]() и если положить
и если положить ![]() , то из наших рассуждений получится точное решение задачи
(3), (20) в виде (37), когда и функционалы будут известными числами.
, то из наших рассуждений получится точное решение задачи
(3), (20) в виде (37), когда и функционалы будут известными числами.
Пусть задача (19), (26) имеет два
решения ![]() . Используя (3), составим разности и оценим их:
. Используя (3), составим разности и оценим их:
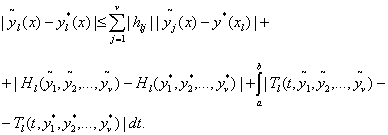 (56)
(56)
На
основании (8), (9), (28), (29), (17) и (34) имеем
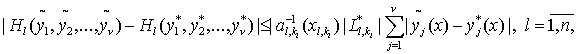 (59)
(59)
![]() (60)
(60)
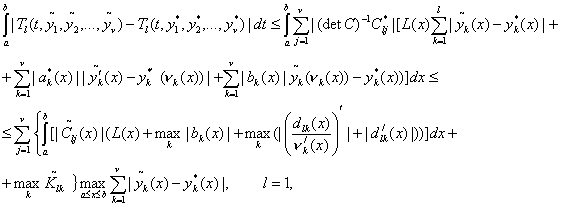
(61)
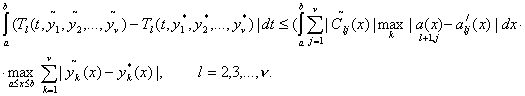 (62)
(62)
Поэтому
из (58) на основании (59), (60), (61),(62) получим:
![]() (63)
(63)
где
![]() , (64)
, (64)
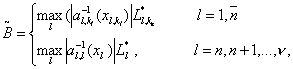 (65)
(65)
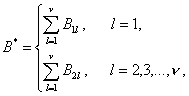 (66)
(66)
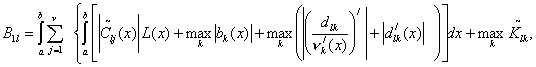 (67)
(67)
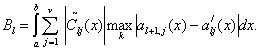 (68)
(68)
Если
предположить, что
B<1, (69)
неравенство
(63)приводит к противоречии, поэтому
![]()
Таким
образом, доказана
Т е о р е м а. Если функции ![]() и элементы матрицы
и элементы матрицы ![]() непрерывны и
непрерывно дифференцируемы, функция
непрерывны и
непрерывно дифференцируемы, функция ![]() и функционалы
и функционалы ![]() из (3), (4) непрерывны по совокупности аргументов и
удовлетворяют условиям (7)-(9), и так же выполняются условия (18),(38),(53) и
(63), то задача (3)-(5) имеет единственное
решение. Более тонкие теоремы существования и единственности получаются
методами из книг
из (3), (4) непрерывны по совокупности аргументов и
удовлетворяют условиям (7)-(9), и так же выполняются условия (18),(38),(53) и
(63), то задача (3)-(5) имеет единственное
решение. Более тонкие теоремы существования и единственности получаются
методами из книг![]() и функционального анализа
и функционального анализа ![]() . Главной целью данной работы является обоснование идеи
отображений для исследования задачи (3)-(5), успешно примененной и в других
работах
. Главной целью данной работы является обоснование идеи
отображений для исследования задачи (3)-(5), успешно примененной и в других
работах ![]() . Необходимо отметить, что в основном для исследования
многоточечных краевых задач применяется метод функции Грина. Известны
трудности, встречающиеся на пути нахождения фундаментальной системы решений для
линейных однородных дифференциальных уравнений с переменными коэффициентами,
наличие которой необходимо для построения функции Грина, соответствующей данной
конкретной задаче, поэтому ограничиваются соображениями ее существования. Много
стараний уходит на изучение ранее неизвестных свойств и оценок, необходимых для
разрешимости поставленной задачи и единственности решения
. Необходимо отметить, что в основном для исследования
многоточечных краевых задач применяется метод функции Грина. Известны
трудности, встречающиеся на пути нахождения фундаментальной системы решений для
линейных однородных дифференциальных уравнений с переменными коэффициентами,
наличие которой необходимо для построения функции Грина, соответствующей данной
конкретной задаче, поэтому ограничиваются соображениями ее существования. Много
стараний уходит на изучение ранее неизвестных свойств и оценок, необходимых для
разрешимости поставленной задачи и единственности решения ![]() В этом смысле кажется
ощутимым преимущество предложенного выше метода отображений с заранее
известными ограничениями на матрицу
В этом смысле кажется
ощутимым преимущество предложенного выше метода отображений с заранее
известными ограничениями на матрицу ![]() и другие параметры задачи.
и другие параметры задачи.
3.
Значительный научный интерес представляет обобщенный вариант задачи
(3)-(5) для бесконечной системы высших порядков в комбинированном виде:
![]() (70)
(70)
![]()
с
краевыми условиями
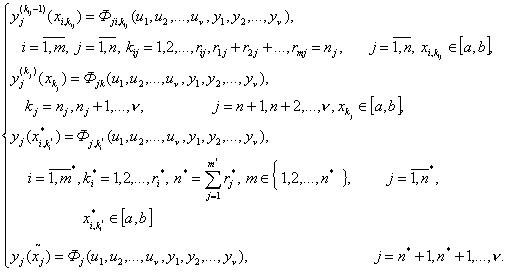 (71)
(71)
Когда ![]() -конечное число задача (70),(71) в пространстве
-конечное число задача (70),(71) в пространстве ![]() с помощью
вектор-функции
с помощью
вектор-функции ![]() и некоторой данной
матрицы
и некоторой данной
матрицы ![]() отображается в задачу
типа Николетти с нагруженными компонентами
отображается в задачу
типа Николетти с нагруженными компонентами ![]() . Если же
. Если же ![]() то берется квадратная
бесконечная матрица А (x) и отображение происходит с помощью вектор функций из
то берется квадратная
бесконечная матрица А (x) и отображение происходит с помощью вектор функций из
![]() применением теории
двухсторонних бесконечных определителей
применением теории
двухсторонних бесконечных определителей ![]()
Литература
1.
Кикурадзе И.Т. Некоторые
сингулярные краевые задачи для обыкновенных дифференциальных уравнений
Издательство Тбил. ун-та, Тбилиси 1975.
2.
Покорный Ю.В. Вопросы
качественной теории краевой задачи Вале-Пуссена. Дис. доктора физ-мат наук
Л.1980.
3.
Исраилов С.В., Юшаев
С.С.Многоточечные и функциональные краевые задачи для обыкновенных
дифференциальных уравнений. Издательский центр «Эль-фа». Нальчик.2004,с.445.
4.
Покорный Ю.В. О нулях
функции Грина задачи Вале-Пуссена. Математический сборник, том 199.№6,
105-135,Москва.2008.
5.
Левин А.Ю. О многоточечной
краевой задаче. Научный доклад высшей школы. Физ-мат. науки,1958, №5 с. 34-37.
6.
Исраилов С.В. Черкасов
И.Д. и др. Сингулярная задача Вале-Пуссено с нелинейными краевыми условиями,
Нефтепромысловое и нефтезаводская механика, Межвузовский сборник научных
трудов,1990, с.53-60, Грозный.
7.
Коробейник Ю.Ф.
Дифференциальные уравнения бесконечного порядка и бесконечные системы
дифференциальных. Изд. АН СССР. Сер. Матем., 1970, т. 34,№4. с. 881922.
8.
Коробейник Ю.Ф.
Операторы сдвига на числовых семействах, Изд-во Российского университета,
Ростов, 1983.
9.
Валеев К.Г., Жаутыков
О.Л. Бесконечные системы дифференциальных уравнений. Алма-Ата, Наука, 1974. с.
415.
10. Исраилов С.В. Полудифференцируемые функционалы в
вопросах исследования решений
операторных краевых задач для дифференциальных уравнений в банаховом
пространстве. Математический анализ и его применения, ЧГУ. Грозный.
11. Курпель Н.С., Шувар Б.А.Двусторонние операторные
неравенства и их применение. Киев. Науково думка. 1980.-268с.
12. Исраилов С.В., Юшаев С.С. Преобразование одних краевых
задач для ОДУ в другие. Функционально-дифференциальные уравнения и их приложения. Материалы третьей
Международной научной конференции, 24-27 сентября 2007г, с. 104-106, Махачкала.
13. Исраилов С.В., Юшаев С.С. Сведение одной многоточечной
краевой задачи для дифференциального уравнения n-го порядка к задаче Николлетти для системы. Современные
проблемы математики и смежные вопросы. Материалы международной конференции
«Мухтаровские чтения», 2008. с. 104-105, Махачкала.
Mapping method for research of the generalised multipointed problem of the functional-differential equations
Israilov
S. V.
In this work there is
investigated the generalised multipointed functional boundary value problem for
the functional-differential equations of the higher order (including an
infinite order) from which as special cases turn out many boundary value
problem (de la Vallee-Poussin’s solution and other multipoint boundary value
problem). The method of the linear mapping is applied to tabulate the given
problem to some loaded integral equation system, and sufficient condition of
the existence of a solution are resulted.
Keywords: multipointed and functional boundary value problem,
mapping method, loaded integral equation system, operator equation,
Nickoletti’s solution.
Домашний адрес:
364000 г.Грозный ,поселок Калинина,улица Дарвина № 67,
Исраилов Сейдахмед Вахидович
Исраилов Сейдахмед Вахидович, профессор кафедры «Алгебра и геометрия», Чеченского государственного университета
Darvin Street, 67
Kalinina Settlement
Grozny / 364 000 / Israilov Seidakhmed
Vakhidovich
Тел. Моб.: 8928 476 64 02, электронный адрес : segitov@mail.ru
Israilov Seidakhmed Vakhaevich, professor of "Algebra and Geometry Department"
of the Chechen State University.
Кафедра алгебры и геометрии
Чеченский государственный
университет
г. Грозный.
Поступила в редакцию 23.03.2010.