Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 9. -

Вып. 1. - 2010. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-25-html/TITL-25.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-25-html/cont.htm

 

УДК 621.396.96

 

УТОЧНЕНИЕ КОМПЛЕКСНОЙ ОГИБАЮЩЕЙ ДИСКРЕТНОГО СПЕКТРА В ЧАСТИ ЧАСТОТНОГО ДИАПАЗОНА

 

Ó 2010 г. Суханов В. В., Обысов А. В.

 

(sukhanov.doc)

 

Рассмотрена возможность детализации огибающей дискретного спектра на основе оценки локальных максимумов. Оценка получена с помощью дополнительной процедуры БПФ малой размерности. Приведено аналитическое описание способа детализации огибающей спектра в части частотного диапазона.

Ключевые слова: огибающая дискретного спектра.

 

В различных областях науки и техники часто приходится сталкиваться с вопросами фильтрации и спектрального оценивания параметров самых различных сигналов. Список задач, решение которых невозможно без применения аппарата фильтрации и спектрального оценивания сигналов постоянно расширяется, что вызывает неуклонный интерес исследователей к разработке новых и развитию известных методов, способов и алгоритмов обработки информации в частотной и пространственной области. По причине физических аналогий между временными и пространственными сигналами, а так же временной и пространственной обработкой, дальнейшее описание будет касаться только одной области – частотной. Обработка информации в частотной области популярна по причине возможности реализации вопросов накопления, обнаружения сигналов, измерения их параметров, преобразования и др. с меньшими вычислительными затратами и потерями, чем при обработке во временной области.

Таким образом, широкое распространение методов и способов спектрального оценивания подтверждает актуальность совершенствования известных из них и разработки новых. По этой причине целью настоящей статьи является разработка нового способа уточнения формы спектра сигнала, обладающего достаточной точностью и экономичного с точки зрения вычислительных затрат.

При обработке цифровой информации, для перехода от временного к спектральному представлению сигнала и обратно, применяются дискретное преобразование Фурье (ДПФ) и обратное ДПФ (ОДПФ) [2, 3, 4]. На практике как ДПФ, так и ОДПФ чаще всего реализуются при помощи алгоритмов прямого и обратного быстрых преобразований Фурье (БПФ), которые по конечному эффекту являются полными аналогами ДПФ и ОДПФ, но позволяют существенно уменьшить вычислительные затраты.

Цифровая обработка сигнала предполагает предварительную его дискретизацию при помощи аналого-цифрового преобразователя. После проведения такой операции s-й отсчёт дискретной выборки сигнала конечной длительности будет иметь вид

 

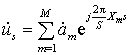,                                                     (1)

 

где M – число гармонических составляющих в спектре исходного сигнала;

 – комплексная амплитуда m-й составляющей спектра;

S – число дискретных отсчётов в выборке;

Хm =fmSΔT – частота m-й составляющей, выраженная в относительных единицах.

Операция ДПФ проводится в соответствии с выражением

, k=0÷S–1.                                          (2)

 

На рис. 1 показаны дискретный спектр сигнала , полученный в результате дискретизации сигнала и выполнения БПФ, и модуль его комплексной огибающей в виде пунктирной линии. Видно, что операция дискретизации привела к тому, что непрерывный исходный спектр определен только в отдельных точках. Расстояние между этими точками определяется длительностью исходного сигнала.

 

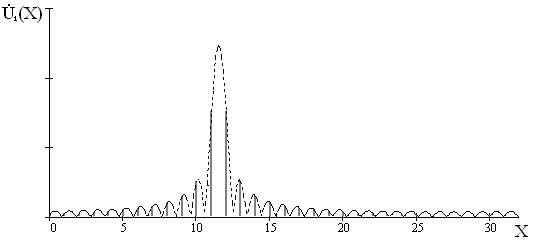
Рис. 1. Дискретный спектр сигнала и модуль его комплексной огибающей

 

На рис. 2 показаны соответственно дискретный спектр сигнала , отличающегося от сигнала  и модуль его комплексной огибающей в виде пунктирной линии.

 

Рис. 2. Дискретный спектр сигнала и модуль его комплексной огибающей

 

Из рисунков 1 и 2 видно, что, несмотря на то, что спектры исходных сигналов существенно отличаются (спектр исходного сигнала  имеет один максимум, а спектр сигнала  два), операция дискретизации привела к тому, что дискретные спектры обоих сигналов оказались близки по форме.

На практике, особенно с учётом шумов, всегда сопровождающих измерения и дополнительно искажающих спектры, подобное явление может стать источником грубых ошибок в оценке параметров спектров. Кроме того, при построении частотных и пространственных спектров низкое разрешение приводит к эффекту маскирования слабых сигналов более сильными [1]. Следовательно, необходимо определить промежуточные составляющие спектра.

На выходе сигнального фильтра обеспечивается наибольшее отношение сигнал-шум, поскольку сигнал регистрируется именно в этом фильтре. Напряжения в других фильтрах, где сигнал не регистрируется, а присутствует только шум, зачастую не представляет интереса. Поэтому, при спектральном анализе, наибольший интерес представляет получение максимальной информации в районе сигнальных фильтров. Доля энергии, которая приходится на «сигнальный» и соседние с ним частотные фильтры составляет более 96% всей энергии спектра сигнала, тогда как энергия шума распределена равномерно вдоль всей частотной оси.

В настоящее время, для детализации спектра, наибольшее распространение получил способ дополнением нулями исходной последовательности с последующим БПФ. Этот способ отличают простота и точность определения комплексной огибающей спектра в точках, соответствующих спектральным отсчётам. Однако, детализация комплексной огибающей спектра, известными способами [2, 3, 4], позволяет получать промежуточные спектральные составляющие во всей рабочей полосе частот. Задачи, требующие исследования всей доступной полосы частот возникают далеко не всегда. Они характерны для этапов поиска и обнаружения неизвестного сигнала. После того, как сигнал оказывается обнаруженным, необходимость анализа формы спектра во всём частотном диапазоне, как правило, отпадает. Так, для оценивания спектра, изображенного на рис. 1 и 2, достаточно проанализировать полосу частот от 8 до 15 (обозначим это окно – L). Для этого необходимо уточнить комплексную огибающую дискретного спектра в узкой полосе частот.

Способ детализации комплексной огибающей спектра эхосигнала в части частотного диапазона, состоит из следующих последовательных операций:

1. Выполнение операции БПФ над исходной последовательностью данных.

2. Выделение локального участка спектра, содержащего максимальный сигнальный фильтр и по L/2 сигнальных фильтров с каждой стороны. Число выделенных отсчётов должно составлять 2n.

3. Выполнение операции ОБПФ над L отсчётами.

4. Умножение каждого отсчёта полученной последовательности L на комплексные числа вида , где b – выраженная в относительных единицах частота, на которой необходимо получить промежуточный отсчёт в спектре, i – номер отсчёта исходного спектра, входящий в L.

5. Выполнение операции БПФ над L отсчётами.

Выделенную последовательность в пункте 2 будем называть «усечённым» спектром или «усечённой» последовательностью спектральных отсчётов.

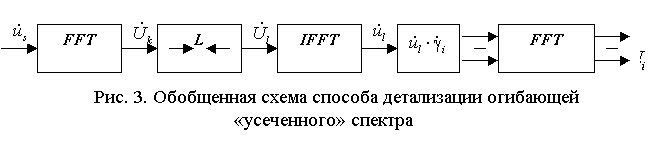
На рис. 3 показана обобщенная схема способа детализации огибающей части доплеровского спектра, заключающегося в последовательном выполнении БПФ на L отсчётов с доворотом по фазе «усечённой» последовательности r раз.

 

Аналитически способ, заключающийся в детализации части частотного диапазона можно выразить следующим образом.

Первое (полное – над всей исходной последовательностью) БПФ:

 

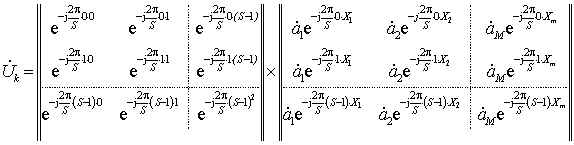    (3)

 

где первая матрица – это матрица преобразования Фурье, размером S×S;

вторая матрица – вектор-столбец отсчётов исходного сигнала, размером S×M.

После определения гармонической составляющей с максимальной амплитудой и соседних с ней (L-1) гармоник получим выборочный («усечённый») спектр. Это эквивалентно умножению матрицы ДПФ на диагональную матрицу (фильтры в районе максимума) размером L×S. Диагональная матрица предназначена для снятия зависимости от начальной фазы в спектре исходного сигнала.

После «отсечёния» гармоник не принадлежащих L получим матрицу «выборочного» ДПФ:

 

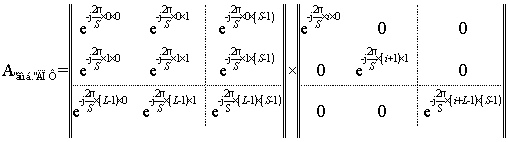    (4)

 

где i – первый отсчёт «усечённого» спектра;

L – число отсчётов «усечённого» спектра.

После ОДПФ «усечённого» спектра получим:

 

 

,

 

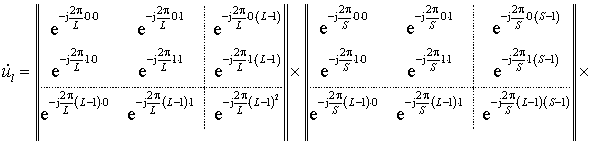
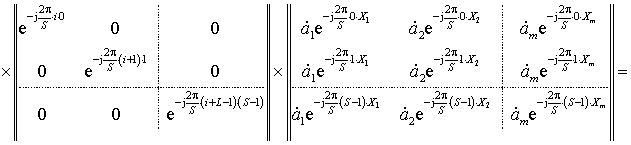
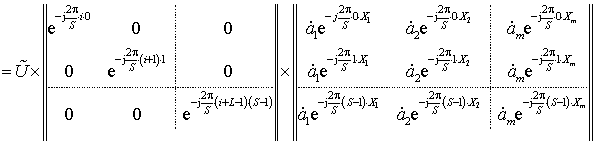Каждый элемент матрицы  имеет вид

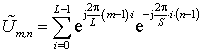,                                                      (5)

где m – номер строки 1…L, а n – номер столбца 1…S.

Выражение (5) представляет собой сумму членов геометрической прогрессии, знаменатель которой равен:

 

 

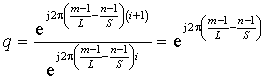
С учётом этого выражение (5) можно переписать

 

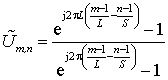                                                 (6)

 

Разделив выражение (6) на , и умножив на  [1], получим

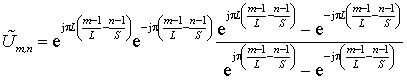                  (7)

 

Применив в дробной части выражения (7) формулы Эйлера [1] получим

 

 

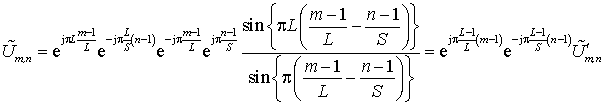
где 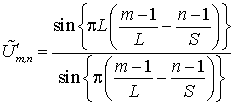 – весовая функция, описывающая комплексную огибающую «усечённого» спектра размером L, из исходного спектра размером S.

Таким образом, матрицу  можно переписать в виде:

 

 

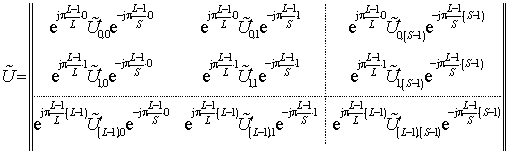
Таким образом, ОБПФ над частью отсчётов спектра БПФ эквивалентно тому, что исходная последовательность доворачивается по фазе (умножаются матрицы ДПФ и диагональная на L отсчётов) и суммируется с L вещественными весовыми функциями вида  и снова доворачивается по фазе.

Функция 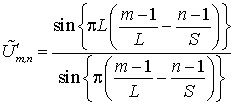 достигает максимума при  (правило Лопиталя).

Для первой строки: m = n = 1. Для второй строки:  и т. д.

Сигнал  представляет собой выборку во временной области числом L, огибающая которой совпадает с огибающей исходного сигнала, то есть его l-й отсчёт соответствует (пропорционален)  отсчёту исходного сигнала. Однако, каждый отсчёт «усечённого» сигнала, во временной форме, получен в результате перемножения и суммирования всех отсчётов исходного сигнала (операция ДПФ), и учитывает комплексную огибающую исходного спектра длиной S. Его энергия с точностью до нескольких процентов равна энергии исходного сигнала (в зависимости от длины «усечённой» выборки L). Таким образом, каждый отсчёт «усечённого» сигнала представляет произведение и сумму исходных отсчётов, довернутых по фазе на величину . Первый множитель данного произведения определяет доворот по фазе «усечённой» последовательности, а второй множитель определяет доворот по фазе всей исходной последовательности отсчётов.

Итоговое значение «усечённого» спектра, для описываемого способа детализации, примет вид:

 

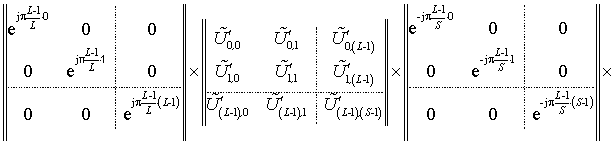
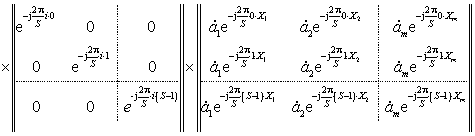       (8)

 

где первая матрица – матрица ОДПФ, размером L×L;

вторая матрица – весовая функция, описывающая комплексную огибающую «усечённого» спектра размером L, из исходного спектра, размером L×S;

третья матрица – определяет доворот по фазе между отсчётами «усечённой» последовательности, размером L×S;

четвертая матрица – определяет доворот по фазе между отсчётами исходной последовательности отсчётов, размером S×S;

пятая матрица – вектор-столбец отсчётов исходного сигнала, размером S×S.

Для получения промежуточных отсчётов «усечённого» БПФ необходимо каждый отсчёт  умножить на комплексные числа вида  и произвести операцию БПФ.

На рис. 4 и 5 показаны дискретные спектры исследуемых сигналов, уточнённые в узкой полосе частот, для сигналов, представленных на рис.1 и 2 соответственно. Из рисунков видно, что, как и на рис. 1 и 2 форма исходных спектров восстановлена достаточно точно.

 

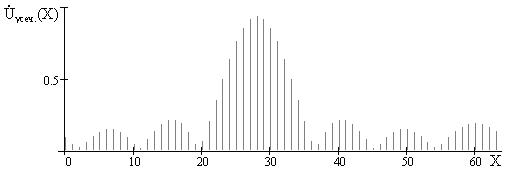
Рис. 4. Дискретный спектр сигнала , при последовательном

выполнении БПФ с доворотом по фазе в узкой полосе частот

 

Для построения каждого из этих спектров понадобилось 5452 операций комплексного умножения, что соизмеримо с числом вычислительных операций над исходной последовательностью без дополнения нулями . Экономия вычислительных затрат, по сравнению со способом, основанным на дополнении нулями, для получения подобной детализации, составляет 109236 операций комплексного умножения (в 21 раз меньше). Очевидно, что с увеличением числа исходных отсчётов и степени уточнения экономия вычислительных затрат будет ещё больше.

 

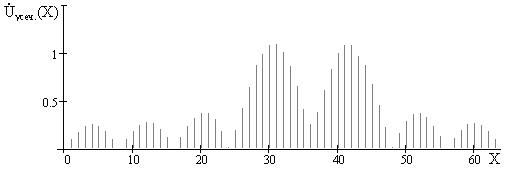
Рис. 5. Дискретный спектр сигнала, при последовательном

выполнении БПФ с доворотом по фазе в узкой полосе частот

 

Из рисунков видно, что форма исходных спектров, в части частотного диапазона, при обработке сигналов предложенным способом, воспроизводится без искажений, что свидетельствует о достижении поставленной цели.

Таким образом, можно сделать выводы, что:

1. Многие задачи науки и техники решаются при помощи методов и способов спектрального оценивания.

2. Среди многообразия различных способов особое место занимают способы, использующие аппарат дискретного (быстрого) преобразования Фурье.

3. Дискретизация спектра исходного непрерывного сигнала, неизбежно возникающая при выполнении операции ДПФ (БПФ) может привести к возникновению грубых ошибок при оценке параметров спектров, что требует применения способов уточнения формы спектра.

4. Недостатком существующих способов уточнения формы спектра является рост вычислительных затрат и детализация во всём рабочем диапазоне частот и углов, что ограничивает их применимость.

5. Предложенный способ детализации спектров дискретных сигналов путём последовательного выполнения БПФ с доворотом по фазе «усечённой» последовательности позволяет существенно (в десятки раз) уменьшить число вычислительных затрат, что свидетельствует о возможности его применения в системах обработки информации, работающих в реальном времени.

 

Литература

 

1. Варюхин В. А. Основы теории многоканального анализа. Киев: ВА ПВО СВ им. А. М. Василевского, 1993. 170 с.

2. Гоноровский И. С. Радиотехнические цепи и сигналы. Учебник для вузов. М. Радио и связь, 1986. 482с.

3. Марплмл. С. Л. Цифровой спектральный анализ и его приложения. М.: Мир, 1990. 291с.

4. Э. Айфичер; Б. Джервис. Цифровая обработка сигналов: практический подход, 2-е издание. – М.: Издательский дом «Вильямс», 2004. 1000с.

 

REDETERMINATION OF DESCRETE SPECTRUM COMPLEX ENVELOPE IN A PART OF FREQUENCY RANGE

 

Sukhanov V. V. , Obisov A. V.

 

The possibility of descrete spectrum envelope detailing on the basis of local maximums is considered. Estimation is obtained by additional procedures of FFT of small size. The analytical description of the manner of spectrum envelope detailing in a part of frequency range is given.

Key words: descrete spectrum envelope.

 

Военная академия войсковой ПВО ВС РФ имени Маршала Советского Союза А. М. Василевского.

Russian Federation Armed Forces Air Defense Academy named after Marshal of the Soviet Union A. M. Vasilevsky

Поступила в редакцию 23.03.2010.