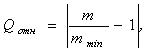Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 9. -

Вып. 2. - 2010. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/TITL-26.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/cont.htm

УДК 623.4.02

МЕТОДЫ КОЛИЧЕСТВЕННОЙ ОЦЕНКИ

ОРГАНИЗАЦИОННЫХ СТРУКТУР СИСТЕМ УПРАВЛЕНИЯ

СПЕЦИАЛЬНОГО НАЗНАЧЕНИЯ

Ó 2010 г. Ангелов А. Н., Кучерявый А. В.

(angelov.doc)

В статье изложены аналитические методы оценки организационных структур систем управления специального назначения.

Ключевые слова: система управления, математическая модель, элемент системы.

Изменение системы управления специального назначения в рамках перехода к новому облику требует выбора рациональной структуры системы управления, что весьма актуально в настоящий момент.

В организационной структуре любой системы управления присутствует иерархическая структура. Поэтому, при проектировании организационной структуры, выбор и оценка структуры системы управления является наиболее важной задачей.

Сложность проблемы проектирования организационной структуры конкретной системы управления, требует применения при ее решении методов и моделей системного анализа.

Одним из первых этапов является выбор формы структуры. При этом следует иметь в виду, что форма влияет на реализацию принципов целостности и свободы структурных подразделений.

Оптимизация формы структуры системы управления, которая обеспечивала бы сбалансированность между централизованным и децентрализованным управлением является основной проблемой повышения эффективности управления в сложных условиях интенсивного противоборства сторон. Для реализации этой задачи требуется механизм количественной оценки структур. В качестве такого механизма может быть применен метод информационной оценки степени целостности α и коэффициента использования компонентов системы управления β, которые могут интерпретироваться как оценки устойчивости организационной структуры при предоставлении свободы структурным подразделениям или как оценки степени централизации (децентрализации) управления.

Эти оценки получаются из соотношения, определяющего взаимосвязь системной , собственной и взаимной сложности системы

. (1)

Системная сложность представляет собой суммарную сложность (содержание) элементов системы вне связи их между собой (в случае прагматической информации – суммарную сложность элементов, влияющих на достижение цели). Собственная сложность представляет содержание системы как целого (например, сложность ее использования). Взаимная сложность характеризует степень взаимосвязи элементов в системе (т. е. сложность ее устройства, схемы, структуры).

Делением членов выражения (1) на получаются две важные сопряженные оценки:

; (2)

; (3)

причем , т. е. .

Первая из них (2) характеризует степень целостности, связности, взаимозависимости элементов системы; для организационных систем α может быть интерпретирована как характеристика устойчивости, управляемости, степени централизации управления. Вторая (3) – самостоятельность, автономность частей в целом, степень использования возможностей элементов. Для организационных систем β удобно называть коэффициентом использования элементов в системе.

Знак минус в выражении (2) введен для того, чтобы было положительным, поскольку в устойчивых системах, для которых характерно , формально имеет отрицательный знак. Связанное (остающееся как бы внутри системы) содержание характеризует работу системы на себя, а не на выполнение стоящей перед ней цели (чем и объясняется отрицательный знак (), что важно учитывать при формировании организационных структур систем управления.

Для пояснения принципов оценки структур приведем упрощенный пример сравнительного анализа структур (рис. 1), которые отображают варианты организационной структуры систем управления, включающие разное число подчиненных подразделений и их активных средств.

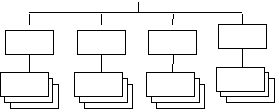
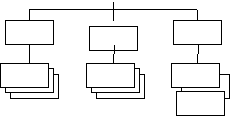
а б

Рис. 1. Структуры: а – четырехподчиненного состава;

б – трехподчиненного состава

Естественно, цель всех этих структур – управление деятельностью элементов самого нижнего уровня структуры, т. е. решение задач выбора, какому из подчиненных поставить задачу.

В методе принято, что каждый элемент имеет информативность J = 1 бит.

Сравнивая варианты, приведенные на рис. 1, получим результаты.

Расчет системной сложности структур С_с:

_{; .}

Расчет собственной сложности системы С_о:

; .

Расчет взаимной сложности С_в определяется как

; .

Тогда степень целостности системы, взаимозависимости, устойчивости, управляемости, степени централизации определяется:

; .

Степень самостоятельности, автономности:

; .

Количественные различия коэффициентов целостности и степени использования элементов в данном примере небольшие, поскольку обе структуры трехуровневые и незначительно отличаются друг от друга. Однако оценки являются основой для сравнительного анализа, и даже небольшие различия со временем могут существенно повлиять на результаты функционирования системы управления. Поэтому можно сделать вывод, что первая структура (рис. 1, а) обеспечивает большую централизацию управления, а вторая структура (рис. 1, б) предоставляет большую автономию огневым средствам.

Рассмотренный метод оценки позволяет получить наглядную количественную оценку структур систем управления. Основной его недостаток – отсутствие чувствительности к связанности системы, что требует применения дополнительных методов оценки.

Такой подход присутствует в теории графов, которая предлагает набор структурно-топологических характеристик, позволяющих провести оценку структуры системы или ее отдельных подсистем.

К числу таких характеристик относят связность , степень управляемости Y, неравномерность распределения связей , структурную компактность , диаметр d структуры.

Связность – наименьшее число вершин, удаление которых из графа приводит к несвязному (содержащему изолированные вершины) или тривиальному (состоящему из одной вершины) графу. Для оценки связности часто используют упрощенный показатель

,

где n – число вершин, m – число связей в структуре.

Данная характеристика позволяет выделить наличие обрывов, висячие вершины и т.д.

При этом R интерпретируется как мера избыточности структуры по связям. Для многих видов топологических структур значение R вполне конкретно. Так, для кольцевой структуры , для радиальной , а для древовидной она определяется видом дерева.

Степень управляемости различных вариантов структуры системы в ряде работ оценивается по отношению количества управляемых компонентов Xu, с учетом их важности q_xui к общему количеству I компонентов вектора, характеризующих состояние системы:

,

где I=m+n.

Этот показатель в определенной степени отражает управляемость, ибо в абсолютно управляемых системах расход ресурсов на достижение требуемого эффекта от системы будет минимальным.

Для оценки равномерности распределения связей в структуре системы, имеющей n вершин элементов и m связей, вводится понятие «средняя степень вершины»

=.

Его использование позволяет определить неравномерность распределения связей как

²=,

где p_i – действительная степень вершины, которая определяется количеством связей исходящих из вершины.

Следовательно, характеризует недоиспользование возможностей заданной структуры в достижении максимальной связности.

Для количественной оценки структурной компактности вводится параметр, отражающий близость элементов системы между собой. Близость двух элементов i и j – между собой определяется через минимальную длину пути для ориентированного графа. Тогда величина

, ij.

отражает общую структурную близость элементов между собой в системе.

Для количественной оценки структурной компактности очень часто используют относительный показатель

где m_min = n(n–1) – минимальное значение компактности для структуры полного графа. Структурную компактность можно характеризовать и другой характеристикой – диаметром структуры

.

Учитывая преобладающий информационный характер связей в системе, можно сделать вывод, что Q_отн и d оценивают инерционность информационных процессов в системе, а при равных значениях ² и R их возрастание отражает увеличение числа разделяющих связей в структуре, тем самым говоря о снижении общей надежности.

Удобство предварительной оценки структуры системы управления перечисленными характеристиками теории графов в том, что все они имеют ясный физический смысл, а главное, легко вычисляемы. Однако эти характеристики жестко коррелированны и для оценки структуры необходимо определить пределы их изменения.

На рис. 2 показаны законы распределения параметров типовой древовидной структуры системы управления.

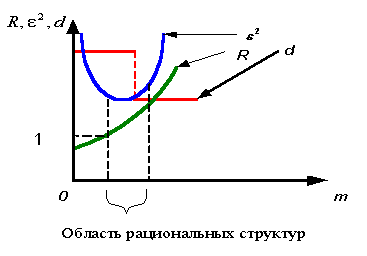
Рис. 2. Законы распределения параметров типовой древовидной структуры

Показатель связности R хорошо реагирует на любые изменения информационных связей системы. Фактически он показывает усредненное количество двух сторонних связей, приходящихся на один элемент. Принято считать, что при связность системы достаточна и без избыточности, при меньших значениях R система испытывает дефицит связей.

Проекция точки перегиба функции ² на ось оm указывает центр интервала переменной m, определяющего область рациональных структур. Окончательный выбор делается по величине диаметра d структуры, который показывает близость источника. Оптимальным вариантом будет тот, который при примерно равных значениях других показателей имеет минимальный диаметр. Для системы управления специального назначения это очевидно, так как удаленность источника определяется промежуточными инстанциями сбора и обработки информации. Чем длиннее цепочка пунктов обработки информации, тем сильнее снижается достоверность информации, ухудшаются точностные показатели, накапливается запаздывание.

Из рис. 2 видно, что область, в которой могут находиться рациональные структуры, довольно мала, что свидетельствует о приемлемой избирательности способа предварительной оценки структур на основе теории графов.

Оба метода количественной оценки структур представляют большой интерес при исследованиях систем управления специального назначения. Так метод информационной оценки целостности системы дает возможность выбора и оптимизации вида и формы структуры на этапе ее формирования. Структурно-топологические характеристики структуры позволяют исследовать влияние информационных связей на многие свойства системы (устойчивость, управляемость, производительность и т. д.). Автор видит перспективу их применения при анализе, оптимизации и управлении структурой системы управления.

ЛИТЕРАТУРА

1. Советов Б. Я., Цехановский В. В., Чертовский В. Д. Теоретические основы автоматизированного управления: Учебник. – М., 2006. 457 с.

2. Меньков А. В., Острейковский В. А. Теоретические основы автоматизированного управления: Учебник. – М., 2005. 639 с. 

3. Антонов А. В. Системный анализ: Учебник для вузов. – М., 2004. 454 с.

4. Спицнадель В. Н. Основы анализа: Учебное пособие. – СПб., 2000. 326 с.

5. Кристофедес Н. К. Теория графов. Алгоритмический подход. – М.: 1978. 427с.

Method of scoring special - purpose control systems

organizational structures

Angelov A. N., Kucheryavyi A. V.

The article deals with the methods of scoring special-purpose control systems organizational structures.

Key words: a control system, mathematical model, a system element.

Военная академия войсковой ПВО Вооруженных Сил Российской Федерации имени Маршала Советского Союза А.М. Василевского (ВА ВПВО ВС РФ)

Поступила в редакцию 28.05.2010.
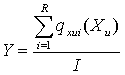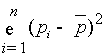