Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 9. -

Вып. 2. - 2010. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/TITL-26.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/cont.htm

УДК 511

Исследование свойств делимости полиномиальных коэффициентов и степеней методом формальных степенных рядов

Ó 2010 г. Мануилов Н. Ф.

(manuilov-2.doc)

В статье методом формальных степенных рядов доказано несколько новых результатов по теории делимости целых чисел и следствий из них, представляющих новые и известные свойства делимости полиномиальных коэффициентов и степеней.

Ключевые слова: степенной ряд, дифференциальный оператор, отношение делимости в кольце целых чисел, отношение сравнения, наибольший общий делитель, простое число.

В статье доказано следующее предложение

Теорема 1. Пусть наибольший общий делитель целых неотрицательных чисел m₁,m₂, …, m_s равен 1. Тогда при любых: целых числах a_1, a_{2 ,…,} a_s и натуральном n выполняется сравнение (1)

,

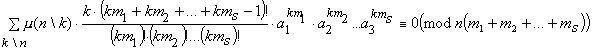где – функция Мёбиуса.

Из теоремы 1 получен ряд следствий, в частности известный факт:

Следствие 1. Если а – целое число и n - натуральное число, то

,

(см. 1, стр. 315).

В доказательстве теоремы 1 существенно используется теория формальных степенных рядов, в частности, установленный ниже следующий факт.

Лемма 2.7. Пусть ряд f, , имеет целые коэффициенты, ,

(D_j – оператор (8) – см. далее, j = 1,2,…,s) и m₁, m₂,…,m_s – какая-нибудь система взаимно простых целых неотрицательных чисел .

Тогда при любом натуральном числе n коэффициенты ряда

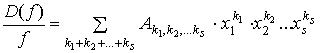
удовлетворяют сравнению

.

1. Об одном порядке на множестве N^s

Пусть N = {0, 1, 2…}. На множестве зададим бинарное отношение следующим образом:

(2)

тогда и только тогда, когда

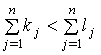
или найдется номер такой, что

.

Кроме того на 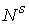будем рассматривать бинарную операцию +:

Лемма 1.1. Алгебраическая система есть вполне упорядоченный моноид.

Доказательство опускаем.

2. Некоторые сведения из теории формальных степенных рядов.

Пусть - кольцо формальных степенных рядов от переменных с коэффициентами из поля действительных чисел .

Любой формальный ряд f можно записать в виде

, (3)

где порядок слагаемых определяется порядком (2) на множестве индексов коэффициентов

.

На множестве 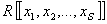зададим числовую функцию || ^. ||:

,

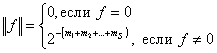где - индекс первого не равного нулю коэффициента ряда f в (3)

Так как

,

то числовая функция || ^. || есть неархимедово нормирование кольца

[3, стр. 546].

Множество 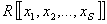превращается в полное метрическое пространство, если метрику 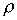задать формулой

, (4).

Кольцевые операции оказываются непрерывными в топологии, порождаемой метрикой (4), множество многочленов всюду плотно в и любой формальный ряд (3) является сходящимся в заданной топологии, то есть элемент (3) можно рассматривать, как предел последовательности частичных сумм. Легко доказываются следующие критерии сходимости рядов и произведений в пространстве .

(5). Для того, чтобы сходился ряд

необходимо и достаточно, чтобы

;

(6). Для того, чтобы сходилось произведение

,

где и необходимо и достаточно, чтобы выполнялись два условия:

1) Существует номер такой, что при

2) .

Лемма 2.1. Если все коэффициенты ряда

целые числа, то он единственным образом представим в виде сходящегося (в топологии, порожденной метрикой (4)) произведения

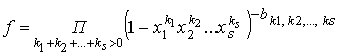, (7)

где порядок множителей соответствует порядку (2) на множестве , в котором все показатели также целые числа.

Доказательство. В силу критерия (6) любое произведение вида (7) сходится. Убедимся в существовании разложения (7) для ряда f.

Определим систему степенных рядов, расположенную в порядке (2), полагая

;

,

где - коэффициент разложения

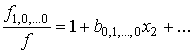и т.д.,

,

где - коэффициент разложения

;

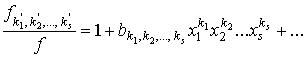индекс () непосредственно предшествует индексу в порядке (2) на множестве и т.д.

Если занумеровать ряды натуральными числами, располагая их в порядке, согласованном с (2):

,

то для любого номера будет выполняться неравенство

,

где биномиальный коэффициент. Из этого следует, что тогда и только тогда, когда . Учитывая это, получаем

,

так как

.

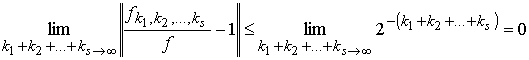Следовательно, в силу (6)

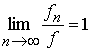и .

Из построения последовательности рядов следует, что все числа целые. Существование разложения (7) установлено, доказательство его единственности опускаем.

Лемма 2.1 доказана.

Обозначим через дифференциальный оператор в кольце , заданный формулой

,

,

. (8)

Оператор выражается через обычный оператор формального дифференцирования по переменной :

Если

,

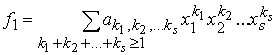то положим

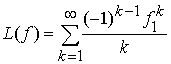, (9)

где ряд всегда сходится, так как

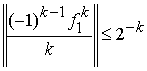
и, следовательно,

.

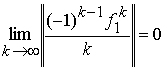Ряд (9) называется логарифмом ряда .

Лемма 2.2. Если ряд

сходится, то ряд

также сходится и выполняется равенство

.

Доказательство. Из определения видно, что

,

следовательно, этот оператор непрерывен. Так как

,

то

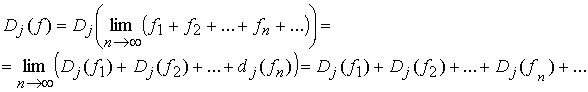
Лемма 2.2 доказана.

Лемма 2.3. Любой оператор вида

,

действующий в по формуле:

,

непрерывен (в топологии, порожденной метрикой (4)).

Доказательство опускаем.

Лемма 2.4. Имеет место равенство

(10)

Доказательство. Пусть . Тогда

.

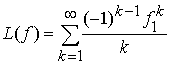По лемме 3

.

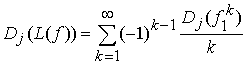Так как 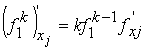, то

,

поэтому

.

Учитывая равенство

,

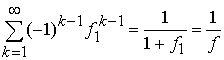убеждаемся в справедливости (10).

Лемма 2.5. Для любого оператора вида

выполняется равенство

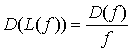. (11)

Доказательство опускаем.

Лемма 2.6. Если произведение

сходится, то сходится и ряд

и выполняется равенство

Доказательство. По условию . Так как

,

то ряд

сходится. Для любых справедливо представление

,

где

Имеем

.

Переходя в этом равенстве к пределу при , завершаем доказательство леммы 2.6.

Лемма 2.7. Пусть ряд , R , имеет целые коэффициенты,

,

(- оператор (8), ) и - какая-нибудь система взаимно простых натуральных чисел . Тогда при любом натуральном числе n коэффициенты ряда

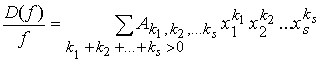
удовлетворяют сравнению

(12)

Доказательство. Фиксируем систему взаимно простых натуральных чисел и натуральное число n.

По лемме 2.1 ряд f представим в виде произведения (7). Взяв от обеих частей равенства частей (7) логарифм, получим равенство

, (13)

в котором ряд в силу леммы 4 сходится. Продифференцировав обе части (13), и учитывая (11), получим

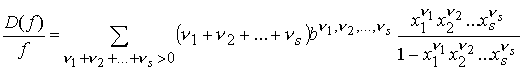(14)

Запишем (14) в виде

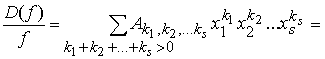
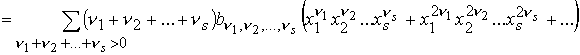(15)

У равных формальных рядов равны коэффициенты при одночлене . Напишем на основании (15) равенства коэффициентов рядов при всех одночленах вида

, (16)

где имеет следующий смысл: существует целое число l, удовлетворяющее системе равенств:

(17)

По условию найдутся целые числа , удовлетворяющие равенству

.

Тогда

; .

Пусть . Тогда из (17) получаем

.

Учитывая это, запишем (16) в виде:

(18)

Применяя известные формулы обращения систем вида (18) [4, т.2. VIII, N33], получаем

(19)

Из (19) при j = n следует

Лемма 2.7 доказана.

Лемма 2.8. Пусть ряд f, f имеет целые коэффициенты, ,

(- оператор (8), ) и - какая-нибудь система взаимно простых натуральных чисел .

Тогда при любом простом натуральном числе p коэффициенты ряда

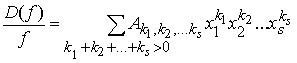
удовлетворяют сравнению

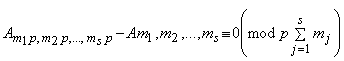_. (20)

Доказательство. Положим в (12) n = p. Получим равенство, равносильное (20). Следствие доказано.

Лемма 2.9. Пусть - целые неотрицательные числа с наибольшим общим делителем d. Тогда число

будет целым.

Доказательство. Обозначим через t наименьшее натуральное число при котором дробь

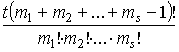
будет целым числом. При любом j, ,полиномиальный коэффициент

будет целым числом. Следовательно, при любом j, () число t будет делителем числа , а вместе с тем и делителем числа d.

Лемма 2.9 доказана.

Доказательство теоремы 1.

Применим лемму 2.7 к ряду . Имеем

,

Откуда находим

.

Следовательно,

. (21)

Подставляя (21) в (12), и разделив сравнение (12) на , завершаем доказательство теоремы 1.

Доказательство Следствия 1.

Полагая в (1): , , получим доказываемое сравнение.

Следствие 2. Пусть - взаимно простые натуральные числа.

Тогда при любых: целых а и простом числе р выполняется сравнение:

(22)

Доказательство. Если п = р – простое число, то оно имеет лишь два делителя: , . Учитывая, что , , из (1) получаем (22).

Следствие 2 доказано.

Следствие 3. Пусть - взаимно простые натуральные числа.

Тогда при любом натуральном n выполняется сравнение (23)

.

Доказательство. Сравнение (23) получается из (1) при a_j= 1 (j=1,2,…,s).

Следствие 4. Пусть - взаимно простые натуральные числа.

Тогда при любом простом р выполняется сравнение

(24)

Доказательство. Сравнение (24) получается из (22) при а = 1.

Следствие 5. При любых: натуральном s и простом p выполняется сравнение

(25)

Доказательство. Сравнение (25) получается из (24) при .

Следствие 6. При любом простом числе р

(26)

Доказательство. Сравнение (26) получается из (25) при s= 2.

Обобщением следствия 5 является

Следствие 7. При любых натуральных п и s выполняется сравнение

,

где - функция Мебиуса.

Доказательство опускаем.

Теорема 2. Пусть - корни уравнения с целыми коэффициентами

.

Тогда при любом натуральном п целые числа последовательности

,

удовлетворяют сравнению

; (27)

В частности, если р – простое число, то

. (28).

Доказательство получается применением леммы 2.7 к ряду

.

Отметим, что сравнение (28) известно как следствие аналога теоремы Ферма для алгебраических чисел.

Литература

[1] П. Кон. Универсальная алгебра. М.: Мир, 1968.

[2] Г. Грауэрт, Р. Реммерт. Аналитические локальные алгебры. М.: Наука, 1988.

[3] О.В. Мельников и др. Общая алгебра. Т.1. М.: Наука, 1990.

[4] Г. Полиа, Г. Сеге. Задачи и теоремы из анализа. Т.2. М.: Наука. 1978.

[5] Н.Ф. Мануилов. К теоремам Ферма и Эйлера. – Деп. ВИНИТИ. N2972-В92.

[6] Об одном применении формальных степенных рядов в теории делимости целых числе. СБ Полианалитические функции…, Смоленск, 1997.

RESEARCH OF PROPERTIES OF DIVISIBILITY POLYNOMIAL FACTORS AND DEGREES THE METHOD FORMAL SEDATE NUMBERS

Manuilov N. F.

In this work the method of formal sedate numbers proves some new results under the theory of divisibility of integers and consequences from them representing new and known properties of divisibility of polynomial factors and degrees.

Key words: an ascending power series, a differential operator, the ration of divisibility in a ring of integers, the ration of comparison, the greatest common divisor, a prime number.

Смоленский гуманитарный университет

Поступила в редакцию 15.04.2010.