Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 9. -
Вып. 2. - 2010. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/TITL-26.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/cont.htm
УДК 512
К теории идеалов в кольце
многочленов с целыми коэффициентами
Ó 2010
г. Мануилов Н.Ф.
Рассматривается кольцо
многочленов с целыми коэффициентами. Известно, что это кольцо факториально и
для него имеют смысл понятия: наибольшего общего делителя элементов, взаимной
простоты элементов и т.д. В работе
исследуются идеалы с двумя образующими в указанном кольце. Полученные результаты применимы для
построения систем счисления в полях алгебраических чисел, основанием которых
может быть любое, большее единицы по
модулю, алгебраическое число из соответствующего поля, а также для разработки
алгоритмов арифметических действий в таких системах.
Ключевые слова: кольцо, идеал в кольце,
образующие идеала, полином, нетерово кольцо, системы счисления с алгебраическими
основаниями.
Основным результатом настоящей заметки является
доказательство следующего предложения.
Теорема 1. Для любых взаимно простых многочленов f, g
[x] существуют взаимно простые многочлены u, v
[x], удовлетворяющие равенству
(1) 
,
где
делитель (в кольце
[x]) некоторого многочлена вида 
.
Доказательству предпосылается ряд вспомогательных предложений. Указываются
применения теоремы 1 к изучению строения идеалов в кольце рациональных функций
(теорема 2) и в теории алгебраических чисел (теорема 3).
Лемма 1. Пусть многочлены f, g
[x], взаимно просты. Тогда найдутся взаимно простые 
[x] и натуральное число m такие, что
(2) 
.
Доказательство.
Если f, g –
многочлены нулевой степени, то есть целые числа, то лемма 1 верна; если степень
только одного многочлена равна нулю – пусть это выполняется для g, - то,
полагая 
(знак выбирается так,
чтобы 
), получим 
, где 
взаимно просты и m>0.
Лемма 1 верна и в этом случае.
Пусть степень каждого из многочленов f, g не равна нулю. Так как f, g взаимно просты и в кольце Q[x] – в кольце многочленов с рациональными
коэффициентами, - то найдутся взаимно простые 
Q[x], удовлетворяющие равенству
(3) 
.
Пусть m наименьшее натуральное число, для которого 
[x]. Умножая (3) на m и полагая в полученном равенстве 
, приходим к (2).
Лемма 1 доказана.
Лемма 2. Пусть многочлены f, g
[x], взаимно просты. Тогда существуют 
[x], такие, что
(4) 
.
Доказательство.
По лемме 1 существуют 
[x] и 
такие, что
выполняется равенство (2). Не меняя общности утверждения можно полагать, что
число m взаимно просто хотя бы с одним из многочленов f или g. Предположим, что взаимно просты m и f. Пусть 
- каноническое разложение
числа m. Для 
найдутся многочлены 
[x], удовлетворяющие условию:
(5) 
.
Действительно, пусть 
, где 
первый коэффициент,
не делящийся на простое число 
и пусть 
- целые числа, для
которых 
.
Тогда (5) выполнится при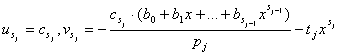 
.
Для 
возведем обе части
(5) в степень 
. Получаем
(6) 
.
Перемножая правые и левые части всех равенств (6),
находим
(7) 
, где 
.
Из (2) и (7) следует
(8) 
.
Полагая в (8) 
, получаем (4).
Лемма 2 доказана.
Лемма 3. Пусть многочлен 
и натуральное число m взаимно просты
(в кольце 
[x]). Тогда найдутся взаимно простые многочлены 
, удовлетворяющие равенству
(9) 
,
где
делитель (в кольце 
[x]) некоторого многочлена вида 
.
Доказательство.
Если m=0 или m=1, то лемма 3 верна.
Пусть m>1. По лемме 2 существуют многочлены 
[x], удовлетворяющие равенству
(10) 
, где 
.
Рациональная дробь 
в кольце формальных
степенных рядов разлагается в ряд с целыми коэффициентами:
(11) 
.
Для любого 
разделим 
на m с
остатком: 
.
Тогда (11) можно записать в виде: 
, откуда следует
(12) 
, где 
.
Из (12) находим: 
(13) 
.
Так как 
и 
единственным образом
определяются по числам 
и множество различных
векторов вида 
конечно (в силу условия:
), то последовательности 
будут почти периодическими:
периодическими, начиная с некоторого номера. Возможны два взаимоисключающих
случая (I и II).
I. Множества не равных нулю коэффициентов 
конечны. Тогда (12)
принимает вид:
(14) 
.
Из (10), (14) находим 
или
(15) 
.
Полагая в (15) 
, получаем (9).
В случае I лемма 3
верна.
II. По крайней мере одно из множеств 
не равных нулю коэффициентов в (12) бесконечно. Тогда при некотором натуральном l
,
откуда
следует
(16) 
.
Из (10), (16) выводим 
, откуда
(17) 
.
Пусть h – наибольший общий делитель многочленов 
.
Сокращая (17) на h и полагая после этого 
, 
, 
, получаем (9).
Лемма 3 доказана.
Доказательство теоремы 1.
Пусть многочлены
f, g
[x] взаимно просты. По лемме 1 существуют взаимно простые
[x] и натуральное число m, удовлетворяющие (2). Можно предполагать, что по крайней
мере, один из многочленов f или g взаимно
прост с числом m (в
кольце 
[x]). Предположим, что f и m взаимно просты. По лемме 3 существуют многочлены 
и многочлен 
- делитель некоторого
многочлена вида 
- удовлетворяющие
(9).
Из (2), (9) находим
(18) 
,
(19) 
.
Пусть 
наибольший общий
делитель многочленов 
.
Полагая в (19) 
получаем (1).
Теорема 1 доказана.
Приведем пример применения этой теоремы.
Пусть 
и задается условием:
(20) 
|
- делитель многочлена вида 
.
Множество S мультипликативно замкнуто в 
[x], [1, стр.49]. Действительно, 1
; если 
делитель многочлена 
, 
делитель многочлена 
, то 
делитель многочлена 
.
Следовательно, множество дробей
(21) 
| 
с
обычными операциями сложения и умножения является кольцом, [1, стр.50].
Теорема 2. Кольцо 
есть кольцо главных
идеалов.
Доказательство.Так как кольцо 
[x] нетерово, [1, стр.100], то кольцо 
также нетерово, [1,
стр.99], то есть любой его идеал конечно порожден.
Пусть I некоторый идеал кольца 
.
Тогда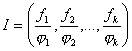 
, где 
.
Кольцо 
факториально,
следовательно, существуют многочлены 
такие, что
(22) 
(
)
и
многочлены 
взаимно просты в
совокупности. Из (22) вытекает, что имеет место включение идеалов.
(23) 
.
В кольце 
наибольший общий
делитель многочленов 
равен единице, и,
следовательно, при некоторых 
(
) выполняется равенство
(24) 
.
Пусть m наименьшее натуральное число, при котором: 
. Умножая (24) на mh, получим 
, откуда видно, что 
.
Не меняя общности утверждения можно полагать, что
число m взаимно просто, по крайней мере, с одним из многочленов
. Предположим, что 
и m взаимно
просты. Тогда по теореме 1 при некоторых 
и 
(25) 
.
Умножая (25) на h и учитывая, что 
, приходим к выводу, что 
.
Но тогда 
и имеет место
включение идеалов 
. Итак, установлено, что 
, следовательно, 
, I – главный идеал.
Теорема 2 доказана.
Теорема 3. Пусть знаменатель дроби 
взаимно прост с h (
) и 
- какой-нибудь корень
многочлена h, модуль которого не равен единице. Тогда существует
конечное множество L целых чисел (зависящее, вообще говоря, от 
) такое, что алгебраическое число 
представляется в виде
суммы ряда 
(
),
где
; последовательность (
) почти периодическая; 
1, если 
, и 
-1, если 
.
Доказательство теоремы 3 опускаем. Вопросы, затронутые
в этом предложении в случае, когда h неприводимый многочлен и все его корни по модулю
больше единицы, подробно обсуждаются в
[3].
ЛИТЕРАТУРА
[1]. М.Атья, И.Макдональд. Введение в коммутативную
алгебру. М.: Мир, 1972.
[2]. С.Ленг. Алгебра. М.: Мир, 1968.
[3]. Н.Ф.Мануилов. Алгоритмическая арифметика в полях
алгебраических чисел. Деп. в УкрНИИНТИ, № 1537-Ук88.
To the theory of ideals in a ring of polynomials with
the whole factors
Manuilov N. F.
The
ring of polynomials with the whole factors is considered. It is known, that
this ring factorial and for it concepts make sense: the greatest general
divider of elements, mutual simplicity of elements, etc. In work ideals with
two forming in the specified ring are investigated. The received results to
apply for construction of number systems in fields of algebraic numbers which
basis can be any, greater units on the module, algebraic number from the
corresponding field, and also for development of algorithms of arithmetic
actions in such systems.
Key words: a ring, an ideal
in a ring, forming ideal, a polynomial, a Noetherian ring, number systems with
the algebraic foundation.
Смоленский
гуманитарный университет
Поступила в
редакцию 15.04.2010.