Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 9. -
Вып. 2. - 2010. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/TITL-26.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/cont.htm
УДК
681.3.001.57
СПОСОБ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ МОДЕЛИ АВТОРЕГРЕССИИ ПРОИНТЕГРИРОВАННОГО
СКОЛЬЗЯЩЕГО СРЕДНЕГО
Ó 2010 г. Волосенков А. В.
Рассматривается задача построения
АРПСС модели временных рядов. Предложенный метод для определения параметров
модели для будущего прогноз базируется на основных характеристиках временных
рядов. Метод позволяет упростить задачу нахождения оптимальной модели на
приемлемом уровне погрешности результата.
Ключевые слова: процедура, параметры,
информация, математическая модель, процесс.
Процедуры оценки параметров
и прогнозирования, зачастую предполагают, что математическая модель процесса
известна. Однако в реальных данных часто нет отчетливо выраженных регулярных
составляющих. Отдельные наблюдения содержат значительную ошибку, тогда как
необходимо не только выделить регулярные компоненты, но также построить
прогноз. Метод авторегрессии проинтегрированного скользящего среднего (АРПСС),
разработанный Боксом и Дженкинсом [1], позволяет это сделать. Данный метод
чрезвычайно популярен во многих приложениях, и практика подтвердила его
мощность и гибкость. В то же время следует отметить сложность определения
параметров модели АРПСС. Хотя метод АРПСС дает удовлетворительные результаты,
они зависят от квалификации пользователя. Важным этапом в построении прогноза
на основе АРПСС модели является определение ее параметров.
Основными инструментами
идентификации порядка АРПСС модели являются графики автокорреляционной функции ![]() (АКФ) и частной автокорреляционная функция
(АКФ) и частной автокорреляционная функция ![]() (ЧАКФ).
(ЧАКФ).
Одно из главных отличий
последовательности наблюдений, образующих временной ряд, от случайной выборки
заключается в том, что члены временного ряда являются статистически
взаимозависимыми. Степень тесноты статистической связи между двумя случайными
величинами может быть измерена парным коэффициентом корреляции. Поскольку
коэффициент измеряет корреляцию,
существующую между членами одного и того же временного ряда, его принято
называть коэффициентом автокорреляции. При анализе изменения величины ![]() в
зависимости от значения t принято говорить об автокорреляционной
функции
в
зависимости от значения t принято говорить об автокорреляционной
функции ![]() . График автокорреляционной функции иногда называют коррелограммой.
Автокорреляционная функция (в отличие от автоковариационной) безразмерна, т.е.
не зависит от масштаба измерения анализируемого временного ряда. Ее значения,
по определению, могут колебаться от -1 до +1.
. График автокорреляционной функции иногда называют коррелограммой.
Автокорреляционная функция (в отличие от автоковариационной) безразмерна, т.е.
не зависит от масштаба измерения анализируемого временного ряда. Ее значения,
по определению, могут колебаться от -1 до +1.
Значение автокорреляционной
функции определяется формулой [2]:
![]()
Существуют общие характерные
особенности, отличающие поведение автокорреляционной функции стационарного временного
ряда. Другими словами, можно описать в общих чертах схематичный вид
коррелограммы стационарного временного ряда. Это обусловлено следующим общим
соображением: очевидно, чем больше разнесены во времени члены временного ряда ![]() и
и ![]() , тем слабее взаимосвязь этих членов и, соответственно, тем меньше
должно быть по абсолютной величине значение
, тем слабее взаимосвязь этих членов и, соответственно, тем меньше
должно быть по абсолютной величине значение ![]() . При этом в ряде случаев существует такое пороговое значение
. При этом в ряде случаев существует такое пороговое значение ![]() , начиная с которого все значения
будут тождественно равны нулю.
, начиная с которого все значения
будут тождественно равны нулю.
С помощью частной
автокорреляционной функции ![]() реализуется идея измерения
автокорреляции, существующей между разделенными t тактами времени членами временного ряда
реализуется идея измерения
автокорреляции, существующей между разделенными t тактами времени членами временного ряда ![]() и
и ![]() , при устраненном опосредованном влиянии на эту взаимозависимость всех
промежуточных членов этого временного ряда. Частная автокорреляция 1-го порядка
может быть подсчитана с использованием соотношения:
, при устраненном опосредованном влиянии на эту взаимозависимость всех
промежуточных членов этого временного ряда. Частная автокорреляция 1-го порядка
может быть подсчитана с использованием соотношения:
![]()
Частные автокорреляции более
высоких порядков могут быть подсчитаны аналогичным образом по элементам общей
корреляционной матрицы ![]() , в которой
, в которой ![]() . Так, например, частная автокорреляция k-го порядка определяется по
формуле [2]:
. Так, например, частная автокорреляция k-го порядка определяется по
формуле [2]:
![]()
![]()
Полученные таким образом
частные автокорреляции ![]() ,… можно нанести на график, в котором роль абсциссы выполняет величина
сдвига t. Знание автокорреляционных
функций
,… можно нанести на график, в котором роль абсциссы выполняет величина
сдвига t. Знание автокорреляционных
функций ![]() и
и ![]() оказывает существенную помощь в
решении задачи подбора и идентификации модели анализируемого временного ряда.
оказывает существенную помощь в
решении задачи подбора и идентификации модели анализируемого временного ряда.
Это решение не является
простым и требуется основательно поэкспериментировать с альтернативными
моделями. С целью уменьшения сложности вычислений предлагается следующий способ
определения параметров модели АРПСС. Большинство встречающихся на практике
временных рядов можно с достаточной степенью точности аппроксимировать одной из
5 основных моделей, которые можно идентифицировать по виду автокорреляционной
(АКФ) и частной автокорреляционной функции (ЧАКФ). Отметим, что число параметров
каждого вида невелико (меньше 2), поэтому нетрудно проверить альтернативные
модели.
1. Один параметр (p): АКФ -
экспоненциально убывает; ЧАКФ - имеет резко выделяющееся значение для лага 1,
нет корреляций на других лагах.
2. Два параметра авторегрессии
(p): АКФ имеет форму синусоиды или экспоненциально убывает; ЧАКФ имеет резко
выделяющиеся значения на лагах 1, 2, нет корреляций на других лагах.
3. Один параметр скользящего
среднего (q): АКФ имеет резко выделяющееся значение на лаге 1, нет корреляций
на других лагах. ЧАКФ экспоненциально убывает.
4. Два параметра скользящего
среднего (q): АКФ имеет резко выделяющиеся значения на лагах 1, 2, нет
корреляций на других лагах. ЧАКФ имеет форму синусоиды или экспоненциально
убывает.
5. Один параметр авторегрессии
(p) и один параметр скользящего среднего (q): АКФ экспоненциально убывает с
лага 1; ЧАКФ - экспоненциально убывает с лага 1.
Общие рекомендации относительно выбора обычных параметров (с помощью АКФ и ЧАКФ) полностью применимы к сезонным моделям. Основное отличие состоит в том, что в сезонных рядах АКФ и ЧАКФ имеют существенные значения на лагах, кратных сезонному лагу (в дополнении к характерному поведению этих функций, описывающих регулярную компоненту АРПСС).
Стоит отметить, что в
процессе определения параметров АРПСС подели,
параллельно определяется наличие сезонности в рассматриваемом временном
ряде. Рассмотрим применение данного способа для анализа показателя инвестиций в
основной капитал Российской Федерации
за период с января 2005 года по февраль 2010 года. На рис. 1 представлен
исходный временной ряд с выделенным трендом.
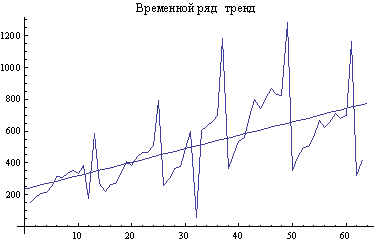
Рис. 1. Инвестиции в основной капитал РФ
Применительно к ряду, с предварительно исключенным
трендом, получим графики автокорреляционной и частной автокорреляционной
функций, изображенные на рис. 2 и 3:
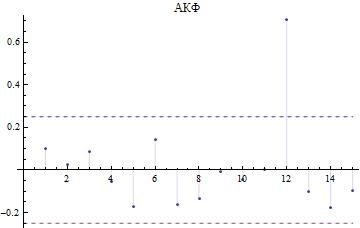
Рис. 2.
График автокорреляционной функции
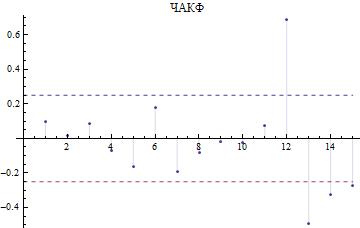
Рис. 3. График частной
автокорреляционной функции
Значения АКФ и ЧАКФ на 12 лаге, говорят о ярковыраженной сезонности рассматриваемого ряда (период составляет 12 месяцев), что полностью соответствует реальным показателям инвестиций в основной капитал.
Литература
1. Бокс Дж., Дженкинс Г.
Анализ временных рядов. Прогноз и управление. - М. Мир, 1974. - Вып. 1, 2.
2. Лукашин Ю.П. Адаптивные
методы краткосрочного прогнозирования временных рядов: Учеб пособие. – М.
Финансы и статистика, 2003 – 416 с.
METHOD FOR DETERMINING PARAMETERS OF AUTOREGRESSIVE
INTEGRATED MOVING AVERAGE MODEL
Volosenkov
A.V.
The problem of constructing ARIMA models for
time series is considered. The proposed method for determining the parameters
of the model for future prediction based on the basic characteristics of time
series. The method allows to simplify the task of finding the optimal model
with acceptably level of error result.
Key words: procedure, parametres, the information,
mathematical model, process.
Филиал ГОУВПО Московский
энергетический институт
(Технический университет) в
г. Смоленске
Поступила в редакцию
28.05.2010.