Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 9. -
Вып. 2. - 2010. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/TITL-26.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-26-html/cont.htm
УДК 621.39:621.391.82
ГОМОМОРФНО-КОРРЕЛЯЦИОННАЯ
ОБРАБОТКА КОДОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ СВЕРХШИРОКОПОЛОСНЫХ ИМПУЛЬСОВ ПРИ
ПОЗИЦИОННОМ КОДИРОВАНИИ
Ó
2010 г. Жбанов И. Л., Силаев Н. В.
В данной статье рассмотрена проблема выделения информации в
сверхширокополосных системах связи при синхронизации моментов приема и передачи
данных. Предложен новый подход выделения информации
из закодированной последовательности сверхширокополосных импульсов при позиционном
кодировании. Путем математического моделирования исследовано влияние
различных факторов на работоспособность и характеристики метода.
Ключевые слова: обработка сигналов,
сверхширокополосные импульсы, спектр, информация
В
настоящее время в современных сверхширокополосных (СШП) системах передачи
данных (СПД) [1–6] выделение информации возможно лишь при жесткой синхронизации
моментов приема и передачи информации. Для достижения синхронной работы приемника
и передатчика используют дополнительные узкополосные или сверхширокополосные сигналы
[7], что повышает стоимость изготовления соответствующей СПД.
В статье рассмотрен новый подход к выделению информации для СШП
СПД, не использующий синхронизацию моментов приема и передачи информации.
Позиционное кодирование заключается в
использовании в качестве основных носителей информации импульсов наносекундной
длительности, описываемых первой производной гауссовой функции [3]
,
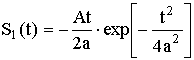где А – амплитуда импульса; a – величина, характеризующая
половину длительности импульса на уровне 0,707.
Применяется периодическая последовательность гауссовых
импульсов, состоящая из расположенных в определенном порядке «опорных» и
«центральных» импульсов. Причем «опорные» импульсы отличаются от «центральных»
тем, что их период следования T постоянен. В результате вся
информация о кодировании будет заключена во временном положении «центрального»
СШП импульса относительно «опорных» (рис. 1).
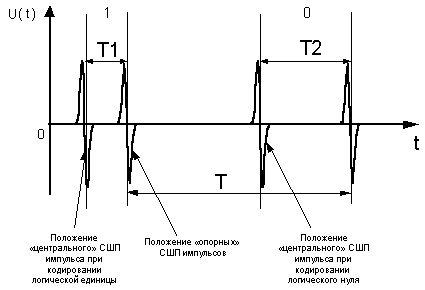
Рис. 1. Кодирование логического нуля
либо единицы
При данном подходе к
кодированию информации должно выполнятся условие 
, где 
, 
– задержки между «опорными» и «центральными» импульсами; Т –
период следования «опорных» СШП импульсов.
Набор нескольких бит
информации представляет собой некоторое сообщение (рис. 2), именуемое
кодограммой, которая излучается источником СШП сигналов, а затем принимается в
другой точке пространства.
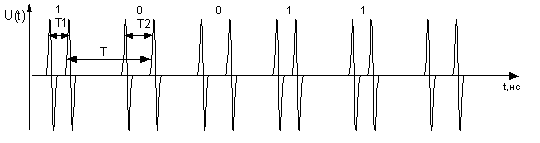
Рис. 2. Набор нескольких бит информации, представляющие собой
полезное сообщение
(кодограмму)
После приема и усиления
кодограммы, ее импульсы интегрирующею RC–цепь. В результате
интегрирования формируется последовательность однополярных сверхширокополосных
импульсов, имеющих аналитическое описание вида
(1)
Интегрирование необходимо
для последующего расширения импульсов и их оцифровки, так как при форме
импульса, отличной от однополярной, расширение приводит к искажению формы сигналов. Расширение импульсов
необходимо для качественной оцифровки сигнала аналого-цифровым преобразователем
(АЦП) [8]. На первом этапе расширения СШП сигнал делится по мощности на K частей
[9]. Затем каждая из этих частей задерживается на время 
, вычисляемое по формуле
,
где 
– номер выхода делителя; 
– необходимая длительность одиночного СШП импульса
после интегрирования; K – количество плеч делителя
по мощности.
Требуемое количество линий
задержки Н связано с числом плеч делителя соотношением
. Затем все задержанные части сигнала складывают между собой
по мощности.
Параметр K
определяется длительностью СШП импульсов после интегрирования и необходимой
длительностью СШП импульсов для АЦП и находится из неравенства
,
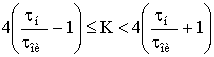где
– минимальная
необходимая длительность СШП
импульса, которую нужно иметь для достоверного восстановления формы сигнала после
аналого-цифрового преобразования;
– длительность СШП импульсов после интегрирования;
– частота дискретизации АЦП.
Сформированный
набор цифровых данных, описывающий сигнал, поступает в ЭВМ, где осуществляется
его разделение на массивы, соответствующие значению оцифрованного сигнала в пределах
интервалов длительностью
∆. Величина ∆ вычисляется по формуле 
, где 
– длительность одного
оцифрованного растянутого импульса.
Деление на интервалы 
происходит постоянно
и независимо от времени прихода оцифрованной последовательности импульсов.
Начало очередного z-го интервала 
должно отличатся от
начала предыдущего временного интервала
на величину 
. Операцию разделения на интервалы производят до тех пор,
пока в интервале 
не окажутся первые
два импульса принимаемой кодограммы (эпюра а рис. 3).
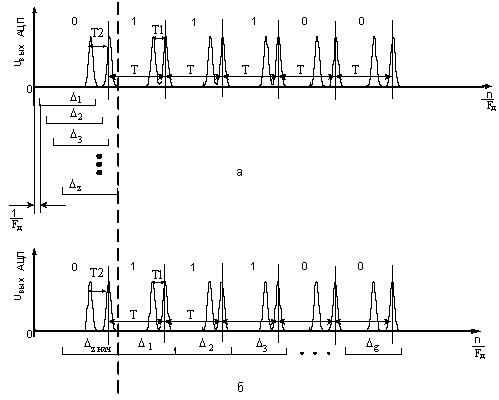
Рис. 3. Деление оцифрованной кодограммы на массивы данных
Значение исходного
оцифрованного сигнала в пределах каждого
интервала ∆ подвергается кепстральной обработке [10]. Согласно
предлагаемому способу при помощи дискретного прямого преобразования Фурье (ППФ)
вычисляется спектр для значений оцифрованного сигнала, ограниченного интервалом
∆, причем для каждого z-го
интервала в отдельности. При этом используется выражение
,
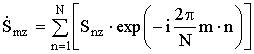где n – номер отчета во временной
области, m – номер отчета в частотной области; 
– значение
комплексной амплитуды m-го отсчета спектра оцифрованного
сигнала; 
– значение амплитуды n-го по
номеру отсчета, находящегося в интервале 
.
Затем рассчитывается
логарифм квадрата модуля каждого m-го спектрального значения
оцифрованного сигнала в каждом z-м интервале по формуле 
рис.4.
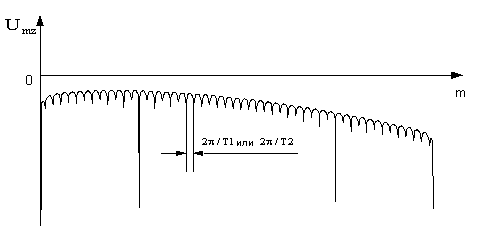
Рис. 4. Логарифм квадрата
модуля каждого m-го спектрального значения
оцифрованного сигнала
Полученные данные массива 
подвергают пакетному
вейвлет разложению на коэффициенты аппроксимации и детализации до четвертого
уровня [11], а также обратному восстановлению с учетом лишь коэффициентов
детализации, при помощи матричной системы MATLAB. В результате, будет получен новый массив данных 
(рис. 5). Данная
операция необходима, для дальнейшего определения автокорреляционной функции.
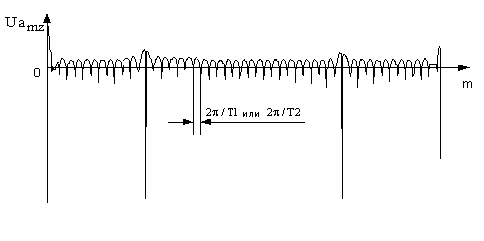
Рис. 5. Результат вейвлет
преобразования массива 
От полученного результата
находят автокорреляционную функцию (рис. 6) по формуле
,
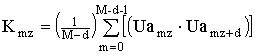где M – число элементов в массиве
, равное N; d – целое число составляющее
20% от N.
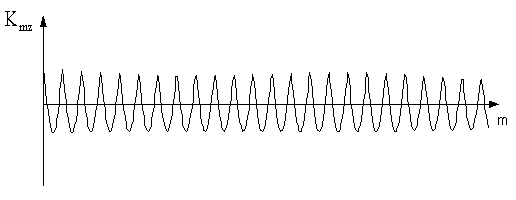
Рис. 6. Автокорреляционная
функция массива 
От полученного результата 
вычисляют дискретное
обратное преобразование по формуле
.
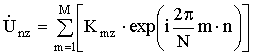После этого вычисляют
значение модуля для каждого m-го отсчета соответствующего
z-го основного массива. В результате получают z-й кепстральный массив, состоящий
из элементов 
, который представляет собой
кепстр z-го пробного массива. Для декодирования информации
каждый кепстральный массив разбивают на два массива 
, 
. При этом массив 
z-го
кепстрального массива включает в себя значения кепстра с номерами от 
до 
, где 
; 
; 
– функция округления в сторону меньшего целого числа. Массив 
z-го
кепстрального массива включает в себя
значения кепстра с номерами от 
до 
, где
; 
.
В последующем используют
заранее полученное максимальное значение
амплитуды кепстрального отклика в массиве 
или 
при отсутствии
помех, записанного в ЭВМ, умножают полученное максимальное значение кепстра на
0,7 и принимают результат в качестве порогового значения 
для z-го
кепстрального массива. Сравнивают величину 
с каждым
значением соответствующего z-го кепстрального массива.
При превышении порога 
значениями
кепстра только в массиве 
или при превышении
порога 
значениями
кепстра только в массиве 
и отсутствии
превышения порога 
в массиве 
принимают решение
о наличии в z-м интервале 
ровно двух импульсов.
Затем формируют G новых рабочих массивов данных из генерального массива
данных D.
В процессе последовательной проверки выполнения этих
условий для каждого интервала 
фиксируется исходный
интервал 
, в котором определено наличие двух первых импульсов. С
учетом этого положение следующих интервалов
смещается на величину
(эпюра б рисунок 3). При таких
смещениях каждый последующий g-й интервал
будет включать
ровно два оцифрованных импульса, определяющих передачу логического «нуля» либо
«единицы». Подвергая данные, описывающие оцифрованный сигнал в каждом g-м
интервале, кепстральной обработке, принимают решение о приеме логического нуля
или единицы. Для декодирования информации каждый кепстральный массив разбивают
на два массива 
, 
. При этом массив
g-го
кепстрального массива включает в себя значения кепстра от 
до 
. Массив 
g-го
кепстрального массива включает в себя значения кепстра от 
до 
. В последующем используют заранее полученное максимальное
значение амплитуды кепстрального
отклика в массиве 
или 
при отсутствии
помех, записанного в ЭВМ. Умножают полученное
максимальное значение кепстра на 0,7 и принимают результат в качестве
порогового значения 
для g-го
кепстрального массива. Cравнивают величину 
с каждым значением
соответствующего g-го кепстрального массива. При превышении порога 
значениями
кепстра только в массиве 
принимают решение
о наличии в данном g-м интервале 
закодированной
логической единицы (рис. 7).
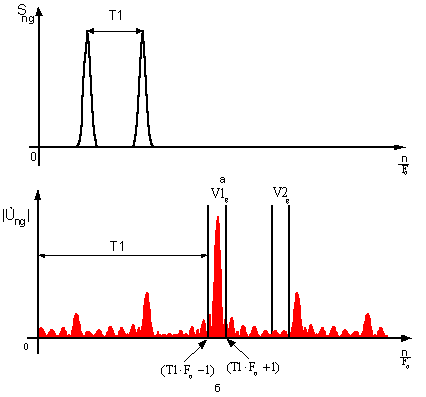
Рис. 7. Кепстр,
соответствующий положению логической единицы
в g-м интервале
При превышении порога 
значениями
кепстра в массиве 
принимают решение
о наличии в данном g-м интервале 
закодированного
логического нуля (рис. 8).
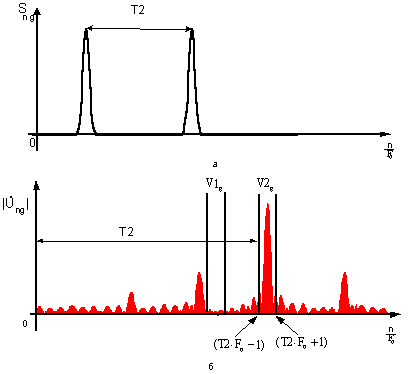
Рис. 8.
Кепстр, соответствующий положению логического
нуля в g-м
интервале
Выделенная информация из
первого кепстрального массива соответствует первому биту информации принятой
кодограммы. Информация из второго
кепстрального массива соответствует второму биту информации принятой
кодограммы. А информация из g-го кепстрального массива
соответствует g-му биту информации принятой кодограммы. В последующем
создают результирующий массив, представляющий собой расшифрованную кодограмму.
В его элементы записывают последовательно информацию из каждого g-го
кепстрального массива. При отсутствии превышения порога 
значениями
кепстра в установленных массивах 
и 
принимают
решение об окончании приема кодограммы, после чего с объекта Y на
объект X посылают запросный сигнал, свидетельствующий о готовности объекта Y к
приему следующей кодограммы.
Так как дискретный сигнал в
каждом интервале представляет собой сумму двух оцифрованных импульсов почти
одинаковой формы и задержанных
относительно друг друга на время Т1 при кодировании логической «единицы»
или на время Т2 при кодировании логического «нуля», то наложение сдвинутых
копий на исходный импульс создает эффект модуляции спектра энергии дискретного
сигнала по некоторому закону. При этом период модуляции будет равен 
или 
. При логарифмировании спектра энергии дискретного сигнала
можно перейти от произведения спектра одиночного оцифрованного импульса и
закона модуляции спектра сигнала к сумме их логарифмов. Модуль от значений,
полученных с выхода блока обратного преобразования Фурье, позволит получить
суммарный дискретный сигнал, именуемый кепстром. В нем закону модуляции энергетического
спектра дискретного сигнала с периодом 
или 
соответствует импульс
на кепстральной оси времени с максимумом в момент времени Т1 или Т2. Таким
образом, кепстальная обработка позволяет выявить период повторения закона
модуляции энергетического спектра дискретного сигнала, который равен нулю при
наличии одного оцифрованного импульса в интервале 
, равен 
(
) при наличии двух оцифрованных импульсов, несущих информацию
о логическом «нуле» («единице»).
Работоспособность
предложенного асинхронно-кепстрального метода
извлечения информации из закодированной последовательности коротких
сверхширокополосных импульсов проверена на математической модели (ММ) системы передачи данных (СПД), которая
включала ММ кодовой последовательности сверхширокополосных импульсов, передающей
антенны, канала связи, приемной антенны
и математическую модель предлагаемого
метода обработки СШП импульсов. Для получения ММ приемной и передающей антенны использовалась
лабораторная установка, состоящая из генератора СШП импульсов TMГ075045ВО01,
стробоскопического осциллографа ТМР8220 и двух идентичных СШП рупорных антенн.
На основе измеренных с
помощью стробоскопического осциллографа параметров СШП сигналов на выходе
генератора и приемной антенны осуществлялся расчет импульсных характеристик
приемной и передающей антенн. При этом приемная и передающая антенна
рассматривались в виде четырехполюсников с одинаковыми коэффициентами передачи.
На основе теории четырехполюсников
находились импульсные характеристики
приемной и передающей антенн, используемые затем в ММ СПД. Предложенные ММ позволяли
исследовать работоспособность предложенного метода в условиях помех различной интенсивности.
Для этого в ММ канала связи осуществлялось сложение кодовой последовательности
СШП импульсов с шумом, распределенным по нормальному закону с нулевым
математическим ожиданием и различными дисперсиями.
Результаты выделения
информации при различном отношении сигнал-шум Q на входе приемной антенны,
представлены в таблице 1.
Таблица 1
Зависимость вероятности верного выделения
информации предлагаемым методом от отношения
сигнал-шум на входе приемной антенны
|
Отношение сигнал/шум, Q [дБ] |
1 |
6 |
12 |
18 |
24 |
32 |
40 |
|
Вероятность верного выделения информации |
0,664 |
0,772 |
0,823 |
0,921 |
0,959 |
0,981 |
0,999 |
Анализ результатов
моделирования показал, что предложенный
подход работоспособен и имеет следующие достоинства: обеспечение асинхронной
работы приемника и передатчика; отсутствие задержки приема сообщения; высокая
скрытность передачи данных за счет использования СШП импульсов в качестве
основных носителей информации; возможность передачи информации со скоростью до
100 Мбит/с при периоде следования «опорных» СШП импульсов десятки наносекунд.
Предложенный подход может
найти применение в перспективных высокоскоростных, скрытных системах передачи
данных как гражданского, так и военного назначения. К ограничениям подхода
можно отнести необходимость дублирования передаваемого сообщения для повышения
вероятности достоверного выделения информации.
литература
1.
Шахнович И.В. Современные технологии беспроводной связи.– М.: Техносфера, 2006. 166 c.
2.
Скосырев В.Н. Особенности и свойства сверхкороткоимпульсной локации. – Муром,
2003. 91 c.
3. Иммореев И.Я. Сверхширокополосные радары:
новые возможности, необычные проблемы, системные особенности/Вестник
МГТУ,1998.№4. 56 c.
4. Siwiak K., Withington P. Ultrawideband
radios set to play // Electronics times, 2001. February 26.
5. Fontana R.J. Recent
System Applications of Short-Pulse Ultra-Wideband (UWB) Technology // IEEE
Transactions on microwave theory and techniques, vol. 52. № 9.
6. Immoreev I.J., Sudakov A.A. Ultra-Wideband
Interference Resistant System for Secure Radio Communication with High Data
Rate, ICCSC 02, St. Petersburg, Russian Federation, 2002.
7. Патент 2315424 (РФ). Система связи с высокой скоростью передачи информации сверхширокополосными
сигналами. МПК7 H04B1/69,
H04L5/26. Бондаренко В.В., Кыштымов С.Г. Заявка № 2006119887 от 6.06.2006. Опубл. 20.01.2008 г.
8. http://www.lecroyscope.ru/index.php?page=x-stream/Технология потоковой
обработки сигнала LeCroy X-Stream.
9. Справочник по элементам полосковой техники / Под ред. О.И. Мазепова, Связь, 1979. 179 с.
10.
Гоноровский И.С. Радиотехнические цепи и сигналы.– М.: Радио и связь, 1986. 477
с.
11.
Смоленцев Н.К., Основы теории вейвлетов. Вейвлеты в MATLAB: Издание третье. – М.:
Прикладная математика, 2008. 126
с.
HOMOMORPHICALLY-CORRELATION PROCESSING OF A CODE
SEQUENCE OF SUPERBROADBAND PULSES AT ITEM CODING
Zhbanov I. L., Silaev N. V.
The problem of getting of the information in superbroadband systems of
transfer of transmission without synchronization of reception moment and data
transmission is considered. The new approach of formation and processing of
pulse sequences with position coding of superbroadband pulses for high-speed
systems of data transmission is is offered. The working capacity and the characteristics
of the method in noises of different intensity are investigated by the math
modeling.
Key words: processing of signals, superbroadband
impulses, a spectrum, the information.
Военная академия войсковой ПВО Вооруженных Сил Российской Федерации
имени Маршала
Советского Союза А.М. Василевского
(ВА ВПВО ВС РФ)
Поступила в редакцию
28.05.2010.