Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 9. -
Вып. 3. - 2010. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-27-html/TITL-27.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-27-html/cont.htm
УДК 004.272.45
РАЗРАБОТКА И ИСПОЛЬЗОВАНИЕ ТЕСТОВОГО ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ДЛЯ
ИССЛЕДОВАНИЯ ОСОБЕННОСТЕЙ РЕШЕНИЯ ЗАДАЧ НА КЛАСТЕРЕ МОСКОВСКОГО ЭНЕРГЕТИЧЕСКОГО
ИНСТИТУТА
Ó
2010 г. Иванов М. Е.
Работа посвящена рассмотрению вычислительных кластеров как одно из
крупнейших классов высокопроизводительных систем, исследованию особенностей
кластерных вычислительных систем на примере вычислительно кластера Московского
Энергетического Института, а также вопросам о целесообразности оптимизации
существующих для них алгоритмов.
Ключевые слова: параллельные вычисления, кластер, параллельные алгоритмы.
Введение
Широкому
распространению многопроцессорных вычислительных систем способствовало развитие
коммуникационных технологий: появление высокоскоростного сетевого оборудования
и специального программного обеспечения, реализующего механизм передачи
сообщений над стандартными сетевыми протоколами, сделало кластерные технологии
общедоступными.
Кластерные
вычислительные системы можно определить как группу объединенных компьютеров,
управляемых и используемых как единое целое. Они могут быть одно- или
мультипроцессорными.
Кластер строится на базе
массово выпускаемых компонентов и состоит из вычислительных узлов, объединенных
высокопроизводительной системной сетью [1].
Кластерная архитектура
решений предоставляет пользователям вычислительных систем с суперкомпьютерным
уровнем производительности ряд существенных преимуществ:
- наиболее выгодное
соотношение "цена/производительность";
- практически неограниченные
возможности расширения: производительность кластера можно увеличить путем простого
добавления стандартных вычислительных узлов;
- высокая отказоустойчивость:
при выходе из строя вычислительного узла его легко заменить без остановки
системы;
- простота обслуживания.
Несмотря на выше
перечисленные достоинства, в развитии современных кластерных вычислительных
систем можно выделить такие недостатки, как задержки разработки и принятия
общих стандартов, большая доля нестандартных и закрытых разработок различных
фирм, затрудняющих их совместное использование, трудности управления одновременным
доступом к файлам, сложности с управлением конфигурацией, настройкой, развёртыванием,
оповещениями серверов о сбоях [2].
Ученые и
квалифицированные специалисты во многих областях науки и техники сталкиваются с
задачами, требующими для своего решения значительных вычислительных ресурсов.
Это обуславливает необходимость распараллеливания вычислительных алгоритмов. К решению данной задачи существует
множество подходов. Однако нахождение параллельного варианта алгоритма само по
себе не дает оптимального времени решения задачи на кластерных системах.
Значительную роль играют архитектурные особенности кластерной системы, в
частности, коммутационные связи между
вычислительными устройствами.
Данная работа
посвящена исследованию особенностей кластерной вычислительной системы с
использованием специального разработанного тестового программного обеспечения.
1. Краткое описание кластера Московского
энергетического института
В качестве исследуемого кластера в данной работе
используется вычислительный кластер Московского энергетического
института (МЭИ).
Вычислительный кластер МЭИ [3] имеет в своем
составе 66 ядер (32 двухъядерных вычислительных процессора и два одноядерных
управляющих процессора) пиковой производительностью 281 Гигафлоп (см. рис. 1).
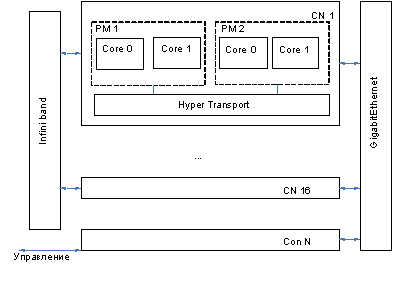
Рис. 1. Обобщенная структура вычислительного
кластера МЭИ
В состав кластера входят 16
вычислительных (computing node – CN) и один управляющий узел (control node
Con N); каждый из CN выполнен на двух двухядерных процессорах AMD Opteron 275,
а Con N на двух одноядерных процессорах AMD Opteron 254. Каждый CN имеет в
своем составе общую память емкостью 4 ГБ и дисковую память HDD емкостью
2*73Гбайт. Con N имеет общую память емкостью 8 Гбайт и дисковую – 73Гбайт.
Связь между процессорами CN
осуществляется с помощью локальной сети AMD HyperTransport, связь между
узлами - с помощью системной сети
InfiniBand, связь с внешним миром осуществляется с помощью вспомогательной сети
Gigabit Ethernet. В качестве операционной системы выступает ОС SUSE Linux
Enterprise Server 10.
Наиболее распространенной
технологией, применяемой для программирования многопроцессорных систем с
распределенной памятью, к которым относится кластер МЭИ, является использование
параллельных процессов, взаимодействующих с помощью передачи сообщений.
Основным средством разработки программ в данной парадигме является MPI (Message-Passing interface).
В состав среды программирования MPI входит библиотека с
интерфейсом для языков С и С++, а также средства для запуска и сборки параллельного
приложения [4].
2.Тестовое
программное обеспечение, разработанное для исследования кластера МЭИ
Для исследования
особенностей выполнения задач на кластере МЭИ были использованы две программы –
Метод прямоугольников (МП) и Передача массива от одного ко всем (ПМОВ).
Программа МП реализует
параллельный алгоритм решения задачи численного интегрирования методом
прямоугольников [4]. Отрезок интегрирования разбивается на некоторое количество
интервалов. На каждом интервале площадь под кривой подынтегральной функции f(x)
аппроксимируется к площади прямоугольника с основанием данного интервала и
высотой, равной значению функции f(x) в середине интервала.
Параллельная реализация данного алгоритма заключается в одновременном
выполнении вычислений на разных участках интервала интегрирования. Реализована
программа для вычисления интеграла функции y=4/(1+x2) в интервале [0, 1] с
разбиением на 109 участков. Текст программы МП на языке C с
использованием библиотеки MPI представлен ниже.
#include <mpi.h>
#include <stdio.h>
#include <time.h>
time_t realtime(void);
double f(double x)
{
return 4./(1 + x * x);
}
int main(int argc, char* argv[])
{
int r;
int p;
int i;
double sum;
double h;
MPI_Status st;
double t_calc;
time_t t_init_b,t_init_e;
int n = 1000000000;
double a = 0.0;
double b = 1.0;
t_init_b = realtime();
MPI_Init(&argc,
&argv);
t_init_e = realtime();
MPI_Comm_rank(MPI_COMM_WORLD,
&r);
MPI_Comm_size(MPI_COMM_WORLD,
&p);
if(r == 0)
t_calc =
MPI_Wtime();
MPI_Barrier(MPI_COMM_WORLD);
sum = 0.0;
h = (b - a) / n;
for(i = r; i < n; i +=
p)
sum += f(a + (i
+ 0.5) * h);
sum *= h;
if(r != 0)
MPI_Send(&sum,
1, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
if(r == 0)
{
double s;
for(i = 1; i
< p; i++)
{
MPI_Recv(&s,
1, MPI_DOUBLE, i, 0, MPI_COMM_WORLD, &st);
sum +=
s;
}
t_calc =
MPI_Wtime() - t_calc;
printf("%d\t,
%-15.3f\t, %-15.3f\t, %-15.3f\t;", p, difftime(t_init_e,
t_init_b)*1000,
t_calc*1000+difftime(t_init_e, t_init_b)*1000, t_calc*1000);
}
MPI_Finalize ();
return 0;
}
time_t realtime()
{
return time(NULL);
}
Для исследования
особенностей коммуникационной среды кластера МЭИ была разработана программа
ПМОВ, которая реализует передачу массива размером 2,56*106 элементов
типа double от первого вычислителя всем другим, участвующим в вычислении.
Программа МПОВ на языке C с использованием библиотеки
MPI представлена ниже.
#include <mpi.h>
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
int main(int argc, char* argv[])
{
int rank;
int size;
MPI_Init(&argc,
&argv);
MPI_Comm_rank(MPI_COMM_WORLD,&rank);
MPI_Comm_size(MPI_COMM_WORLD,&size);
if(rank == 0)
{
MPI_Status
status;
double* buf =
(double*)malloc(2560000*sizeof(double));
int ProcNam = 1;
int info;
double Time =
MPI_Wtime();
while(ProcNam
< size)
{
info =
MPI_Send(buf, 2560000, MPI_DOUBLE, ProcNam,
MPI_ANY_TAG, MPI_COMM_WORLD);
ProcNam++;
}
Time =
MPI_Wtime() - Time;
printf("Time
= %-15.3f\t\n", Time);
}
else
{
MPI_Status
status;
double* buf =
(double*)malloc(2560000*sizeof(double));
info =
MPI_Recv(buf, 2560000, MPI_DOUBLE, 0,
MPI_ANY_TAG, MPI_COMM_WORLD, &status);
}
MPI_Finalize ();
return 0;
}
3. Результаты
экспериментов
Эксперименты проводились на
кластере МЭИ в условиях общего доступа к вычислительным ресурсам. В каждом эксперименте
задавалось количество задействованных узлов и ядер на каждом из узлов.
Подсчитывалось полное время выполнения программы, и время выполнения программы
за вычетом времени на инициализацию MPI. Инициализация среды MPI –
это процесс подготовки к совместному использованию отдельных узлов кластера при
помощи библиотеки MPI, во время которого происходит создание MPI-структур
данных, нумерация вычислителей и другие подготовительные операции.
Для выявления зависимости
времени решения задачи численного интегрирования методом прямоугольников от
числа ядер с учетом инициализации среды MPI и без учета, была проведена
серия запусков теста 1 – программы МП.
В таблице 1 представлен
набор параметров запуска теста.
Таблица 1
Параметры запуска теста 1
|
Число узлов (1..16) |
Число ядер в узле (1..4) |
Общее количество ядер |
|
1 |
2 |
2 |
|
1 |
4 |
4 |
|
2 |
2 |
4 |
|
2 |
4 |
8 |
|
3 |
2 |
6 |
|
3 |
4 |
12 |
|
… |
… |
… |
|
16 |
2 |
32 |
|
16 |
4 |
64 |
При каждом запуске
регистрировалось время вычислений
программы МП с учетом инициализации и время вычислений без учета
инициализаций.
Графики зависимостей полного
времени работы программы МП (T, мкс) от количества ядер (N) и
времени работы без учета инициализации от количества ядер представлены на рис.
2 и 3.
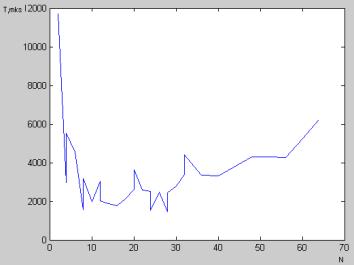
Рис. 2. График зависимости
полного времени работы от количества ядер
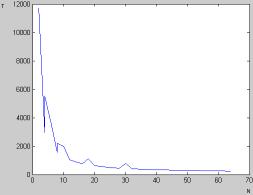
Рис. 3. График зависимости
времени работы без учета инициализации
от числа ядер
Для сравнения времени работы
при максимальном и минимальном удалении используемых ядер была проведена серия
запусков теста 2. Под удалением ядер следует понимать то, на каком уровне
передаются между ними данные, например, ядра одного процессора – минимальное
удаление, ядра разных узлов – максимальное удаление.
В таблице 2 представлены
параметры запуска теста 2.
Результаты проведения теста
2 графически представлены на рис. 4 и 5.
Таблица
2
Параметры теста 2, нечетные
строки – максимальное удаление,
четные – минимальное
удаление вычислителей в системе
|
Число узлов (1..16) |
Число ядер (1..4) |
Общее число ядер |
|
2 |
1 |
2 |
|
1 |
2 |
2 |
|
4 |
1 |
4 |
|
1 |
4 |
4 |
|
8 |
1 |
8 |
|
2 |
4 |
8 |
|
12 |
1 |
12 |
|
3 |
4 |
12 |
|
16 |
1 |
16 |
|
4 |
4 |
16 |
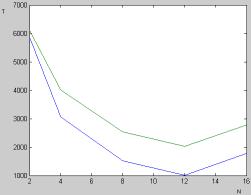
Рис. 4. График зависимости
полного времени работы от количества ядер, синим – минимальное удаление,
зеленым – максимальное удалением ядер в системе
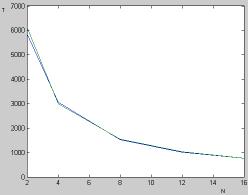
Рис. 5. График зависимости
времени работы без учета инициализации от количества ядер, синим – минимальное
удаление, зеленым – максимальное удалением ядер в системе
Для выявления зависимости
времени пересылки данных от расположения выбранных вычислителей в системе
проводим тест 3 - серию запусков программы ПМОВ с параметрами согласно таблице
2. Результат представлен на рис. 5.
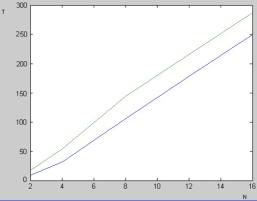
Рис. 5. График зависимости
времени работы от количества ядер,
синим – минимальное
удаление, зеленым – максимальное удаление ядер в системе
Анализ результатов
экспериментов, часть из которых представлена на рис. 2–5, показал следующее.
1. С увеличением числа ядер
уменьшается «чистое» время выполнения программы (без учета фазы инициализации MPI),
зависимость похожа на гиперболу.
При этом процессу
свойственно насыщение, когда увеличение числа ядер не дает сокращения времени
работы алгоритма.
2. Присутствуют отклонения
от общей закономерности, связанные с состоянием системы, коммуникационной
среды.
3. Зависимость «полного»
времени работы (с учетом фазы инициализации) также уменьшается с ростом N при
небольших значениях N. Начиная с некоторых значений числа ядер
наблюдается рост времени выполнения. Этот эффект можно объяснить тем, что время
на инициализацию среды перекрывает в этом случае выигрыш от использования
большего числа процессоров.
4. Время, затрачиваемое на
пересылку данных, существенно зависит от расположения используемых вычислителей
в системе.
Заключение
На основании проведенных экспериментов можно
говорить о значительном влиянии коммуникационной среды и системного
программного обеспечения на время решения задачи в кластерных системах. В
частности, возможны ситуации, когда общее время вычислений растет с ростом
числа ядер, участвующих в вычислительном процессе. Эти ситуации возникают тогда,
когда временные затраты на организацию параллельных вычислений превышают
выигрыш, связанный с распараллеливанием.
ЛИТЕРАТУРА
1.
Кластеры,
кластерные решения «Т-Платформы» [Электронный ресурс] : / «Т-Платформы». –
Электрон. дан. – М., 2003–2009. – Режим доступа:
http://www.t-platforms.ru/clusters , свободный.
2.
Богданов А.В.,
Станкова Е.Н. Архитектуры и топологии многопроцессорных вычислительных систем
[Электронный ресурс] / А.В. Богданов. – Электрон. текстовые дан. – М.:
INTUIT.ru: Интернет-Университет Информационных Технологий, 2003-2010. -.-Режим
доступа: http://www.intuit.ru/department/hardware/atmcs/4/ , свободный.
3.
Кластеры на
многоядерных процессорах: учебное пособие / И. И. Ладыгин,
А. В. Логинов, А. В. Филатов, С. Г. Яньков.- М.: Издательский дом
МЭИ, 2008. – 112 с.
4.
Лупин С. А.,
Посыпкин М. А Технологии параллельного программирования. –М.: Форум-Инфра-М,
2008. – 208 с.
5.
Топорков В.В.
Модели распределенных вычислений. – М.:Физматлит, 2004. – 320 с.
6.
Воеводин В.В.
Воеводин Вл.В. Параллельные вычисления – СПб.: БХВ – Петербург, 2002. – 608 с.
DEVELOPMENT AND USEGE OF TESTING
SOFTWARE FOR RESEARCH OF TASK SOLUTION FEATURES ON CLUSTER COMPUTING SYSTEM OF
THE MOSCOW POWER ENGINEERING INSTITUTE (TECHNICHAL UNIVERSITY)
Ivanov M. E.
Article is devoted to research of peculiar
properties of cluster computing systems, questions regarding requirement of optimization
of existent algorithms.
Keywords: parallel computing,
cluster, parallel algorithms.
Краткие сведения об авторе
Ф.И.О.: Иванов Максим Евгеньевич.
Место работы/учебы: филиал ГОУВПО «МЭИ(ТУ)» в г. Смоленске,
кафедра ВТ, магистратура, студент.
Г.р. 1987г.
Адрес: г. Смоленск, ул. Николаева д. 77
кв. 101.
Тел.: 40-65-50
Филиал ГОУВПО «МЭИ(ТУ)» в г. Смоленске
Smolensk Branch of the Moscow Power Engineering
Institute (Technical University)
Поступила в редакцию 28.09.2010.