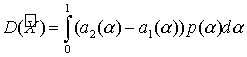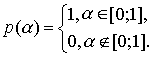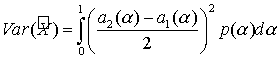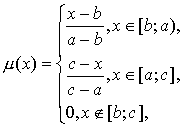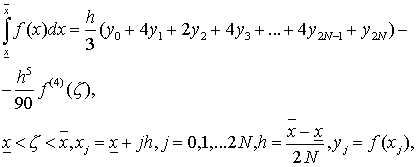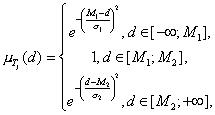Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 9. -

Вып. 4. - 2010. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-28-html/TITL-28.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-28-html/cont.htm

УДК 681.3

МЕТОДИКА КАЧЕСТВЕННО-КОЛИЧЕСТВЕННОГО ОЦЕНИВАНИЯ НАКОПЛЕНИЯ НЕЧЁТКОСТИ ПРИ ВЫПОЛНЕНИИ НЕЧЁТКИХ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ

Ó 20190 г. Зернов М. М., Стефанцов А. Г., Титов В. Л., Шаповалова Г. П.

(zernov.doc)

В работе предложена качественно-количественная методика оценивания реализаций расширенных нечётких арифметических операций по показателю накопление нечёткости. Методика основывается на выполнении реализованных операций над эталонными треугольными нечёткими числами и позволяет оценить степень накопления нечёткости по лингвистической шкале. Применяемые в качестве эталонов нечёткие треугольные числа, как правило, являются приемлемыми операндами для большинства существующих реализаций расширенных арифметических операций.

Ключевые слова: нечёткие вычисления, оценивание реализации нечётких операций.

Арифметические операции (сложение, вычитание, умножение, деление) являются базовыми элементами, на основе которых строятся разнообразные функции описания обстановки, результатов управляющих решений, функции аккумулирования влияний модельных сущностей. Помимо этого, арифметические операции над нечёткими числами могут быть применены и при построении операций сравнения нечётких чисел. Каждая из указанных операций может быть реализована различными способами, основанными на разном математическом аппарате.

Одним из основных показателей оценивания пригодности той или иной реализации расширенной арифметической операции является отсутствие или минимизация «накопления нечёткости» – роста меры размытости результата в ходе многократного использования расширенной операции. При наличии многократных, особенно итерационных, вычислений проблема размывания результата особенно важна. В ряде реализаций нечётких арифметических операций результат их многократного применения оказывается настолько размытым, что его носитель или даже множества достаточно высоких α-уровней покрывают весь базовый диапазон. Тогда результат оказывается сложно интерпретируемым и непригодным для дальнейшего анализа.

При этом полностью избежать размывания результатов для всех операций практически невозможно. Тем не менее, следует стремиться к уменьшению роста нечёткости результата.

С показателями качества реализации расширенной нечёткой операции, как правило, связаны критерии, позволяющие однозначно судить о пригодности реализации исходя из целей применения операции. При этом, несмотря на возможность получения количественной оценки значения показателя, в силу сложности интерпретации полученной количественной оценки, критерий пригодности зачастую формулируется качественно, например “требуется низкое накопление нечёткости” или “допустимо среднее накопление нечёткости”. В результате приходим к необходимости введения лингвистической шкалы над множеством значений показателя.

Заметим, что для ряда реализаций, возможно аналитическое определение накопления нечёткости без конкретизации операндов. В этом случае критерий, поддаётся самостоятельному анализу известными строгими методами на основе математической постановки реализации. Но, как правило, подобный анализ всё равно использует некоторые ограничения на вид анализируемых операндов, а также требует определённой методологической подготовки от лица, производящего оценивание. Более того, для некоторых реализаций, подобный анализ может оказаться намного сложнее собственно реализации операции и её экспериментальной проверки.

В результате, более эффективным с точки зрения трудозатрат является оценивание значения показателя по результату операции над эталонными операндами. Для проведения пробных операций над эталонами обычно достаточно математической постановки реализации.

Перейдём к непосредственному рассмотрению предлагаемой методики. Введём ряд обозначений.

Пусть – некоторая арифметическая операция, заданная на множестве действительных чисел (сложение, умножение, деление), тогда будет обозначать аналогичную ей операцию над нечёткими числами. В дальнейшем для простоты будем рассматривать двуместные случаи. Пусть даны два нечётких числа и , тогда результатом нечёткой арифметической операции будет некоторое нечёткое число , определённое на некотором базовом множестве действительных чисел.

Методика оценивания пригодности реализации расширенной нечёткой операции по показателю накопление нечёткости с критериальными требованиями, выраженными в количественно-качественном виде основывается на вычислительном эксперименте над числами стандартной треугольной формы и включает следующие этапы.

1. Выбираем меру нечёткости числа. Существует достаточно большое количество мер нечёткости (размытости) нечётких чисел. Для задачи определения возрастания нечёткости при применении той или иной реализации расширенной операции наиболее эффективно могут быть применены меры на основе отклонения функции принадлежности треугольного числа от модального значения [1]. В связи с этим предлагается два варианта меры.

1) Ширина нечёткого числа [2], определяемая как

,

(1)

где и – соответственно левая и правая границы множества α-уровня выпуклого нечёткого числа,

– весовая функция, удовлетворяющая условию нормировки.

В рамках рассматриваемой методики – тривиальная единичная функция:

,

2) Взвешенная дисперсия нечёткого числа [3]:

,

(2)

Принципиальной разницы между данными вариантами нет, поскольку в дальнейшем нас будет интересовать логарифм отношения меры результата к мере операндов, одинаковый для обеих мер при соответствующем выборе оснований (основание логарифма для отношения дисперсии равно квадрату основания для отношения ширины).

2. В качестве аргументов и задаются числа с треугольной формой функции принадлежности:

где – числовые параметры функции принадлежности – мода и границы возрастающей и убывающей линейных ветвей.

Для треугольных чисел, выражение (1) принимает вид:

.

(3)

А, выражение (2) в свою очередь преобразуется в:

(4)

Практика показывает, что указанная форма функции принадлежности операндов поддерживается любыми реализациями расширенных арифметических операций.

Зададим параметры функций принадлежности операндов так, чтобы эффективно протестировать реализации каждой из рассматриваемых арифметических операций, обеспечив попадание носителя результата для большинства операций в диапазон [1;5] и обеспечить равенство нечётких метрик (см. таблицу 1).

3. Вычисляем результат тестируемой реализации операции .

4. Вычисляем меру нечёткости результата или . Если результат выражается аналитически и также является треугольным числом, то применяем выражения (3) и (4).

Таблица 1 – Параметры операндов для тестирования реализации расширенной операции

Операция	Операнд	b	a	c
+,*,/		1	1,5	2	0,5	0,083
		1	1,5	2	0,5	0,083
-		1	1,5	2	0,5	0,083
		0	0,5	1	0,5	0,083

В противном случае следует воспользоваться способами приближённых вычислений интегралов, например по формуле Симпсона [4]:

(5)

где – число опорных точек ,

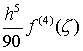– погрешность интегрирования.

5. Находим логарифм отношения метрик:

или

При, . В рассматриваемой методике применяются следующие основания:

6. Далее полученное значение следует оценить по лингвистической шкале , соответствующей рассматриваемой операции. Здесь – терм-множество лингвистической шкалы, – базовое множество лингвистической шкалы.

Каждый терм , описывается нечёткой переменной, в базовом множестве : .

Каждая из функций принадлежности имеет стандартный вид двусторонней гауссовой функции:

где и – соответственно нижняя и верхняя границы модального множества, а и – левый и правы коэффициенты нечёткости.

Определяем значения функций принадлежности по каждому терму шкалы в точке . В качестве оценки выбираем терм с максимальным значением функции принадлежности. В случае попадания в точку пересечения двух функций принадлежности, оценивать стоит по худшему варианту.

Шкала оценивания по операциям сложения и вычитания рассматривается на интервале [0;1.1] и представлена на рисунке 1. Параметры функций принадлежности термов шкалы представлены в таблице 2.

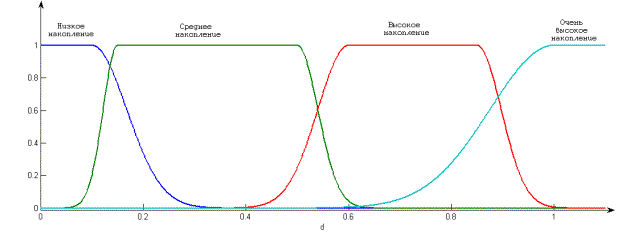
Рисунок 1 – Лингвистическая шкала оценивания накопления нечёткости для реализации операций сложения и вычитания

Шкала оценивания по операции умножения рассматривается на интервале [0.5;2] и представлена на рисунке 2. Параметры функций принадлежности термов шкалы представлены в таблице 3.

Шкала оценивания по операции деления рассматривается на интервале [-0.6;1], включающем и область отрицательных значений. Это связано с тем, что некоторые реализации операции деления приводят к уменьшению нечёткости результата по отношению к нечёткости операндов. Данная шкала представлена на рисунке 3. Параметры функций принадлежности термов шкалы представлены в таблице 4.

Таблица 2 – Параметры функций принадлежности термов шкалы оценивания операций сложения и вычитания

Терм
Низкое накопление	0	–	0,1	0,068
Среднее накопление	0,15	0,028	0,5	0,04
Высокое накопление	0,6	0,06	0,85	0,047
Очень высокое накопление	1	0,125	1,1	–

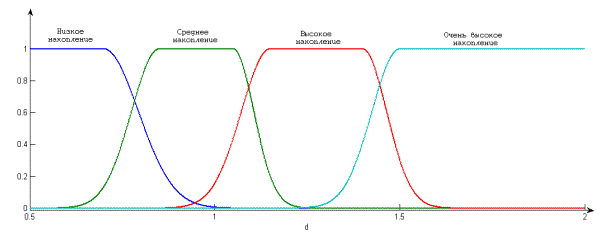
Рисунок 2 – Лингвистическая шкала оценивания накопления нечёткости для реализации операции умножения

Таблица 3 – Параметры функций принадлежности термов шкалы оценивания операции умножения

Терм
Низкое накопление	0,5	–	0,7	0,094
Среднее накопление	0,85	0,075	1,05	0,056
Высокое накопление	1,15	0,078	1,4	0,065
Очень высокое накопление	1,5	0,075	2	–

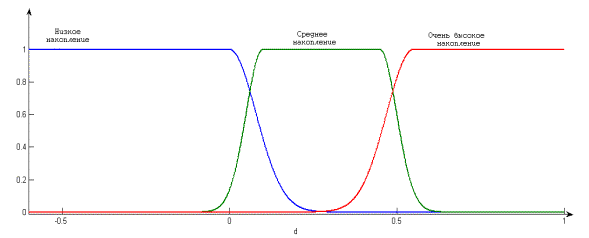
Рисунок 3 – Лингвистическая шкала оценивания накопления нечёткости для реализации операции деления

Таблица 4 – Параметры функций принадлежности термов шкалы оценивания операции умножения

Терм
Низкое накопление	-0,6	–	0	0,08
Среднее накопление	0,1	0,05	0,45	0,05
Очень высокое накопление	0,55	0,08	1	–

Если отбросить последний этап методики, то получаем в чистом виде количественную оценку показателя. Однако введённые экспертами шкалы позволяют дать качественную интерпретацию рассчитанного значения с точки зрения диапазона, в котором варьируется данная оценка на практике.

литература

1. Федулов А. С. Вид взаимодействия нечётких чисел, ограничивающий возрастание неопределенности при выполнении операций нечёткой арифметики // Вестник МЭИ.– 2006.– № 1.– C. 101– 110.

2. Насибов Э.Н. Некоторые интегральные показатели нечетких чисел и визуально-интерактивный метод определения стратегии их вычисления// Известия РАН. Теория и системы управления, 2002, № 4, с. 82-88.

3. Fuller R., Majlender P. On interactive fuzzy numbers// Fuzzy Sets and Systems, 2004, vol. 143, pp. 355–369.

4. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – 13-е изд., исправленное. – М.: Наука, Гл. ред. физ.-мат. Лит., 1986. – 544 с.

PROCEDURE OF QUANTITATIVE-QUALITATIVE ESTIMATING OF FUZZINESS ACCUMULATION FOR EXTENDED FUZZY ARITHMETICAL OPERATIONS IMPLEMENTATION

Zernov M. M., Stefantsov A.G., Titov V.L., Shapovalova G.P.

Procedure of quantitative-qualitative estimating of extended fuzzy arithmetical operation realizations by index of fuzz in essaccumulation is of fered in this article. The procedur ebases on realized operations implementation to etalon triangular fuzzy numbers and allows estimating fuzz in essaccumulation degree by linguistic scale. Triangular fuzzy numbers, used as etalons, are usually adoptable operands for most of existing of extended fuzzy arithmetical operation realizations.

Key words: fuzzy evaluating, estimating of fuzzy operation realizations.

Зернов Михаил Михайлович, к.т.н.

Стефанцов Алексей Геннадьевич, к.т.н.

Титов Владимир Леонтьевич, к.т.н.

Шаповалова Галина Павловна, к.т.н., доцент

zmmioml@yandex.ru

Филиал ГОУ ВПО «МЭИ (ТУ)» в г. Смоленске

Поступила в редакцию 21.12.2010.