Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 10. -

Вып. 1. - 2011. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-29-html/TITL-29.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-29-html/cont.htm

 

УДК 532.5.516(04)

 

НЕСТАЦИОНАРНАЯ ЗАДАЧА НАВЬЕ-СТОКСА ДЛЯ НЕСЖИМАЕМОЙ ЖИДКОСТИ С ВЯЗКОСТЬЮ

 

Ó 2011 г. Омуров Т. Д.

 

(omurov.doc)

 

Доказательство существования и гладкости решений уравнений Навье-Стокса является шестой задачей тысячелетия. Задача сформулирована Математическим институтом Клэя в 2000 году. Уравнения описывают движение вязкой несжимаемой жидкости в гидродинамике, например, поток крови. В работе дано доказательство существования и гладкости решений уравнений Навье-Стокса в формулировке задачи, предложенной институтом Клэя.

Ключевые слова: течение, жидкость, вязкость, Навье-Стокс, проблема, тысячелетие,  решение.                                             

 

Введение

Целью работы является доказательство существования и гладкости решений нестационарной задачи, описываемой уравнениями Навье-Стокса [1].

         В данной работе разработан метод решения поставленной институтом Клэя задачи, названный методом эквивалентного раздробления и впервые описанный в работе [2]. В первом параграфе изучаются уравнения идеальной жидкости, т.е. без трения [3]. Для идеальной жидкости имеет место строгое решение, которое получено на основе метода эквивалентного раздробления [2]. В параграфе 2 метод эквивалентного раздробления системы применен для течений с трением, т.е. для уравнений Навье-Стокса.

         Не нарушая полный смысл задачи Математического института Клэя [1], дадим постановку задачи в следующем виде.

         Пусть  – трёхмерный вектор скорости жидкости, x=(x, y, z),  P(x, t) –  давление. Уравнения Навье-Стокса в векторной форме имеют вид

                                                           (1)

с условием

,                                                                  (2)

где >0 – кинематическая вязкость, – плотность,  – внешняя сила, Ñ – оператор набла и D – оператор Лапласа, т.е. лапласиан Ñ×Ñ. Векторное уравнение (1) содержит три скалярных уравнения. Обозначая компоненты векторов скорости и внешней силы

        

  

,

получаем соответствующие скалярные уравнения Навье-Стокса

         .

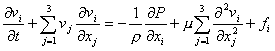Неизвестными величинами являются скорость v и давление P, т.е. четыре неизвестных: три компоненты скорости и давление, поэтому необходимо еще одно уравнение. Дополнительным уравнением является условие несжимаемости жидкости

                                                 .                                                             (3)

 

§ 1. Течения без трения

 

Теория идеальной жидкости неприменима, если учитывается сопротивление тела, движущегося в реальной жидкости [3]. Например, для несжимаемых течений без трения получаются строгие решения. В этом случае уравнения Навье-Стокса упрощаются, так как    поэтому система (1) приводится к виду

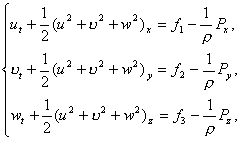
                                                                      (1.1)

при выполнении условия  Стокса

 .

Поэтому сформулируем следующую теорему.

Теорема 1.1. При условиях (2), (3) и выполнении условия Стокса, когда ,  система  (1.1) преобразуется к эквивалентному виду

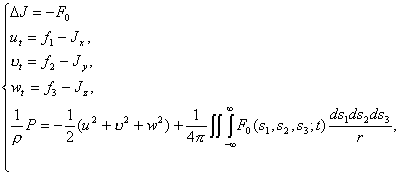                                               (1.2)

где

     

      

   .

Следовательно, система (1.2) однозначно разрешима в C2,2,2,1(T).

         Доказательство. В системе (1.1) первое уравнение системы (1.1) дифференцируем по x, второе – по y, третье – по z, а затем суммируем. Получаем уравнение Пуассона [4]

          .                                                                                                                   (1.3)

В работе Соболева С.Л. [4] указано, что функция

                                                                     (1.4)

удовлетворяет уравнению (1.3) и называется ньютоновым потенциалом. При этом имеет место:

а) стремление к нулю функции J на бесконечности;

б) существование непрерывных первых производных у ньютонового потенциала.

Введем новые переменные:   , чтобы доказать существование и непрерывность вторых производных. Из интеграла

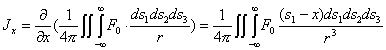                                         (1.5)

получим

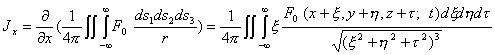           .           (1.6)

Аналогично, имеем

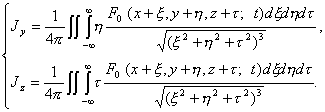                                              (1.7)

Интегралы (1.6), (1.7) допускают дифференцирование по x, y, z, причем интегралы от производных сходятся равномерно.

Теперь, остается доказать, что ньютоновый потенциал удовлетворяет уравнению Пуассона. Для этого возьмем функцию , равную нулю всюду, кроме некоторого шара C с центром в точке (x, y, z), и имеющую непрерывные производные нескольких порядков [4]. Так как вне шара C функции  и  равны нулю, то по формуле Грина получим:

                                                       (1.8)      

Умножая  выражения (1.8) на F0 (x, y, z; t) и интегрируя по x, y, z, имеем

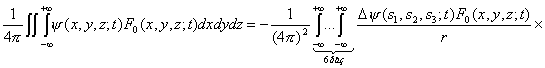
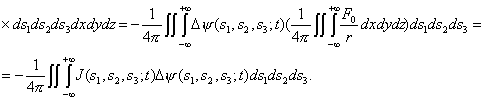                      (1.9)

Последний интеграл преобразуется с учетом того, что в достаточно большой области D

                                       (1.10)

Сопоставляя (1.10) с (1.9), приходим к заключению, что

         .                                                      (1.11)

Из произвольности  в (1.11) вытекает

что и требовалось доказать. Значит, уравнение (1.3) есть первое уравнение системы (1.2).  

Теперь, если  J(x, y, z, t) – решение уравнения (1.3), то подставляя

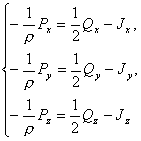                                                                                            (1.12)

в систему (1.1), получим

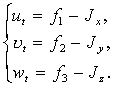                                                                                                                (1.13)

Система (1.13) является вторым, третьим и четвертым уравнениями системы (1.2), поэтому решение   ищем в виде:

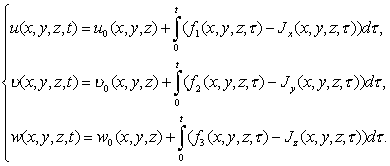                                           (1.14)

Следовательно, учитывая  из функции (1.4) имеем

,                                                    (1.15)

а это есть пятое уравнение системы (1.2), что и требовалось доказать. 

Лемма 1.1. При условиях теоремы 1.1 система (1.1) разрешима в (u, v, w)Î C2,2,2,1(T).

В общем случае, по рассмотренной схеме невозможно решить систему уравнений Навье-Стокса, так как не выполняется условие Стокса для течений с трением. Следовательно, необходимо модифицировать метод, из которого следовало бы гладкое решение уравнений Навье-Стокса в классе:

– гладкости функций (u, , w) требуются только по x, y, z, так как производную первого порядка во времени определяем для t>0 при заданных для t=0 начальных условиях: ()|t=0 =().  

 

§ 2. Течения с трением                                                           

 

Задача Навье-Стокса рассматривается для несжимаемой жидкости и известны частные решения для ламинарного течения в трубе или для течений в пограничном слое [3]. Частные решения проверены экспериментом, что гарантирует общую применимость уравнений Навье-Стокса для исследования течений. Доказательство существования гладких решений уравнения Навье-Стокса по (x, y, z) дает метод решения задачи для уравнений Навье-Стокса.

Рассмотрим задачу Навье-Стокса

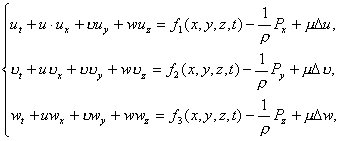                                                     (2.1)

                              (2.2)

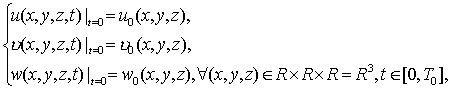                              (2.3)

где уравнение (2.2) есть уравнение неразрывности. Неизвестными величинами являются скорость v: (u, v, w) – три компоненты скорости и давление P, причем . Возникает вопрос о разрешимости задачи для уравнений Навье-Стокса и гладкости всех его решений по x,y,z.

Решение задачи для уравнений Навье-Стокса методом эквивалентного раздробления дает ответ на поставленный вопрос.

Систему (2.1) приводим к виду

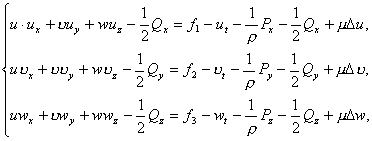                                             (2.4)

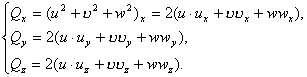                                                          (2.5)

Из системы (2.4) видно, что в систему (2.1) справа и слева введены функции

 так, что не нарушена эквивалентность систем (2.1) и (2.4). На основе функций  систему (2.4) преобразуем к виду:

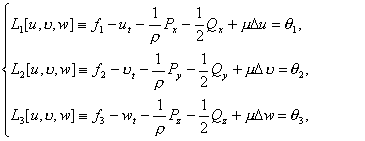                                              (2.6)

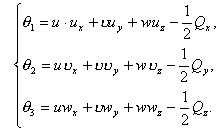                                                                          (2.7)

 назовем «исправленными» дифференциальными операторами типа теплопроводности. Полученные системы (2.6) и (2.7) содержат неизвестные:  и давление, причем системы (2.4), (2.6) и (2.7) эквивалентны.

Рассмотрим, каким образом порождается уравнение относительно давления при условии (2.2).  Для этого в настоящей работе, впервые, предложены три схемы решения систем (2.6) и (2.7).

         Схема 1. Пусть функции  допускают условие Стокса:

                                                                                 (2.8)      

          .                                                                                         (2.9)

Причем это не означает, что условие (2.8) выполняется относительно:  так как в исходная задача для уравнений Навье-Стокса содержит трение [3]. Рассмотрим, когда (2.8) не выполняется. Покажем, что случай  допускает только условие (2.8).

Отметим, что выбор схемы зависит от того, выполнены ли условия (2.8)-(2.9) относительно функций . Но это известные функции и определяются в виде

           

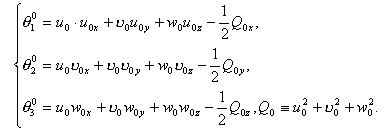
Например, как необходимые условия введения схемы 1, должны выполняться

      

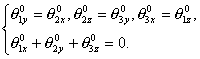
Утверждение 2.1. Если выполняются условия (2.2), (2.3), (2.8), (2.9),то системы (2.6), (2.7) эквивалентно преобразуются к виду

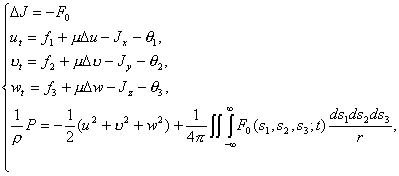                                             (2.10)

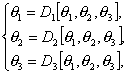                                                                                                               (2.11)

соответственно, где     ,

                                                                                                                                       поэтому система (2.10) разрешима  в .

 

Доказательство. Дифференцируя в системе (2.6) первое уравнение по x, второе – по y, третье – по z, а, затем, суммируя их с учетом (2.2) и (2.9), получим уравнение Пуассона [4]

            ,                                                                                              (2.12)

при этом (см.(1.4)): , , причем

                                                     (2.13)

Тогда из системы (2.6) имеем

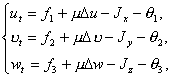                                                                                     (2.14)

см. (1.7):   .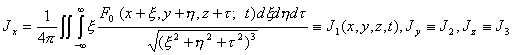

Уравнения (2.12), (2.14) это есть первое, второе, третье и четвертое уравнения системы (2.10).

Система (2.14) решается методом  Соболева С.Л. [4]:

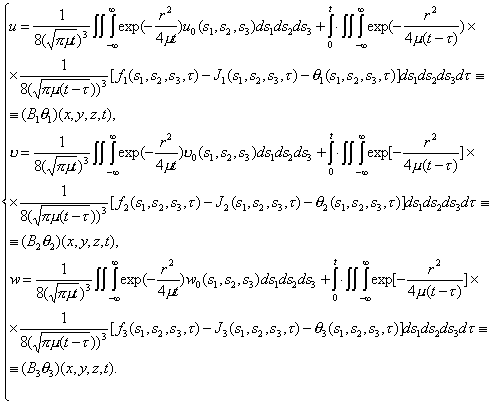              (2.15)

Далее, учитывая (2.7) и (2.15), получим

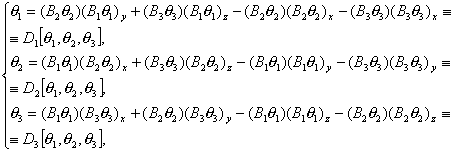                            (2.16)

см. систему (2.11).

В самом деле, на основе (2.7) и (2.15) и их в частных производных

 

 

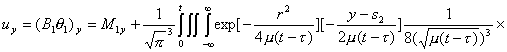
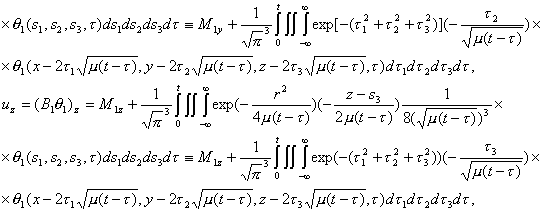
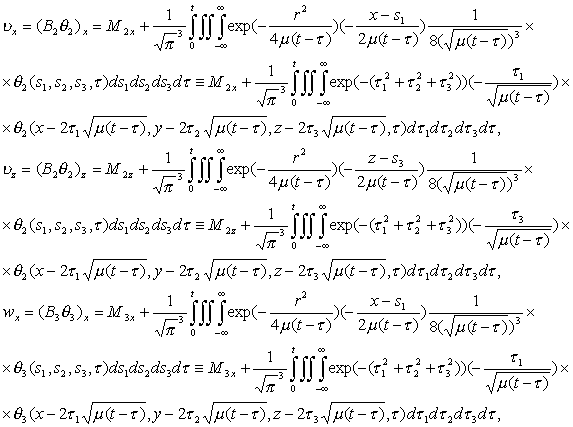
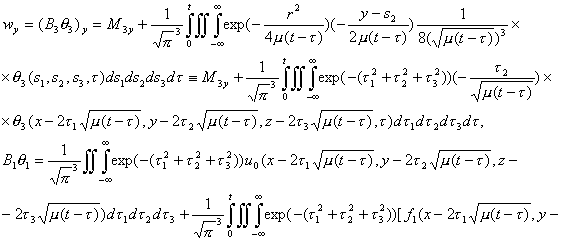
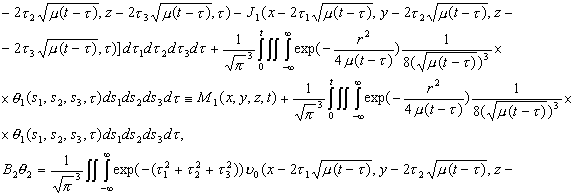
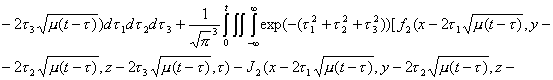
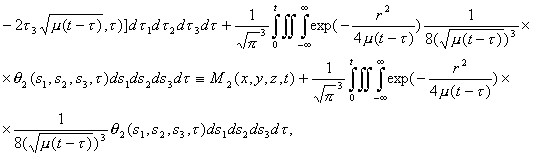
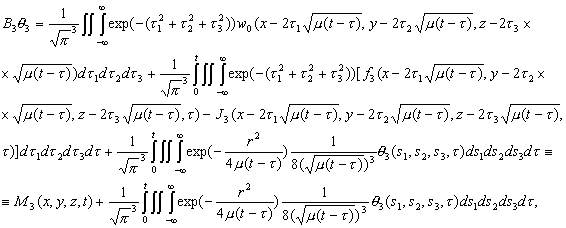
получаем систему (2.16). Поскольку система (2.16) – это система нелинейных интегральных уравнений Вольтерра 2-го рода по переменной t (состоит из трех уравнений), то она имеет единственное решение  

Предложение 2.1. При выполнении (2.8), (2.9) решение системы (2.16):  удовлетворяет уравнению Лапласа [4]  , , а потому являются гармоническими функциями.

Из полученных результатов схемы 1 следует, что функции

, определяются из системы (2.15) и (2.16). Следовательно, на основе

                                                        (2.17)   

получим

        .                               (2.18)

Отсюда видно, что  и уравнение (2.18) есть уравнение типа Бернулли, и это пятое уравнение системы (2.10). Что и требовалось доказать. 

Замечание 1.  Согласно результатам схемы 1 функции

определяются из системы (2.15). Поэтому, учитывая (2.2), (2.9) и суммируя

                                                                                 

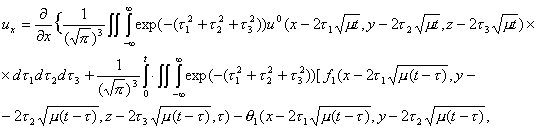
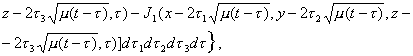
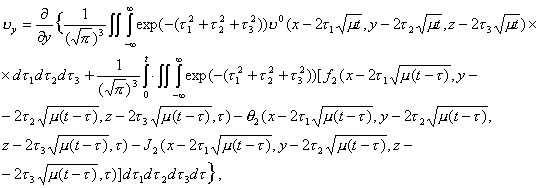
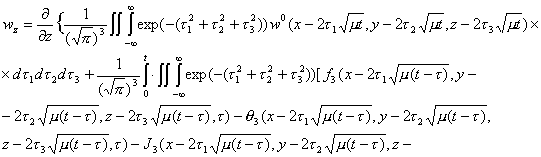
получим

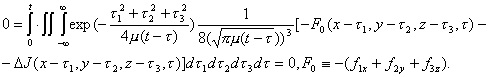
Таким образом, система (2.15) удовлетворяет уравнению (2.2).

Теорема 2.1. При условиях (2.2), (2.3), (2.8) и (2.9) нестационарная задача Навье-Стокса (2.1)-(2.3) разрешима в

Схема 2. Пусть функции  допускают только условие (2.9): . Тогда из системы (2.6) и (2.7), учитывая схему 1, имеем системы (2.10), (2.11), поэтому решение представляется в виде

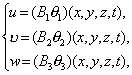                                                                                               (2.19)

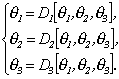                                                                                                                  (2.20)

Здесь функции  определяются из системы (2.20) с соответствующим дифференцированием по x, y, z.

            Лемма 2.1. Система интегральных уравнений Вольтерра 2-го рода по переменной t (2.20) имеет единственное решение  в . Поэтому решение данной системы можно найти методом Пикара

                                                       (2.21)

где  – начальные приближения.

Лемма 2.2. При условиях леммы 2.1 система (2.19) разрешима в .

            На основе вышеуказанных лемм и  (2.17), находим давление

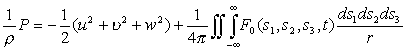            .                 (2.22)

Теорема 2.2. Если выполняются условия (2.2), (2.3), (2.9) леммы 2.2 и условие (2.22), то задача (2.1)-(2.3) имеет не более одного решения в D0(T).

Замечание 2. Когда выполняются условия схемы 2, решение системы (2.20) не удовлетворяет условию предложения 2.1, т.е.  не являются гармоническими функциями, в чем и заключается отличие схемы 2 от схемы 1.   

Схема 3. Пусть функции  удовлетворяют условию (2.8). Тогда можно требовать, чтобы

,                                                                           (2.23)

где  – новая неизвестная функция. Поэтому из системы (2.6) и (2.7), получим следующие системы

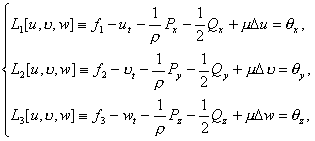                                                       (2.24)

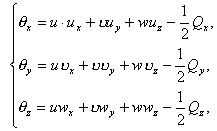                                                                             (2.25)

соответственно.

Утверждение 2.2. При условиях (2.2), (2.3), (2.8) и (2.23), системы (2.24) и (2.25) эквивалентно преобразуются к виду

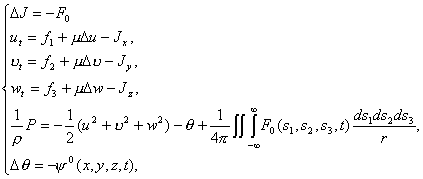                        (2.26)

где    

            

поэтому система (2.26) разрешима  в .

Доказательство. Первое уравнение (2.24) дифференцируем  по x, второе – по y, третье – по z и, затем, суммируя с учетом (2.2), получим

  .                                                                                               (2.27) 

Решение данного уравнения представляется в виде

             .                                    (2.28)

 Следовательно, на основе

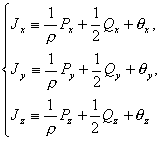                                                                                                       (2.29)

из системы (2.24) получим

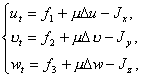                                                                                                          (2.30)

             

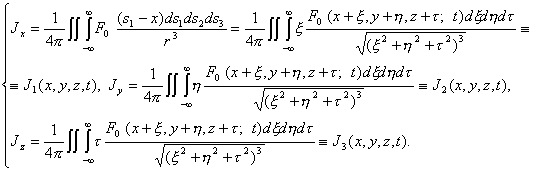
Уравнения (2.28) и системы (2.30) это есть первое, второе, третье и четвертое уравнения системы (2.26). Решая систему (2.30) методом  Соболева, имеем

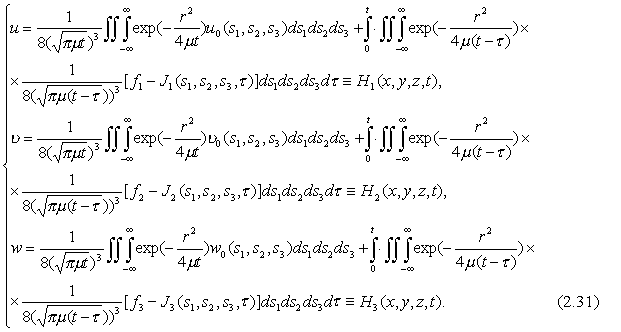
 являются известными функциями  и

определяются из системы (2.31) следующим образом:   

       ;

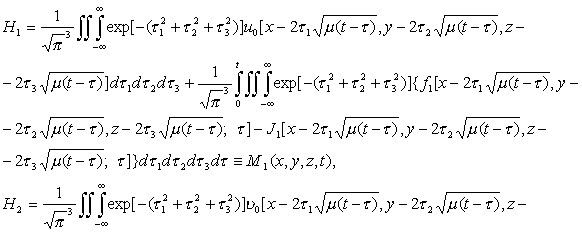
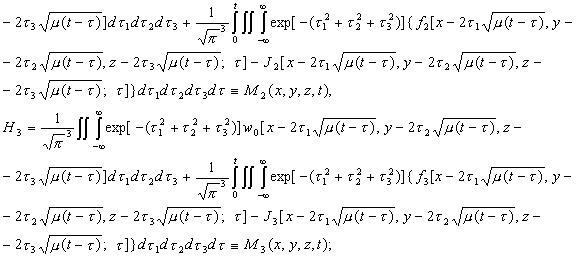
 Поэтому на основе выражений (2.25), (2.31) и их в частных производных по x, y, z, находим

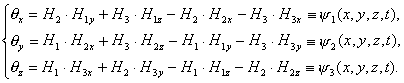                                     (2.32)

Так как правая сторона системы (2.32) определяется функциями , то  становятся известными функциями.

Для определения  систему (2.32) дифференцируем по x, по y, по z и, суммируя, имеем уравнение Пуассона [4]

           ,                                                                                                (2.33)

которое однозначно разрешимо в :

. 

Уравнение (2.33) – это шестое уравнение системы (2.26). Следовательно, учитывая выражение (2.28), получим

         ,      .                     (2.34)

Замечание 3. Из результатов схемы 3 следует, что функции:  определяются из системы (2.31). Тогда учитывая (2.2) и суммируя

  

                                                                                     

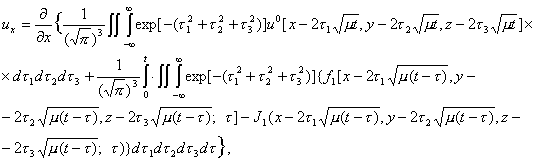
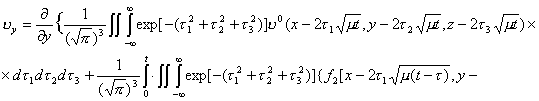
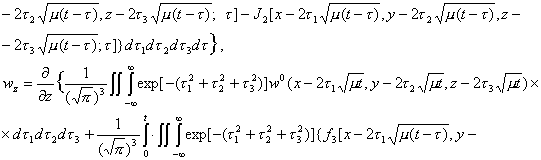
имеем

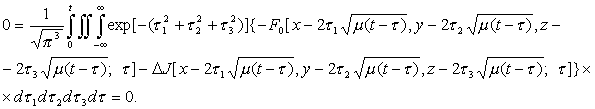
Значит, система (2.31) удовлетворяет уравнению (2.2), что и требовалось доказать.

Теорема 2.3. Если выполняются условия (2.2), (2.3) и (2.23), то задача (2.1)-(2.3) разрешима в    

         Критерий гладкости решений задачи для уравнений Навье-Стокса. Задача (2.1)-(2.3) имеет гладкое единственное решение в , т.е. по (x, y, z),  тогда и только тогда, когда «исправленные» операторы типа теплопроводности допускают условия или схемы 1, или схемы 2, или схемы 3, где функции  определяются в виде «исправленных» операторов.

                                              

                                                      Примечание

          а) метод эквивалентного раздробления системы можно применить к задачам Навье–Стокса в ограниченной области;

б) на основе метода эквивалентного раздробления системы можно решать стационарную задачу Навье-Стокса;

в) результаты работы обобщаются на задачи Навье-Стокса, когда uÎRn, xÎRn, tÎ[0, T0].

 

Литература

 

1. Существование и гладкость решений уравнений Навье-Стокса //Задачи тысячелетия, сформулированные в 2000 году Математическим институтом Клея.

2. Омуров Т.Д. Нестационарная задача Навье-Стокса для несжимаемой жидкости. – Бишкек: Изд-во КНУ им. Ж. Баласагына, 2010. – 21 с. (Регистр Кыргызпатента: авторское свидетельство №1543 от 30.07.2010 г.).  www.university.kg

3. Шлихтинг Г. Теория пограничного слоя. – М.: Наука, 1974. – 712 с.

4. Соболев С.Л. Уравнения математической физики. – М.: Наука, 1966.– 443 с.

 

Nonstationary problem Navier-Stokes for incompressible fluid

 

Omurov T. D.

 

Existence and smooth solution of the Navier-Stokes equation is one of the most important problems in mathematics of the century stated by Clay Mathematics Institute in 2000, which describes the motion of viscous Newtonian fluid, for example, flow of blood, and which is a basic of hydrodynamic. The chief object of this work is to prove existence and smooth solution of nonstationary problem Navier-Stokes for incompressible fluid.

Key words: flow, fluid, viscosity, Navier-Stokes, problem, millenium, solution.

                                                      

 

Омуров Т.Д. – д.ф.-м.н., проф., заведующий кафедрой дифференциальных уравнений Кыргызского Национального университета имени Ж. Баласагына.    E-mail: omurovtd@mail.ru

 

Кафедра дифференциальных уравнений

Кыргызский Национальный университет имени Ж. Баласагына

Поступила в редакцию 17.03.2011.