Оптимизация условий культивирования, влияющих
на синтез микроорганизмами экономически
значимого продукта
Ó 2011 г. Шулюпин О.К.
Аннотация
Рассмотрены
ограничения двухуровневого полного факторного эксперимента при решении задач
нахождения оптимальных условий культивирования
как некорректно поставленной задачи и предложен путь регуляризации через
оценки значимости коэффициентов полинома с применением непараметрических критериев, построения графиков, корреляционных
таблиц и корреляционных полей до
решения системы линейных уравнений.
Предисловие
Развитие биотехнологии, совершенствование рационов
вскармливания сельскохозяйственных животных и растений, расширение производства
пищевых добавок для людей ставят задачу быстрого поиска компонентов питания с
повышенной биологической активностью. В опубликованной литературе задачи
оптимизации рационов разработаны достаточно глубоко, но задачи оптимального
поиска компонентов питания с повышенной биологической активностью разработаны
слабее и на наш взгляд не отвечают современным потребностям промышленности и
сельского хозяйства.
Микроорганизмы являются наиболее простыми из
самостоятельно живущих организмов и, возможно, наиболее значимыми элементами в
процессах биотехнологии, то основные примеры приведены из области микробиологии. По нашему мнению,
предлагаемые математические и методологические подходы могут быть легко
обобщены и для более сложных продуцентов, поскольку регуляция активности
оперона условиями внешней среды одинакова для всех известных организмов [15].
Из всех биологических наук микробиология – наиболее точная и наиболее математизированная. Ряд задач микробиологии невозможно решить без математической обработки результатов измерений, по крайней мере, некоторых свойств и параметров микробиологической популяции и без применения хотя бы простейших математических моделей. Важность такого подхода подтверждается тем, что микроорганизмы являются продуцентами многих уникальных физиологически активных соединений, к которым можно отнести ферменты, антигены, антибиотики как наиболее значимые.
Современные технологические процессы невозможно вести без применения математики. Рост фармацевтической промышленности и биотехнологии в последнее время вызывает увеличение спроса на промышленно важные микроорганизмы.
Многие микроорганизмы
способны синтезировать ряд ЦП, которые не синтезируют другие организмы.
Но нередко перспективный штамм производит синтез экономически важного целевого
продукта при выращивании на плотной питательной среде и не способен
синтезировать его при глубинном культивировании. Возможен вариант, когда
глубинное культивирование на питательных средах с использованием гидролизатов и
вытяжек из сырья природного происхождения
не обеспечивает стабильного получения ЦП и выход ЦП сильно зависит от
партии питательной среды. Это ухудшает технологические показатели продуцента и
может служить основанием для отказа от такого микроба при использовании в
промышленных масштабах. В таком случае можно говорить о наличии
метаболизируемых ингибиторов или индукторов нужного синтеза. Молекулярное
клонирование и прочие генно - инженерные операции не решают проблемы, поскольку
в изученный продуцент переносят рекомбинантную ДНК вместе с регуляторными
участками. Необходимо проводить комплексное изучение продуцента.
Встает
вопрос о возможности нахождения
регуляторных факторов и переходе к управляемому культивированию.
Названную операцию можно осуществить, если производить целенаправленный активный поиск регуляторных факторов.
Процесс
поиска осложняется тем, что в качестве регуляторного фактора могут выступать
несколько индивидуальных химических соединений разных классов (минеральные
компоненты, углеводы, источники азота и т.д.), либо иных условий
культивирования (рН, аэрация…) действующих одновременно и взаимовлияюще.
Применение
микроорганизмов в технологическом процессе предъявляет ряд требований к
свойствам промышленного штамма – глубинное культивирование, рентабельный выход
ЦП, безопасность для окружающей среды, наличие
нескольких селективных маркеров, желателен выход ЦП в культуральую
среду, низкий уровень спонтанного мутагенеза и т.д..
Знание
общих закономерностей питания микроорганизмов мало что дает при работе с
конкретным продуцентом. Необходима стратегия поиска лимитирующих, ингибирующих
и индуцирующих нужный синтез факторов (регуляторных факторов) среди множества
возможных кандидатов из многочисленных потенциально осуществимых условий
культивирования.
Выяснение
количества и роли регуляторных факторов позволяет решить вопрос о
целесообразности применения мутагенеза и перехода от дикого штамма к более
технологичному мутанту.
Задача
поиска регуляторных факторов осложняется наличием значительного межфакторного
взаимодействия (сильная кривизна поверхности отклика - зависимости ВП от
условий культивирования). При таких начальных условиях серия однофакторных
экспериментов дает мало информации, а в ряде случаев, при наличии нескольких
регуляторных факторов, в принципе не позволяет решить задачу поиска. Необходимо
проводить многофакторный поиск, используя индивидуальные химические соединения
в серии многофакторных экспериментов по планам, близким к оптимальным для
поиска.
Последовательность
применения математики в микробиологической работе – количественное
измерение одного или нескольких
свойств, построение таблиц, построение графиков, разработка регрессионных
зависимостей, построение математических моделей. Для проведения поиска
регуляторных факторов, близкого к оптимальному, нередко достаточно даже качественных измерений с неизвестной
ошибкой, построения на этих основаниях таблиц и графиков, что не требует ни
большого количества арифметических вычислений, ни повышенной математической
подготовки.
Успехи,
достигнутые при изучении и оптимизации процессов, зависящих от большого
количеств факторов, стали возможными благодаря широкому внедрению
математических методов планирования эксперимента. Возникает необходимость
изменения методологии биологических исследований. Принцип поочередного
изменения в эксперименте каждого фактора на фоне постоянного уровня остальных
(метод Зайделя – Гаусса /1/) не является универсальным и окончательным, а всего
лишь часть комплексного исследования объекта, нередко применимого только на
ранних стадиях исследования. Биологические системы, зависящие от большого
количества факторов с сильным межфакторным взаимодействием при современных
требованиях практики сложно изучать, моделировать и управлять процессами на основе
мало связанных однофакторных зависимостей. Методология проведения и трактовки
однофакторных зависимостей хорошо разработана и в дополнительных объяснениях,
на наш взгляд, не нуждается /1/.
Представление
полученных нередко весьма разнородных
результатов измерений в виде графиков, таблиц, корреляционных полей, нахождение
аналогий с более изученными родственными объектами служат основой к проведению
активных поисковых работ и дальнейшей оптимизации процесса с количественным
учетом влияния нескольких факторов на синтез ЦП.
Состояние популяции микробов существенно зависит от
разнообразных по своему характеру (качественно различных) и по интенсивности
(количественно различных) факторов. Поэтому пред современным микробиологом
стоит задача – комплексное исследование объекта, установление
причинно-следственных связей между различными явлениями, выделение управляемых
факторов и воздействие на них.
Молекулярное клонирование не решает проблемы, т.к. в
состав гибридного репликона переносят структурный ген вместе с регуляторными
участками. После решения задачи поиска регуляторных факторов возможна
дальнейшая генетическая модификация исходного продуцента, либо замена природных
регуляторных факторов на их более удобные с точки зрения технолога синтетические
аналоги, если таковые можно получить.
Активные поисковые работы с учетом ожидаемой зависимости
изучаемого параметра от нескольких факторов лучше начинать с отсеивающего
эксперимента.
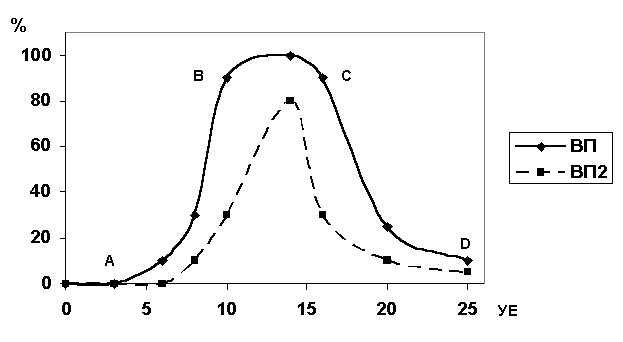
Рисунок 1. Зависимость
выхода процесса от концентрации метаболизируемого индуктора в питательной
среде.
В простейшем
случае, когда ВП зависит от одного фактора, можно отобразить зависимость в виде двумерной кривой, рис.1.
Можно выделить следующие участки 0 – А допороговый уровень концентрации
регуляторного фактора, нераспознаваемый микроорганизмом, не вызывающий нужного
синтеза, А – В участок лимитирования, В – С
уровень насыщения влияния регуляторного фактора, С – D участок ингибирования нужного синтеза контролируемым фактором (группой факторов).
На рис.1 отображен наиболее общий случай. Углы наклона кривой (первая
производная) в каждой точке будут строго индивидуальны и могут варьировать в
широких пределах. В частности, некоторые факторы могут не достигать уровня
ингибирования, прерываясь на т.С., например аэрация для аэробов, интенсивность
перемешивания и т.д.
При влиянии
на ВП второго фактора кривая может
сильно изменится (кривые 1 и 2, рис.1). Горизонтальные участки на зависимости
ВП от интенсивности фактора говорят о переключении внутренних механизмов,
возможно о включении новых оперонов - диауксия.
Для каждого
конкретного продуцента и конкретного ВП необходимо определить количественно эти
концентрации (интенсивности) и выделить их как управляемые переменные, за
которыми необходим первостепенный контроль; найти общий фон прочих питательных
веществ и условий культивирования, обеспечивающих возможность нужного синтеза,
как достаточно постоянных параметров технологического процесса. Наибольшую
важность для технолога представляет знание ширины участка насыщения и границы
переходов на уровни лимитирования и ингибирования регуляторным фактором
(технологический оптимум). Необходимо не только найти условия максимального
выхода ЦП, но и описать пограничные условия снижения ВП и, по возможности,
знать хотя бы некоторые условия, влияющие на снижение уровня ЦП от желаемого
уровня.
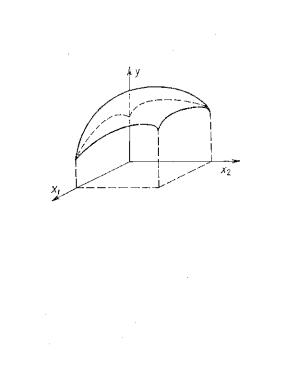
Рисунок 2. Один из возможных
видов участка поверхности отклика в окрестности максимума (случай двух
переменных). Цит. по [18].
В пространстве участок поверхности отклика вблизи
максимума будет представлен фрагментом параболоида или двухполостного гиперболоида.
Максимальное значение функция отклика будет достигать в некой точке. С учетом
неизбежной в практической работе ошибки измерения ВП и неустранимой ошибки в
задании управляемых переменных – некая
ограниченная область. С точки зрения технолога – наиболее удобный для
практической работы вариант, поскольку небольшие изменения управляемых
переменных не приведут к значительному изменению ВП, процесс будет достаточно
устойчив к небольшим возмущениям.
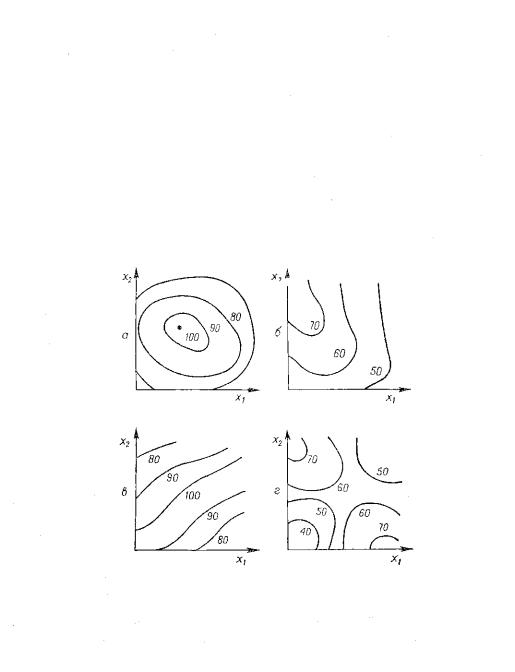
Рис 3. Возможные проекции
сечений поверхности отклика. Линии равного выхода. Случай двух переменных. Цит.
по [18].
На рис.3 а – поверхность отклика типа рис.2
(шапочка), работу можно считать завершенной, технологический оптимум
найден. Вариант 3 б – стационарное
возвышение. В этом случае максимальное значение сосредоточено вдоль некой линии
и достаточно протяженно. В пространстве на небольшом интервале – параболический
или гиперболический цилиндр. Случай 3 в – близкий к случаю 3 б, просто меньшая
кривизна поверхности отклика на достаточно большом участке. Эти варианты –
возможный переходный этап к последующей работе – прохождению вдоль хребта.
Идеальный случай – если удастся найти неострую вершину типа 3 а. Неплохой
вариант – найти плато на хребте. В крайнем случае – найти такой участок хребта,
где максимально пологие склоны. Такой вариант тоже обеспечит устойчивость
технологического процесса.
Случай 3 г – седло, в одном направлении функция
отклика возрастает, в другом убывает. Самый неудобный для технолога случай –
неустойчивый оптимум. Дальнейшая работа по поиску оптимальной области
затруднительна и проблематична, хотя и не удобна для технолога. Достаточно
интересный и перспективный случай для исследователя. Нельзя исключить варианта,
что удастся найти некие дополнительные условия культивирования, которые
принципиально повлияют на метаболизм продуцента и поверхность отклика
радикально изменится, перейдет в поверхности типа 3 а или 3 б. В пространстве –
гиперболический параболоид, седловидная поверхность.
Рассмотрены простейшие случаи, могут быть
поверхности и более сложной конфигурации, особенно с увеличением числа
переменных. Но если работать в узкой области и оперировать набором двумерных
сечений, то рассмотренных случаев вполне достаточно, чтобы можно было построит
локальную модель и делать обоснованные
прогнозы. Наличие ПК и многочисленных программ по работе с многомерными
пространствами значительно облегчают техническую часть работы, но нет смысла
искать программу, чтобы можно было ввести экспериментальные результаты, нажать
кнопку, а далее списать готовый ответ. Хотя кое-кто рассчитывает именно на это.
Многие микроорганизмы растут на достаточно богатых
средах, содержащих гидролизаты и вытяжки из различного сырья природного
происхождения. Наиболее часто применяют гидролизаты растительного и животного
сырья и вытяжки из этих же источников, выдерживающие автоклавирование при
сохранении прозрачности без образования осадков, что необходимо для глубинного
культивирования но не обязательно для плотных питательных сред и сред для
хранения культур.
При конструировании синтетических питательных сред и
добавок заменяют компоненты питательных сред неизвестного или сложного состава
на смеси индивидуальных химических соединений меньшего разнообразия, либо
значительно снижают концентрации
неизвестных или вариабельных компонент.
Все компоненты питательных сред можно разбить на
достаточно независимые группы. Первая группа – неорганические компоненты. В
первую очередь макроэлементы. Это, прежде всего, соли фосфорной кислоты,
натрий, калий, магний, железо. Потом
необходимо отметить микроэлементы – сера, кобальт, никель, цинк, медь и
т.д. [16].
Следующий класс – органические соединения. На первом
месте – источники углерода, чаще всего – углеводы, сахароспирты, карбоновые
кислоты и липиды. Указанные соединения можно разбить на группы - необходимые, взаимозаменяемые, нейтральные,
не утилизируемые и токсичные. Методом полного или ограниченного перебора в серии
однофакторных экспериментов несложно обоснованно выбрать наилучшую добавку.
Углеводы утилизируются каждый по своей схеме и конкурируют между собой, обычно
глюкоза или фруктоза усваиваются в первую очередь. Углеводы нет смысла
проверять в смесях. Так же и карбоновые
кислоты. Нередко углеводы и карбоновые кислоты не конкурируют, а дополняют друг
друга, утилизируясь продуцентом по разным
биохимическим путям. Липиды тоже
могут не конкурировать с углеводами и карбоновыми кислотами и могут быть
заменены водорастворимыми твинами [2,16]. И уже на этой стадии серия
однофакторных экспериментов ограничена в своей пользе. Особых сложностей при
работе с этими компонентами нет. Особой чистоты прочих реактивов при их поиске
не требуется. Достаточно лишь быть уверенным в отсутствии потенциально
конкурирующих примесей, например отсутствие глюкозы в галактозе, химическая
чистота или известный состав жирных кислот и т.д.
На первой стадии наиболее простым шагом будет
использование минеральной основы, описанной для родственного микроорганизма, с
добавлением смесей аминокислот и витаминов и испытание разнообразных источников
углерода, при минимальных добавках компонент неизвестного или вариабельного
состава. Эта часть работы может быть выполнена по классической схеме как серия
однофакторных экспериментов. Но, если будет найдено, что желательно или
необходимо одновременное присутствие в среде как некоторого углевода, так и
какой - ни будь карбоновой кислоты и липида, то метод Зайделя - Гаусса приведет
к не всегда оправданной необходимости постановки большого количества
экспериментов.
Для хемоорганотрофов нужны соединения
азота в виде аминокислот и коротких пептидов, остающихся в растворимом виде
после автоклавирования (пептоны) [16]. Возможно позитивное влияние и биогенных
аминов (аспарагин, глутамин и т.д.). В большинстве случаев можно ограничиться
только набором наиболее распространенных индивидуальных 20 ти, хотя
в некоторых случаях пептиды могут быть регуляторными факторами при синтезе
конкретного ЦП. Аминокислоты могут требоваться не все, наиболее часто применяемые
20, а лишь некоторые. Для этого необходимо поставить многофакторный активный
отсеивающий эксперимент и выбрать минимальную группу аминокислот,
обеспечивающих нужный ВП.
При этом наиболее логично
фиксировать макро и микро элементы и источник витаминов, в большинстве случаев,
дрожжевой экстракт в разбавленном виде, чтобы уменьшить вклад аминокислот.
Иногда применяют какой – ни будь поливитаминный комплекс медицинского или
ветеринарного назначения, стерилизованный фильтрованием. Это более подходящий
вариант, поскольку не содержит собственных аминокислот и пептидов, шире по
содержанию витаминов, а возможные углеводы и прочие добавки можно учесть, либо
значительно уменьшить их влияние разбавлением.
После нахождения сильно действующих групп факторов
из разных классов, можно перейти к поиску многокомпонентной синтетической
добавки, уменьшая компоненты неизвестного состава и применяя отсеивающие
эксперименты по сверхнасыщенной схеме для большего количества факторов. Не
исключена сильная связь между компонентами питательной среды из разных классов
и при возможности это нужно проверить экспериментально. В руководстве
Максимова, Федорова [1] приведено много планов, позволяющих проверить до 32
факторов на 16 экспериментальных точках при обычной расстановке факторов и до
64 факторов при описанной выше расстановке двух факторов в одном столбце,
размещая каждый фактор на своем уровне (сверхнасыщенность второго типа).
Cочетаний факторов более высоких
порядков и не дает априорного преимущества ни одному из выбранных сочетаний факторов, по крайней мере для
уровня парных сочетаний. Это важно на первоначальном этапе работы, при
минимальной начальной информации, поиску, близкому к случайному, слабо
ограниченному какой-либо гипотезой или априорной информацией.. При этом
желательно рассмотреть максимальное количество качественно разнообразных
вариантов условий культивирования при минимальном количестве экспериментов.
Критерии разнообразия вариантов условий культивирования сформулировать
непросто, их можно принять на
интуитивном уровне.
Работа с
сериями питательных сред позволяет уменьшить систематическую ошибку при оценке
ВП и учесть сильное межфакторное взаимодействие между условиями
культивирования. Необходимость учета взаимодействия факторов становится особенно
ясной, если принять во внимание, что
отдельные факторы, не оказывающие сами по себе прямого влияния на урожай, могут
существенно влиять на него благодаря взаимодействию с другими факторами среды [1
– 5].
Очень важно,
что серия активных опытов по плану,
близкому к оптимальному, позволяет оценить тенденцию влияния того или иного
фактора или комбинации факторов на ВП. Это позволяет более рационально и
обоснованно ставить последующие эксперименты.
Таблица 1.
План трехуровневого переходного к оптимизации уточняющего
эксперимента.
|
1 |
А1 |
В1 |
С1 |
D1 |
E1 |
|
2 |
А1 |
В3 |
С2 |
D3 |
E2 |
|
3 |
А2 |
В3 |
С3 |
D2 |
E1 |
|
4 |
А2 |
В2 |
С1 |
D3 |
E3 |
|
5 |
А3 |
В1 |
С2 |
D2 |
E3 |
|
6 |
А3 |
В2 |
С3 |
D1 |
E2 |
В плане таб. 1 буквами
обозначены факторы, нижними индексами – уровни, парные сочетания факторов
присутствуют с одинаковыми частотами, хотя учтены не все, теоретически
возможные. План не единственный, но близкий к оптимальному согласно
сформулированным выше критериям.
Количество
экспериментов в серии в первую очередь зависит от стоимости каждого опыта. План
таб.11. можно расширить до 8 экспериментов (строк), добавляя эксперименты, в
которых все факторы находятся на одном уровне (все факторы на 2-ом и все
факторы на 3-ем уровнях). Такое расширение сохраняет учет парных сочетаний факторов, увеличивает количество учтенных
сочетаний факторов и увеличивает представленность сочетаний факторов более
высоких порядков, незначительно смещая частоты представленности сочетаний
факторов более высоких, чем парные, порядков. Наличие трех уровней варьирования
интенсивностей каждого фактора облегчает оценить тенденцию влияния фактора на
ВП, в отличие от двухуровневых планов. Наличие трех уровней варьирования
интенсивностей факторов позволяет более точно и надежно оценить тенденцию по
влиянию на синтез ЦП при большой ошибке измерений, что строго доказано
математиками ранее.
Поскольку при
многофакторном поиске можно говорить только о постановке серии экспериментов,
близкой к оптимальной, то выбор нужного плана во многом определяется стоимостью
каждого эксперимента. При невысокой стоимости есть смысл увеличивать количество
проверяемых факторов и экспериментов в одной серии до максимума. Постановка
серий экспериментов, объединенных одним временем и одним инокулятом, позволяет
повысить точность измерений ВП за счет уменьшения систематической ошибки и
временного дрейфа неконтролируемых воздействий при возможности выбора
внутреннего стандарта (опыта, принимаемого за эталон для сравнения).
Наличие ПК и
многочисленных прикладных программ по работе с многомерными пространствами
позволяют относительно несложно суммировать все проведенные наблюдения и
строить различные 2-х и3-х мерные
сечения поверхности отклика, облегчая исследователю представление вида
поверхности отклика в окрестности центра эксперимента, что значительно облегчит
планирование последующих серий опытов.
Ранжировку
строк в таблице по возрастанию (убыванию) некой величины автоматически
производят текстовые редакторы, перестановку столбцов таблицы тоже можно
сделать, не обращаясь к специализированным математическим программам. В крайнем
случае эту работу можно провести ручную
при помощи прозрачной пленки и фломастера, либо ножниц и клея.
Нахождение оптимальных условий синтеза
Оптимизация
биологического процесса сводится к экспериментальному отысканию условий, при
которых ВП достигает максимального значения. Подразумевается любая
характеристика процесса, представляющая интерес для экспериментатора (биомасса,
накопление какого-либо целевого продукта, представляющего экономический интерес
и т.д.). Условия протекания процесса определяются комплексом факторов, от
которых зависит его выход. В случае подбора оптимальных сред этот комплекс
включает в себя химический состав питательной
среды и условия культивирования организмов, такие как температура,
перемешивание, аэрация и т.д.[1].
Оптимизацию в
широком смысле слова следует проводить по всей совокупности факторов, влияющих
на ВП. В рамках рассматриваемых ниже методов не существует принципиальной
разницы между физически разнородными факторами по характеру их влияния на ВП,
вследствие чего можно одновременно проводить оптимизацию как состава среды, так
и условий культивирования. Однако на практике приходится сталкиваться с более
узкой задачей подбора оптимального состава сред при заданных условиях
культивирования или, иными словами, проводить оптимизацию по группе факторов
(например, химические компоненты среды) при постоянном уровне остальных
факторов [1]. В некотором смысле, это обобщение метода однофакторной
оптимизации, но в данном случае меняют одновременно несколько факторов на фоне
фиксированных остальных возможных переменных.
При этом
следует иметь в виду, что смена условий культивирования, как правило, приводит
к необходимости включения новых факторов в область управляемых или
контролируемых переменных. Увеличение ВП проводит к увеличению потребления
компонент, которые ранее считались малозначимыми. Наиболее рациональным для
оптимизации биологических объектов является
двухуровневые ПФЭ или ДФЭ, поскольку биологические процессы достаточно
длительны, ВП в большинстве случаев определяют биохимическими методами, что
делает нерентабельным использование
схем планирования типа симплекс - процедуры или случайного поиска, когда каждый
последующий шаг рассчитывают на основании результатов предыдущего. Достоинством
одновременной постановки большой серии опытов является и то, что появляется
возможность учета временного дрейфа за счет ведения внутренних эталонов для
каждой серии опытов, например, в простейшем случае, постановка опыта, в котором
все факторы находятся на верхнем (нижнем) уровне, либо берут некую “среднюю
точку” по интенсивностям (концентрациям).
Необходимым
моментом оптимизации является описание оптимальной области и условий, близких
к оптимуму. Возможно нахождение условного
экстремума, поэтому после нахождении оптимальных условий для некой группы
факторов, неплохо поставить новый ОЭ по группе факторов и убедится в их
незначимости или значимости и перейти к оптимизации по новой группе факторов.
Независимо от
конкретной схемы планирования, после нахождения оптимальной совокупности
существенных факторов, есть смысл в дополнительной проверке “несущественности”
тех факторов, которые были отсеяны на первых этапах. С этой целью после
нахождения некого оптимума может быть поставлен ОЭ на новом фиксированном уровне существенных факторов.
Стратегия такого поиска описана Максимовым и Федоровым [1].
После
нахождения группы сильнодействующих факторов и их активных уровней можно прейти
к оптимизации процесса. В качестве переходного исследования от ОЭ к
оптимизационному ПФЭ можно рекомендовать трехуровневый план таб.11, который
повышает надежность выбора факторов и их уровней для оптимизации процесса. При
проведении оптимизации с использованием
двухуровневых ПФЭ или ДФЭ следует учесть ряд ограничений этого хорошо известного метода [1,4].
Поверхность
отклика ВП в зависимости от интенсивностей управляемых переменных при
выращивании микроорганизмов имеет сложный многомерный вид, вообще говоря,
неизвестный экспериментатору. Функция отклика в зависимости от управляемых
переменных непредставима в виде достаточно простой и наглядной
алгебраической форме. Но в окрестности некой точки можно разложить любую сложную неизвестную функцию, описывающую
поверхность отклика, в ряд Тейлора по степеням
x, у (пример для случая
двух управляемых переменных).
(1) f(x,у) = a + вx +су + dxy + R(x,y)
/9/.
Поскольку
математика не дает возможности оценить величину остаточного члена R(x,y), то
приходится делать достаточно спорное предположение, что R(x,у) = 0 и
переходить к модели
(2)
f(x,y) = a + bx + cy + dxy ,
которая, вообще говоря, может быть и
неадекватной из-за неизбежного пренебрежения остаточным членом R(x,y), что является первым “подводным
камнем”.
В
уравнении (2) нужно определить неизвестные
a,b,c,d, располагая четырьмя измеренными значениями f(xi ,yi)
– ВП (1;..;4). Получается система из четырех линейных уравнений для
четырех переменных, которая может иметь
единственное решение.
Дадим
геометрическую интерпретацию уравнению (2). При фиксированных значениях f(x ,y)
= const (линии равного выхода) получаем
уравнения для различно ориентированных относительно осей х. и у
искаженных гипербол. Следовательно, в пространстве это могут быть -
гиперболический цилиндр (стационарное возвышение), либо гиперболический
параболоид (седловидная поверхность),
либо однополостный гиперболоид [9].
Уравнение (2)
в принципе не описывает поверхность типа параболоида или двухполостного гиперболоида, для этого в уравнении должны присутствовать новые
члены вида ех2 + fу2 , которые в дополнении к уравнению (2) для линий равного выхода
могут описывать семейство эллипсов, смещенных и разноориентированных
относительно начала координат, а в
пространстве описывают параболоид или двухполостный гиперболоид. Но именно
параболоид или двухполостный
гиперболоид (“шапочка”) наиболее
адекватно описывает поверхность отклика вблизи максимума. Следовательно, ДПФЭ - достаточно грубая модель, которую
следует воспринимать в большей
степени как информацию к размышлению, а не как однозначное и не подлежащее
сомнению руководство к действию.
Современные
достижения прикладной математики, наличие персональных компьютеров и
разнообразных доступных прикладных программ устраняют вычислительные проблемы,
но остаются принципиальные проблемы решения системы линейных уравнений с
неточными коэффициентами, так называемых плохо обусловленных систем (ПОСЛУ),
которые относятся к некорректно поставленным задачам [10,11].
ПОСЛУ – такая
система, при решении которой с конечной
(не важно какой) точностью,
появляются ложные решения, зависящие также от последовательности выбора
уравнений из системы при решении
методом подстановки [11]. Появление ложных решений связано с тем, что компьютер
(калькулятор) производит арифметические действия с конечной (не важно, какой)
точностью и в процессе вычислений накапливаются ошибки округления [10,11].
Другой источник неустойчивости решения ПОСЛУ – приближенные значения
коэффициентов при переменных как
эмпирических значений [11]. Один из путей регуляризации некорректно
поставленных задач – проверка вычисленных корней подстановкой [10]. Поэтому при
использовании программ для ПК следует отдать предпочтение тем программам, в которых при решении ПОСЛУ
предусмотрены автоматизированный перебор уравнений и подпрограмму по
автоматической проверке полученных решений подстановкой (проверка на
обусловленность). Не отрицается и интуитивный путь выбора истинного решения из
нескольких, предлагаемых компьютером [10],
полученных в результате различной последовательности выбора уравнений.
Кроме того,
ПОСЛУ с неточными коэффициентами сама по себе является некорректно поставленной
задачей, т.е. небольшое изменение начальных условий приводит к значительному
изменению решения, полученные решения неустойчивы. Рассмотрим пример,
описанный в литературе [13].
СЛУ (1)
х+10у = 11,1
10х+101у=111 решение системы (1) - х=11,1; у=0.
СЛУ (2)
х+10у=11
10х+101у=111 решение системы (2) - х=1; у=1.
Различия
свободных членов на 1% в первых
уравнениях систем (1) и (2)
приводят к сильному (более 100%)
изменению решений и при этом каждое решение для своей системы является
единственным и истинным. Увеличение числа уравнений и неизвестных
увеличивает неустойчивость
возможных решений.
Кроме этого,
если в уравнении (2) d=0, то получится
переопределенная СЛУ, в которой число
уравнений больше числа неизвестных.
Дадим
геометрическую интерпретацию. Как известно [9], система двух линейных уравнений
с двумя неизвестными может иметь единственное решение, геометрический смысл
которого - точка пересечения двух прямых
1 и 2 (рис.5).
У Рис.5
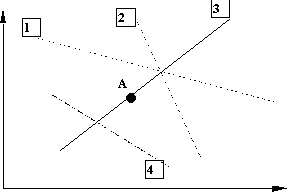
Х
Рисунок 5. Геометрическая интерпретация возможных решений переопределенной системы линейных уравнений.
В переопределенной СЛУ третье
уравнение описывает третью прямую -3
(рис.2), которая может совпадать с одной из двух первых, либо проходить через точку пересечения первых двух, но может проходить совсем в стороне – прямая 4 (рис.2).
При наличии ошибки, с которой задаются управляемые переменные х. и у, а
также ошибки измерения ВП, вокруг каждой прямой будет некий коридор ошибок.
Учитывая приблизительный характер самой модели, можно в качестве единственного
решения выбрать точку, равноудаленную ото всех прямых (точка А). Но пока эта
часть полностью принадлежит человеку и подобных программ для ПК еще нет.
Для ПФЭ 24 при использовании модели типа (2) получим 4 переменных для 16 уравнений, и
нахождение единственного решения приобретает не столько математический,
сколько философский смысл. Прикладная
математика обходит эту сложность тем, что программы для решения СЛУ на основе
ДПФЭ решают расширенную систему.
Например, для 4-х переменных и 16-ти экспериментов это будет система с 15-ю
неизвестными, расставленными по плану табл.6. Одну и ту же систему компьютер
будет решать для количества переменных
от 4 до 15-ти включительно, автоматически вводя фиктивные переменные сверх
выбранных экспериментатором при работе
с программами, в которых предусмотрено специализированное окно для
расчетов по плану ДПФЭ. Искусственно
введенные столбцы описывают взаимодействие факторов, каждая линейная комбинация
описывает свой набор взаимодействующих предшественников, подобно столбцам,
начиная с №5 таб.6.
Поскольку последующие столбцы являются линейной комбинацией первых, то
полученные уравнения будут описывать прямые, проходящие через общую
единственную точку, что доказывается в классических курсах по аналитической
геометрии. При использовании программ, рассчитанных на решение СЛУ без привязки
к ПФЭ, следует учесть этот момент. Решение СЛУ по результатам ПФЭ с применением
стандартных программ общего назначения необходимо проводить, самостоятельно
расширяя количество переменных за счет введения фиктивных, описывающих
взаимодействие факторов по правилу таб.5. Например, для ПФЭ 24 из 16 уравнений можно оставить 5, но это
можно сделать многими неоднозначными способами и получить несколько противоречащих
моделей, но можно расширить количество переменных до 15 ти взяв расширенный
план таб.6. Это позволит учесть и взаимодействие между факторами, часто встречающееся в микробиологии.
Поэтому, на наш взгляд, наиболее рационально до построения полиномиальной
модели провести обработку полученных
результатов измерений ВП наибольшим количеством способов - построение
корреляционных таблиц и полей, использование непараметрических критериев и т.д. [7]
для получения дополнительной информации, выделения сильно действующих факторов и обоснованно отбрасывая
незначимые факторы и их сочетания до расчета коэффициентов полинома. После
этого из обобщенной полиномиальной модели можно обоснованно построить модель со
значительно меньшим количеством переменных. Так в работе [12; 14] после
соответствующей обработки было оставлено 5 переменных из первоначально
подозреваемых 15. Последующие расчеты уточнили вид модели, и осталось только 3
члена. Такая предварительная обработка
позволяет обнаружить ложные решения, в которых коэффициенты полинома не
вписываются в допустимый коридор ограничений, полученный из применения
дополнительной информации на основе корреляционных таблиц и полей, без
значительного количества арифметических расчетов.
Поскольку ПОСЛУ с неточными
коэффициентами и конечной точностью вычислений относится к некорректно
поставленным задачам [10,11], то выбор наиболее адекватного решения
(регуляризация некорректно поставленной задачи) должен проводиться с использованием дополнительной информации [11].
При этом, чем больше уравнений, тем больше дополнительной информации можно
получить, используя статистические методы обработки полученной информации
до формулировки полиномиальной модели и решения СЛУ.
По нашему мнению, необходимо не менее 8 экспериментальных точек ( от 3х
до 7ми факторов, ДПФЭ 23), что позволяет построить
корреляционную таблицу, применить сериальный критерий с надежностью не менее
80% , а также метод парных сравнений, не требующие арифметических вычислений, а
только преобразования первоначального плана
корреляционную таблицу перестановкой строк и столбцов для увеличения наглядности и логического осмысления
результатов согласно разработанным математиками правилам (сериальный критерий,
метод парных сравнений). Увеличение количества подозреваемых переменных при
постановке первого ОЭ увеличивает вероятность успешного поиска не только из-за
увеличения количества проверяемых факторов, но и из-за повышения точности,
вызванной увеличением количества экспериментов
в серии, и независимых измерений ВП – преимущества применения пространства
высокой размерности. Одновременная постановка серии экспериментов позволяет
учесть возможный временной дрейф результатов измерений ВП, переходя к
относительным единицам и внутренним эталонам для каждой серии, позволяя точнее
сравнивать и использовать результаты различных серий.
Неустойчивость
решения СЛУ как модели ДПФЭ
следует также и из природы микробов,
поскольку одно или несколько из проверяемых переменных могут оказаться
регуляторными факторами для синтеза ЦП.
При наличии неконститутивного оперона
интенсивность синтеза целевого продукта может колебаться в десятки раз
при относительно небольших изменениях управляемых переменных (на десятки %), что выражается в сильной кривизне
поверхности отклика (зависимость ВП от управляемых переменных).
Исходя из
вышеизложенного, после постановки
ДПФЭ, не следует спешить с
вычислением “точных значений” коэффициентов полинома гиперболической модели
типа (2). Согласно нашему опыту, перспективнее
обработать результаты измерения ВП с применением метода парных сравнений и сериального
критерия. Хорошую информацию дает построение распределения ВП в зависимости от
номера эксперимента в ранжированном ряду, расчеты коэффициентов корреляции
рангов по нескольким критериям, построение нескольких корреляционных таблиц с
учетом ошибки измерения ВП и перестановкой перекрывающихся значений ВП в
ранжированных рядах, построение корреляционных полей.
Оправдывается
подход, при котором несколько низкоточных методов обработки результатов
измерений и рассмотрение альтернативных моделей оказываются более
конструктивным, чем применение одного высокоточного, поскольку высокая точность
вычислений коэффициентов полиномиальной
модели – кажущаяся, особенно при значительной ошибке измерений ВП, который в
случае химического эксперимента можно довести до нескольких процентов, а
микробиологический или медико-биологический - гораздо менее точный. Многие
измерения параметров бактериальной популяции проводятся с точностью 10 -20%,
что считается неплохим и близко к предельно возможной точности измерения в
бактериологии /16/. Нередко ошибку измерений вообще трудно оценить и приходится
пользоваться качественными оценками (например, реакция агглютинации или
диффузионной преципитации, другие иммунохимические измерения, кроме РИА и
ИФА и т.д.).
Если
сглаженная функция распределения ВП в зависимости от ранга эксперимента
представляет собой достаточно монотонную кривую типа 1 (рис.3), близкую к
обратно пропорциональной зависимости, то есть смысл искать коэффициенты
полинома гиперболической модели типа (2). Если указанное распределение имеет
более сложный вид типа кривой 2
(рис.3), то нужно разбивать выбранные факторы на более мелкие блоки и ставить
дополнительные эксперименты, хотя и в этом случае уже можно провести отсеивание
и сократить количество подозреваемых факторов. Наличие участков, близких к
горизонтальному, на распределении типа
2 (рис.6) отражает наличие почти эквивалентных сочетаний выбранных факторов.
Сложная зависимость ВП от номера эксперимента говорит о невозможности
применения полиномиальной модели, о неадекватности гиперболического приближения
поверхности отклика в изучаемой окрестности контролируемых факторов и
необходимости дополнительных экспериментов.
№Э 1 2 ВП Рис.6
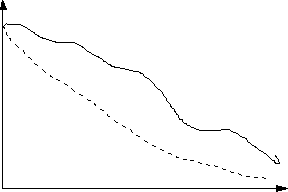
Возможные
зависимости выхода процесса от номера эксперимента в ранжированном ряду после
постановки серии опытов.
После анализа
полученной информации и доказательств адекватности гиперболической модели можно
провести качественную ранжировку
значимости факторов, обоснованно выбрать сильнодействующие, отбросить слабые
факторы и их сочетания и принимать решение о целесообразности и виде полиномиальной
модели. Получив несколько решений СЛУ, что быстро и несложно даже при
использовании ПК со слабыми процессорами, выбираем решения, наиболее
соответствующие полученной ранее информации.
Описанный
подход был использован при
изучении влияния условий
культивирования на антигенный состав
вакцины чумного микроба [12] и при изучении влияния условий культивирования на
синтез антигена F41 E.coli ВГНКИ 397А / 37-14 [8].
Постановка
ПФЭ 24 для изучения вакцины чумного микроба позволила в первой же
серии из 16 экспериментов найти условия, при которых пестицин и рН: – антиген
экспрессировались независимо при разных условиях культивирования. Это
согласуется с опубликованными ранее данными генетиков о том, что эти антигены
находятся в составе разных оперонов и
регулируются независимыми промоторно –
операторными участками. В сериях однофакторных экспериментов получить
такую информацию было бы крайне затруднительно. Но генетикам необходимо располагать данными физиологов, чтобы
строить модели регуляции экспрессии того или иного признака внешними условиями.
Для
продуцента диагностические важного проективного антигена F41
энтеропатогенной кишечной палочки после многофакторного поиска была
сконструирована среда, обеспечивающая более высокий уровень синтеза названного
антигена клетками. Это послужило основой для получения высокотитражной
специфической антисыворотки и значительно повысило надежность определения
указанного антигена в полевых штаммах, подозреваемых как возбудители
колидиаррей молодняка крупного рогатого скота. Такая информация позволяет обоснованно
провести эпизоотологический анализ вспышки инфекции и провести рациональную
терапию больных животных, в первую очередь – антибиотикотерапию. Возможность
наращивать штаммы с большим количеством протективного антигена служит основой
эффективного осуществления специфической вакцинопрофилактики.
Предлагаемый
подход с использованием семейства синтетических сред, составленных по близкому
к оптимальности плану из индивидуальных химических соединений разных классов,
учитывает только самую общую внутреннюю структуру живой системы, основан, прежде всего, на контроле внешних условий и изучении реакций системы. По нашему
мнению такой подход может быть обобщен не только на плохо изученные штаммы
микроорганизмов, но и для подбора и
оптимизации рационов у более организованных живых систем и иные выходы
процесса. Это следует из того, что регуляция активности оперонов условиями
окружающей среды едина у всех живых организмов [15].
Описанная
выше среда на основе пептона и лактозы обеспечивает синтез антигена F41 при глубинном культивировании, но работа в этом
направлении не была завершена, среда нигде не описана ранее. При применении
различных источников углерода в составе разработанной среды, возможно, наблюдать штаммоспецифичное
разнообразие экспрессии антигена, что происходит при эпизоотологическом анализе
распространения антигена F41 среди
изолятов кишечной палочки, выделенных из неблагополучных по колидиарреи
хозяйств. Эту работу проводили на базе бывшей фирмы “Диавак'' под
руководством Гусева В.В. и при помощи
Тазиной О.И. и Глазкова Н.К.
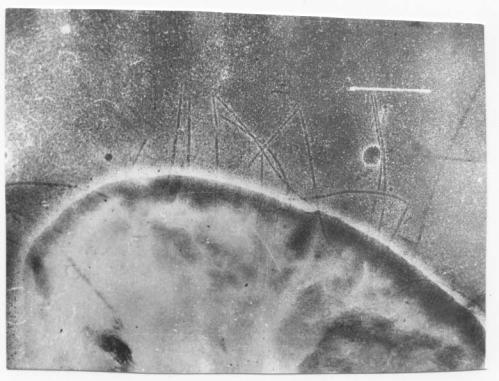
Фото 1. Вид клеток кишечной палочки
ВГНКИ 397А /37 - 14, выращенных на разработанной среде /10/ . Фимбрии
представлены в большом количестве и
достаточно наглядно. Белая черта на фото – 1 мкм. Для фото выбрана одна
из лучших клеток, поскольку разброс в
количестве фимбрий на клетку в популяции весьма велик.
Описанный подход многофакторного поиска был
использован при изучении влияния условий культивирования на
антигенный состав вакцины чумного
микроба /12/. Приводимые здесь
детали планирования и обработки ПФЭ не были опубликованы ранее в
силу специфики журнала /12/ и доложены
на конференции /14/. Постановка ПФЭ 24 для изучения вакцины чумного
микроба позволила в первой же серии из 16 экспериментов найти условия, при
которых пестицин и F – антиген экспрессировались независимо при разных условиях
культивирования, что согласуется с опубликованными ранее данными генетиков о
том, что эти антигены находятся в составе разных оперонов и регулируются независимыми промоторно –
операторными участками. В сериях однофакторных экспериментов получить такую
информацию было бы крайне затруднительно. А
генетикам необходимо располагать данными физиологов, чтобы строить модели
регуляции экспрессии того или иного признака конкретным продуцентом.
Таблица 2 (корреляционная).
|
№ранга |
№э |
КОЕ |
Объем среды, мл |
Показатель жизнеспособности |
||||||
|
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
||||
|
1 |
15 |
2 .5 |
100 |
|
|
|
Pst |
|
|
|
|
2 |
11 |
4 .7 |
100 |
|
|
|
|
|
|
|
|
3 |
16 |
3 .0 |
100 |
|
|
|
|
|
|
|
|
4 |
10 |
4.7 |
25 |
|
|
|
|
|
|
|
|
5 |
13 |
1 .4 |
25 |
РН6 |
|
|
|
|
|
|
|
6 |
6 |
2.0 |
25 |
|
РН6 |
|
|
|
|
|
|
7 |
9 |
2 .9 |
25 |
|
РН6 |
|
|
|
|
|
|
8 |
1 |
3 .6 |
25 |
|
|
РН6 |
|
|
|
|
|
9 |
2 |
2 4 |
25 |
|
|
РН6 |
|
|
|
|
|
10 |
14 |
3 .6 |
25 |
|
|
|
РН6 |
|
|
|
|
11 |
7 |
2 .9 |
100 |
|
|
|
Pst |
Pst |
|
|
|
12 |
8 |
3 .8 |
100 |
|
|
|
|
Pst |
|
|
|
13 |
12 |
3 .8 |
100 |
|
|
|
|
Pst |
|
|
|
14 |
3 |
4 .3 |
100 |
|
|
|
|
Pst |
|
|
|
15 |
4 |
4.3 |
100 |
|
|
|
|
|
Pst |
|
|
16 |
5 |
4.2 |
25 |
|
|
|
|
|
|
|
В таб. 2 рН6 обозначает антиген рН6, Pst – антиген пестицин.
Работу
проводили с вакцинным штаммом Y.pestis EV линии НИИЭГ. Влияние параметров культивирования и
состава питательных сред на синтез
антигенов изучали, используя план ПФЭ 24/1/. Корреляционная таблица
11 составлена перестановкой строк исходного плана по группировке антигенов рН6
и Pst. Жизнеспособность определяли как отношение КОЕ к оптической плотности
бактериальной суспензии, измеренной на красном фильтре ФЭК в кювете 1 см оптического пути.
Из представленных данных видно, что синтез
рН6 антигена коррелирует с повышенной аэрацией в объеме среды 25 мл на колбу
700 мл и пониженной жизнеспособностью популяции. Имеется одно “выскакивающее”
значение в опыте №13, которое можно объяснить промахом при постановке
эксперимента в виде пропущенной или лишней добавки.
Параметры,
стимулирующие синтез антигена Pst, находятся в области рН
7,0, объеме среды 100 мл, и повышенном показателе жизнеспособности. Уровни
показателей жизнеспособности клеток, продуцирующих названные антигены,
достоверно отличаются друг от друга. Одновременный синтез антигенов рН6 и Pst
наблюдали только в одном эксперименте, что, возможно, обусловлено неким
промахом при простановке серии опытов, что естественно в практической работе.
Синтез мышиного токсина и антигена F1 от условий культивирования
не зависел.
Полученные
данные подтверждают, что возможно управление процессом культивирования с целью
получения культуры, обогащенной определенным антигеном. Это упрощает дальнейшую
биохимическую очистку для получения чистых препаратов антигенов, используемых
для получения специфических антисывороток и при иммунохимических реакциях с изучаемой культурой.
Ранжировка результатов ПФЭ по уровням концентраций клеток и применения
вышеуказанных распределений (данные не приведены) показало, что основными
факторами, влияющими на общее
количество клеток, являются концентрация галактозы, совместное действие рН и
аминного азота и совместное действие галактозы и аминного азота. Согласно этому
были проведены количественные расчеты, которые подтвердили, что именно эти
параметры влияют на рост культуры. При этом зависимость нелинейная и
определяется, прежде всего, взаимодействием факторов.
Приведенные экспериментальные данные демонстрируют,
что только использование многофакторного эксперимента позволило решить задачи
поиска регуляторных факторов для указанных выше культур. В серии однофакторных
экспериментов этого бы сделать либо вовсе не удалось, либо удалось бы с
большими трудозатратами и
непредсказуемым везением.
Использование плана многофакторного поиска, близкого
к оптимальному, позволило быстро найти минимальную группу регуляторных факторов
среди достаточно большого множества подозреваемых и в первой же серии оценить
тенденцию влияния найденных факторов и их концентраций (интенсивностей) на ВП,
что позволило осознанно поставить следующие эксперименты при относительно
небольших трудозатратах.
Классификация проверяемых факторов на сильно
действующие (позитивные, индукторы), нейтральные и токсичные (ингибиторы,
корепрессоры) позволяет объединять их в достаточно большие группы и ставить
серийные эксперименты по сверхнасыщенной схеме, когда количество проверяемых
факторов превышает количество единичных испытаний. При этом возможно получить
несложно трактуемые результаты без значительных арифметических вычислений и
обоснованно поставить следующую серию поиска сильнодействующих факторов, либо перейти
к нахождению оптимального соотношения выделенных сильно действующих факторов,
если их количество сократилось до некого приемлемого уровня.
Можно
считать приемлемым количеством 4- 5 выделенных факторов. Тогда ПФЭ 24 это 16 опытов, в 2 повторностях – 32 опыта и
при работе с колбами – вполне реальные цифры. Для 5 факторов соответственно 32
и 64 эксперимента, что тоже реально, либо те же 16 и 32, если ставить ДФЭ 25-1 , выбрав некое сочетание факторов незначимым
на основании предварительных испытаний.
Контурно-графический анализ результатов измерений
Для
обработки результатов экспериментов с минимальным количеством арифметических
вычислений можно использовать контурно-графический анализ Клейнмана и
Берча [цит. по 18]. Сущность его состоит в упорядоченном
расположении опытов в факторном пространстве путем построения графических
зависимостей ВП от управляемых переменных в виде двумерных сечений поверхности
отклика. Получение дополнительной информации происходит путем линейной
экстраполяции графических зависимостей через
построение на двумерных сечениях
поверхности отклика линий постоянного уровня ВП в зависимости от концентрации
(интенсивности) разнообразных парных
выборок факторов.
Х
Рис.6. Контурно-графический метод
Методами
контурно-графического анализа можно строить на кальке контурные линии различных
сечений функции отклика, характеризующей процесс. Совмещая координатные оси
этих графиков, и просматривая кальки на просвет, можно достаточно быстро
выбрать оптимальные условия ведения процесса. Работа не сложная и не связана с
большим количеством арифметических вычислений. Недостаток этого метода –
необходимость располагать большим количеством экспериментальных точек,
измеренных с высокой точностью. Однако при решении задач по увеличению выхода
биомассы, когда работа идет с чашками или пробирками, когда проще засеять
несколько десятков проб, несложно набрать необходимую статистику и обеспечить приемлемую
точность измерения ВП при минимальных арифметических вычислениях. При этом
отпадает необходимость глубоко анализировать небольшое количество измерений с
помощью разных статистических методов, не всегда понятных экспериментатору.
Схемы
Берча и Клейнмана не исчерпывают всех возможных вариантов расположения
экспериментальных точек в факторном пространстве. Следует иметь в виду, что
расстояние между экспериментальными точками не должно быть слишком большим. В
противном случае при значительной кривизне и сложной форме поверхности отклика
неизбежные погрешности линейной экстраполяции могут отрицательно сказаться на
разработку возможных прогнозов.
Заключение
Описанный
выше подход основан на минимальном знании внутренней структуры изучаемого
объекта, в первую очередь генетики и физиологии, и
предназначен быть базой, как для изучения (построения) частной физиологии, так
и частной генетики живой системы. Этот подход оперирует в основном
контролем внешних условий и измерением реакций системы, не обязательно с
высокой точностью. Допускается использование
качественных и экспертных оценок, что
важно при сложных реакциях мало изученной системы. В ряде случаев можно
обойтись отображением результатов измерений
в виде графиков, корреляционных таблиц и полей при минимуме
арифметических вычислений. По нашему мнению, такой подход может быть
применим и к системам более высокой, чем микробы, организации и более сложным
синтезам. Поскольку ВП в большинстве случаев измеряют с применением химических
методов, то и для чисто химических процессов такой подход тоже применим,
особенно для задач поиска условий кристаллизации или ферментативной активности.
В органической химии исследователи оперируют в большинстве случаев небольшим
количеством переменных. В таком случае можно ограничится планами на уровне
ДФЭ, трехуровнего плана таб.11 и ПФЭ.
Просьба замечания и предложения отправлять по olkoshu@rambler.ru.
Литература
1.
Максимов
В.Н., Федоров В.Д., Применение методов математического планирования
эксперимента при отыскании оптимальных условий культивирования микроорганизмов.
М.,МГУ.,1969., 125 с.
2.
Ленинджер
А.,Биохимия., М., “Мир”., 1874., 956 с.
3.
Стейнер
Р., Эдельберг Э., Ингрэм Дж., Мир микробов., т.1., М., “Мир” 1979.,320 с.
4.
Максимов
В.Н., Многофакторный эксперимент в биологии. М.,МГУ.,1983. 452с.
5.
Шулюпин
О.К. Критерии оценки оптимальности отсеивающих экспериментов. Депонированная
рукопись. НПО “Медбиоэкономика” 17.11.88. реферат опубликован в
библиографическом указателе ВИНИТИ “Депонированные научные работы” 1989г,№ 3,
стр.115.
6.
Morris J.A., Thorng C., Scott A.C., Adhesion in
vitro and in vivo associated with an adhesive antigen (F41) produced by a K99
mutant of the reference strain E.coli
B41. Inf. Imm. 1982. V.38. № 3, р.1148-1153.
7.
Архипов
Г.П., Лаврова И.Г., Трошина И.М., Некоторые современные методы статистического
анализа в медицине., М. “Медицина”. 1971., 123 с.
8.
Шулюпин
О.К., Светоч Э.А., Жиленков Е.Л., Гусев В.В., Тугаринов О.А., Малахов Ю.А.,
Питательная среда для выявления фимбриального антигена адгезии F41.
Патент SU 1720652., 23.03.1992 г. Бюл.№11., 4 с.
9.
Корн
Г., Корн Т., Справочник по математике. М. “Наука”. ГРФМ. 1984.831с.
10.
Эберт
К., Эдерер Х. Компьютеры, применение в
химии. М.“Мир”.1988. 264с.
11.
10. Тихонов А.Н., Уфимцев М.В.,
Статистическая обработка результатов экспериментов. М. МГУ. 1988. 135 с.
12.
Гремякова
Т.А., Степаншина В.Н., Шулюпин О.К., Негрий В.Ф., Мицевич Е.В., Экспрессия
основных антигенов и ростовые свойства клеток
Yersinia pestis в средах различного состава
при 370С. ЖМЭИ. 1993., № 1,с.16-20.
13.
Хургин
Я.И. Да, нет, или может быть. М. “Наука”. ГРФМЛ.1983. 206 с.
14.
Шулюпин
О.К. Проведение работ по поиску условий культивирования, влияющих на синтез
микроорганизмами значимого продукта. Пущино. 20007 г. 11-я международная
Пущинская школа-конференция. Сборник тезисов.331 с.
15. Уотсон Дж.
Молекулярная биология гена. М. Мир. 1978. 456 с.
16.Мейнелл Дж., Мейнелл Э.
Экспериментальная микробиология. М. Мир , 1967.345 с.
17. Martin, J.E.< et al/1967/Public Health Rep. 82 361.
18.Саутин С.Н. Планирование эксперимента в химии и
химической технологии. “Химия”. 1975.48 с.
Пущино
Поступила в редакцию 25.01.2011.