Будаев В

УДК 517.927.25+517.98

Спецкурс

ОСНОВЫ СПЕКТРАЛЬНОЙ ТЕОРИИ НЕСАМОСОПРЯЖЕНЫХ

ДИФФЕРЕНЦИАЛЬНЫХ ОПЕРАТОРОВ*

ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНОГО АНАЛИЗА

В этой главе излагаются некоторые сведения из функционального анализа, необходимые для понимания основной части спецкурса.

В целях доступности изложения для нематематиков основные понятия достаточно подробно объясняются. Однако для математиков (в частности, для аспирантов и студентов старших курсов) желательно предварительное знакомство с классическими курсами математического анализа и линейной алгебры, а также теорией интеграла Лебега.

1. Линейные пространства. Базис

Одно из основных понятий современной математики - линейное пространство.

Пусть L - некоторое множество объектов произвольной природы, а C - множество комплексных чисел. Множество L называют линейным пространством, если на нем определены две операции: 1) операция сложения любых двух элементов этого множества и 2) операция умножения элементов этого множества на комплексное число, причем эти операции удовлетворяют некоторым естественным аксиомам. Более точно:

Определение. Множество L называется линейным пространством над полем комплексных чисел C, если

каждой паре элементов x, y из этого пространства поставлен в соответствие элемент z этого пространства, называемый суммой элементов x и y (обозначение: );
каждому элементу x из L и каждому комплексному числу поставлен в соответствие элемент из L, называемый произведением и x (и обозначаемый или x);
указанные операции удовлетворяют следующим аксиомам:
для любых ,
для любых ,
существует "нулевой" элемент , такой, что для любого ,
для каждого существует "противоположный" ему элемент , такой, что ,
для любого ,
для любого и любых ,
для любого и любых ,
для любого и любых .

Подчеркнем, что перечисленные аксиомы являются естественным обобщением хорошо известных свойств сложения и умножения чисел, сложения векторов и их умножения на число и т.д.

Иногда рассматривают линейное пространство не над полем комплексных, а над полем действительных чисел R (т.е. вместо операции умножения на комплексные числа рассматривается операция умножения на действительные числа). Аксиомы линейного пространства при этом не меняются.

Приведем некоторые типичные примеры линейных пространств.

Пример 1. Линейное пространство векторов на плоскости (или в трехмерном пространстве) с обычными операциями сложения векторов и умножения вектора на действительное число. Нулевым элементом является нулевой вектор.

Пример 2. Линейное пространство всевозможных последовательностей комплексных чисел с операциями

Нулевой элемент - последовательность (0, 0, ..., 0, ...).

Пример 3. Линейное пространство функций, непрерывных на данном отрезке с обычными операциями сложения функций и умножения функции на действительное число. Нулевой элемент - функция .

Пример 4. Линейное пространство всех комплекснозначных функций , где и непрерывны на с обычными операциями сложения функций и умножения функции на комплексное число. Нулевой элемент - функция .

Заметим, что в примерах 1, 3 рассмотрены линейные пространства над полем действительных чисел R, а в примерах 2, 4 - над полем комплексных чисел C. Выполнение всех 8 аксиом в каждом из примеров очевидно.

Пусть теперь - некоторые элементы линейного пространства L, а - произвольные комплексные (или действительные) числа. Элемент пространства L, равный , называется линейной комбинацией элементов .

Определение. Система (набор) элементов пространства L называется линейно независимой, если линейная комбинация равна нулевому элементу пространства только в случае .

Иными словами, система называется линейно независимой, если из равенства следует, что .

Определение. Система элементов пространства L называется линейно зависимой, если равенство выполнено при некотором наборе констант , хотя бы одна из которых отлична от нуля.

Таким образом, система называется линейно зависимой, если она не является линейно независимой.

Так, в пространстве непрерывных функций (действительных; на любом промежутке) система функций линейно зависима, поскольку , а система функций при любом натуральном n линейно независима, т.к. линейная комбинация представляет собой многочлен, а из алгебры известно, что многочлен тождественно равен нулю тогда и только тогда, когда все его коэффициенты нулевые.

Естественно поставить вопрос: сколько элементов может содержать линейно независимая система в том или ином линейном пространстве? Очевидно, что в пространстве векторов на плоскости можно указать систему из двух линейно независимых векторов (это могут быть любые 2 неколлинеарных вектора), но уже любые 3 вектора - линейно зависимы. Естественно назвать такое пространство двухмерным. В то же время в пространстве непрерывных функций , как мы видим, можно указать любое наперед заданное число линейно независимых функций. Такое пространство естественно назвать бесконечномерным.

Определение. Линейное пространство имеет размерность n (или, коротко, n-мерно), если в нем найдется n линейно независимых элементов, но любые (n+1) элемент линейно зависимы. Линейное пространство называется бесконечномерным, если в нем можно указать любое наперед заданное число линейно независимых элементов.

Пространства, рассмотренные выше в примерах 2-4 - бесконечномерны.

Пусть теперь L - n-мерное линейное пространство. По определению, в нем существует набор линейно независимых элементов. Если f - произвольный элемент из L, то система линейно зависима, т.к. содержит (n+1) элемент. Значит, найдется набор констант , хотя бы одна из которых отлична от нуля, такой, что

Очевидно, (в противном случае система оказалась бы линейно зависимой). Тогда

т.е. элемент f оказался представленным в виде линейной комбинации элементов линейно независимой системы.

Убедимся, что такое представление единственно. В самом деле, пусть элемент f можно представить двумя способами в виде линейной комбинации элементов системы :

и .

Тогда

В правой части мы получим линейную комбинацию элементов линейно независимой системы. Из равенства этой линейной комбинации нулю следует равенство нулю всех коэффициентов. Таким образом, , т.е. два представления элемента f оказались совпадающими.

Мы пришли к следующему выводу: любой элемент n-мерного линейного пространства можно представить (причем единственным способом) в виде линейной комбинации произвольных n элементов, образующих линейно независимую систему. Этот факт весьма важен: в самом деле, n элементов линейно независимой системы в n-мерном пространстве оказываются теми "кирпичиками", из которых можно сложить абсолютно любой элемент пространства. В силу важности этого факта введем специальное понятие - базис линейного пространства.

Определение. Система элементов линейного пространства называется базисом этого пространства, если любой элемент этого пространства можно единственным образом представить в виде линейной комбинации элементов данной системы.

Как мы убедились, в n-мерном пространстве любая линейно независимая система из n элементов образует базис.

Естественно поставить вопрос: справедливо ли аналогичное утверждение для бесконечномерных пространств, и что вообще представляет собой базис бесконечномерного пространства?

Само по себе сформулированное выше определение базиса никак не привязано к размерности пространства, поэтому формально такое определение годится и для бесконечномерного пространства. Однако здесь сразу возникают некоторые проблемы. В самом деле, базис бесконечномерного пространства, очевидно, не может состоять из конечного числа элементов, это должна быть бесконечная система. Но что понимать под "линейной комбинацией бесконечного числа элементов"? Понятие линейной комбинации введено нами лишь для конечного числа элементов; более того, аксиомы линейного пространства позволяют рассматривать сумму любого конечного числа слагаемых, но никак не определяют сумму бесконечного числа слагаемых. Наконец, если мы даже определим бесконечную сумму (и, соответственно, бесконечную линейную комбинацию), то в каком смысле следует понимать равенство этой бесконечной суммы некоторому элементу пространства?

Таким образом, изучение базисов в бесконечномерных линейных пространствах немыслимо без рассмотрения бесконечных сумм (которые, как и в классическом анализе, будем называть рядами). Изучение рядов, как и любых математических объектов, связанных с бесконечностью, невозможно без введения в том или ином виде понятия предела (так, в классическом анализе сумма числового ряда понимается как предел частичных сумм этого ряда). А понятие предела, в свою очередь, предполагает возможность тем или иным образом оценить "близость" друг к другу элементов пространства (так, классическое понятие предела числовой последовательности фактически означает, что члены последовательности все ближе и ближе приближаются к некоторому фиксированному числу, называемому пределом этой последовательности). Тем самым возникает необходимость во введении такого понятия, как расстояние между элементами пространства. Иными словами, пространство должно быть наделено метрикой.

Мы пришли к еще одному чрезвычайно важному выводу: изучение бесконечномерных линейных пространств (точнее, рассмотрение базисов в этих пространствах) невозможно лишь в терминах самого линейного пространства, но требует введения некой метрики. Таким образом, рассматриваемое пространство должно быть наделено не только линейной, но и метрической структурой. В этом заключается коренное отличие бесконечномерных линейных пространств от конечномерных.

2. Метрические и нормированные пространства.

Банаховы пространства

Определение. Множество M называется метрическим пространством, если каждым двум элементам x, y этого множества поставлено в соответствие действительное число, обозначаемое и называемое расстоянием между элементами x и y, причем выполнены следующие аксиомы:

для любых , причем в том и только в том случае, когда ;
для любых ;
для любых .

Если x, y - два фиксированных элемента множества M, то есть действительное число, однако, полагая x и y равными всевозможным элементам множества M, получим, что является функцией двух переменных x, y. Эта функция называется метрикой данного пространства.

Любое множество можно наделить метрикой: например, достаточно положить 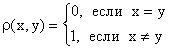. Примером метрического пространства может также служить множество точек плоскости, где расстояние между точками и определяется как . При этом третья аксиома, принимающая вид (где A, B, C - произвольные точки плоскости) имеет наглядную интерпретацию: длина любой из сторон треугольника не превосходит суммы двух других сторон (равенство достигается, если треугольник "вырожден": точка C лежит на отрезке AB). В связи с этим третью аксиому метрического пространства часто называют неравенством треугольника.

Приведем теперь менее тривиальный пример. В пространстве непрерывных на отрезке функций (действительных или комплексных) введем метрику

Выполнение первых двух аксиом метрического пространства при этом очевидно, а выполнение третьей аксиомы следует из тривиальных свойств модуля и того факта, что максимум суммы не превосходит суммы максимумов:

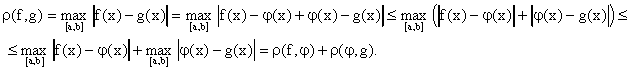
Разумеется, на одном и том же множестве метрику можно ввести по-разному. Рассмотренная только что метрика в пространстве непрерывных функций называется равномерной метрикой (пространство с этой метрикой обозначают ). Однако на том же самом множестве непрерывных функций можно ввести и так называемую среднеквадратичную метрику

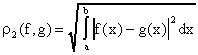
(пространство с этой метрикой обозначают ), и некоторые другие метрики. Выполнение неравенства треугольника для среднеквадратичной метрики будет доказано несколько позже.

В линейных пространствах наряду с метрикой используют понятие нормы элемента.

Определение. Линейное пространство называется нормированным, если каждому элементу x этого пространства поставлено в соответствие действительное число (норма x ), причем выполнены следующие аксиомы:

для любого x, причем тогда и только тогда, когда ;
для любого x и любого комплексного ;
для любых x, y из данного пространства.

Для линейных пространств над полем действительных чисел также вводится понятие нормированного пространства с теми же аксиомами.

Неравенство, фигурирующее в третьей аксиоме, называется неравенством Минковского.

Простейшими примерами нормированных пространств могут служить множества действительных чисел R и комплексных чисел C, где в качестве нормы числа рассматривается его модуль, а также пространство векторов на плоскости (или в пространстве) с нормой, равной длине вектора.

В пространстве непрерывных функций на (действительном или комплексном) норму можно ввести, например, следующими способами:

, .

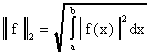
Отметим теперь следующий важный факт. В любом линейном нормированном пространстве можно ввести метрику следующим образом:

При этом выполнение первой аксиомы метрического пространства следует из первой аксиомы нормированного пространства. Выполнение второй аксиомы также очевидно:

Наконец, выполнение третьей аксиомы метрического пространства следует из неравенства Минковского:

Итак, любое линейное нормированное пространство можно сделать метрическим пространством указанным выше естественным способом (так, указанные нами нормы в пространстве непрерывных функций порождают соответственно равномерную и среднеквадратичную метрику, т.е. порождают пространства и соответственно). Обратное утверждение, вообще говоря, неверно: не в любом метрическом пространстве можно ввести норму, поскольку понятие нормы вводится лишь в линейном пространстве, а метрическое пространство может не быть наделено линейной структурой. Однако, если метрическое пространство наделено линейной структурой (является линейным пространством), то его всегда можно сделать нормированным, введя норму

Всюду в дальнейшем мы будем рассматривать исключительно линейные нормированные пространства, причем всюду (в случае необходимости) будем подразумевать, что пространство снабжено естественной (индуцированной) метрикой .

Пусть теперь - некоторая последовательность элементов линейного нормированного пространства L, а - некоторый фиксированный элемент L. Для каждого номера n найдем . Тем самым получим числовую последовательность .

Определение. Элемент линейного нормированного пространства L называется пределом последовательности элементов , если

(или ).

Обозначение: (если необходимо, то указывают, по какой норме рассматривается предел).

Если последовательность имеет предел, то она называется сходящейся (по норме данного пространства), в противном случае - расходящейся.

Пример. Рассмотрим последовательность функций в пространстве . Функция является ее пределом, т.к.

при .

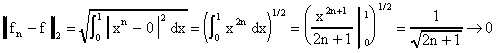
Однако в пространстве эта же самая последовательность расходится. Действительно, допустим, что в равномерной метрике. Тогда

При каждом фиксированном

очевидно,

и, следовательно,

, т.е.

Но .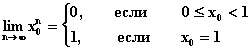

Итак, 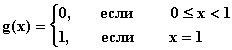. Однако такая функция не является непрерывной на , т.е. вообще не принадлежит рассматриваемому пространству. Таким образом, в данная последовательность предела не имеет.

Как видим, одна и та же последовательность может иметь предел в одной метрике и не иметь в другой.

Если последовательность имеет предел, то этот предел единственен. В самом деле, пусть и . Тогда

При правая часть стремится к нулю, следовательно, левая часть также стремится к нулю. Но - константа, поэтому =0, а значит, .

Определение предела последовательности элементов нормированного пространства основано на понятии предела числовой последовательности. Используя определение предела числовой последовательности, "расшифруем" более подробно понятие предела в нормированном пространстве.

Элемент линейного нормированного пространства L является пределом последовательности элементов , если для любого (сколь угодно малого) найдется номер N, такой, что для всех номеров n, больших N, выполнено неравенство . Или, в символьной записи,

Рассмотрим теперь понятие фундаментальной последовательности, тесно связанные с понятием предела.

Определение. Последовательность элементов линейного нормированного пространства называется фундаментальной, если

Очевидно, что любая сходящаяся последовательность фундаментальна: если , то

тогда для всех номеров что и доказывает фундаментальность последовательности .

Из курса анализа известен критерий Коши: числовая последовательность сходится тогда и только тогда, когда она фундаментальна. Иными словами, пространство R устроено так, что в нем не только из сходимости следует фундаментальность, но и наоборот. Однако не любое линейное нормированное пространство устроено таким образом: например, в пространстве рациональных чисел Q (с обычными линейными операциями и нормой ) фундаментальная последовательность может расходиться (такая ситуация имеет место, если пределом последовательности рациональных чисел является число иррациональное).

Определение. Линейное нормированное пространство называется полным, если в нем любая фундаментальная последовательность сходится.

Полное линейное нормированное пространство называют также банаховым пространством (по имени выдающегося польско-украинского математика Стефана Банаха (1892-1945)).

Пространства R и C - банаховы, а пространство Q - нет.

Рассмотренное выше пространство - банахово. В самом деле, пусть - фундаментальная последовательность в .

Тогда ( Тогда для любого фиксированного , причем номер N не зависит от x. По критерию Коши равномерной сходимости это означает равномерную сходимость последовательности .

Переходя в неравенстве к пределу при , получим: , откуда следует, что , что означает сходимость последовательности к по норме . Таким образом, пространство - полное, а значит - банахово.

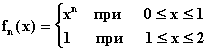
Любопытно, что пространство полным не является. В качестве примера рассмотрим в последовательность . Предположим, что некоторая непрерывная функция f(x) является пределом этой последовательности в метрике .

Очевидно, 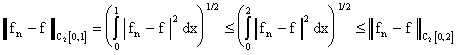, а следовательно, если сходится к f(x) в метрике , то сходится и в метрике . Однако, на отрезке [0, 1] рассматриваемая последовательность совпадает с рассмотренной выше последовательностью и имеет своим пределом в функцию, тождественно равную нулю. Аналогично, f(x) является пределом в , а поскольку на [1, 2], то и предел этой последовательности в тождественно равен 1. В силу единственности предела, получаем, что на [0, 1] и на [1, 2] и при этом f(x) непрерывна на [0, 2]. Очевидно, таких функций не существует. Следовательно, последовательность в расходится. Вместе с тем

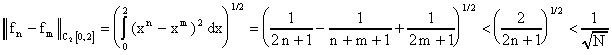
при n, m > N. Выбирая для произвольного фиксированного номер , убеждаемся в фундаментальности данной последовательности в .

Построенный пример легко обобщается с отрезка [0, 2] на произвольный отрезок [a, b]. Итак, пространство неполно.

3. Пространства Лебега

Рассмотрим один важнейший вид банаховых пространств.

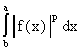
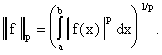
Зафиксируем действительное число и некоторый отрезок [a, b]. Рассмотрим на [a, b] множество всех комплекнозначных функций f(x), для которых существует . Операции сложения функций и умножения функции на комплексное число определим обычным образом. Норму определим как

Полученные таким образом пространства (ниже мы убедимся, что эти пространства банаховы при любом ) называют лебеговыми пространствами или классами Лебега** и обозначают

Вообще говоря, в современной математике используются несколько различных понятий определенного интеграла. Наиболее употребимыми из них являются интеграл Римана (именно его обычно изучают в классическом курсе анализа) и интеграл Лебега. Как явствует из самого названия, при рассмотрении классов Лебега используется интеграл Лебега.

К сожалению, понятие интеграла Лебега незнакомо даже большинству студентов физматов пединститутов. В связи с этим, для математиков, изучающий данный спецкурс и незнакомых с интегралом Лебега, предлагается следующий порядок действий: при первом чтении не слишком вдаваться в тонкости отличия интегралов Римана и Лебега
(ограничившись сделанными ниже замечаниями), а затем, после чтения спецкурса, заняться основательным изучением интеграла Лебега, после чего вернуться к повторному чтению соответствующих разделов спецкурса.

Пока же рекомендуем лишь обратить внимание на следующее:

1. Понятие интеграла Лебега - более общее, чем интеграла Римана. Функция, интегрируемая на [a, b] по Риману, интегрируема и по Лебегу (причем значения интегралов совпадают), но обратное, вообще говоря, неверно.

2. В теории интеграла Лебега функции, отличающиеся лишь на множестве меры нуль (в частности, на конечном или счетном множестве точек), считают эквивалентными (т.е. фактически неотличимы друг от друга) и интегралы от таких функций равны. Так, например, функции на [0, 1], и

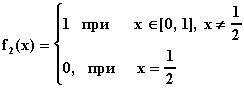
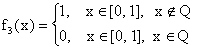
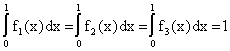
(функция Дирихле) эквивалентны; все они интегрируемы по Лебегу и . Таким образом, элементами классов фактически являются не отдельные функции, а классы эквивалентных функций. Например, функции принадлежат пространству (а также любому пространству ) и представляют собой один и тот же элемент этого пространства: этот элемент является множеством всех функций, эквивалентных на [0, 1] функции, тождественно равной 1.

3. Интеграл Лебега обладает некоторыми весьма удобными свойствами, не присущими интегралу Римана, в частности: если на [a, b] и g(x) интегрируема на [a, b] то f(x) также интегрируема на [a, b]; функция интегрируема на [a, b] тогда и только тогда, когда интегрируем ее модуль (при этом, правда, требуется измеримость рассматриваемых функций, на чем мы сейчас не будем останавливаться).

Иногда, чтобы отличать интеграл Лебега от интеграла Римана, вместо термина "функция интегрируема по Лебегу" используют термин "функция суммируема".

Вернемся теперь к пространству . Убедимся, что - линейное пространство и что введенная нами норма действительно удовлетворяет аксиомам нормы.

Выполнение аксиом линейного пространства очевидно, за исключением того факта, что если и , то и , где . Для доказательства этого факта обозначим через A множество всех тех точек интервала (a, b), в которых , а через В - точек, в которых . Для читателей, знакомых с интегралом Лебега, подчеркнем, что множества А и В измеримы. Введем функцию . Очевидно, что существует, поскольку , а последние два интеграла по условию существуют. Далее, . 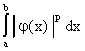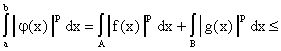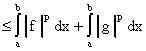Соответственно, . Из интегрируемости правой части следует интегрируемость левой, что и доказывает тот факт, что .

Проверим теперь выполнение аксиом нормы.

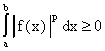
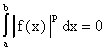
Поскольку то, по свойствам интеграла, и, значит, . Пусть , т.е. . Покажем, что на [a, b]. Возьмем произвольное . Обозначим через подмножество отрезка [a, b], состоящее из всех x, для которых

. Если (где - лебегова мера множества , то

, что противоречит условию . Следовательно, для любого имеем Пусть теперь - подмножество [a, b], на котором . Очевидно, Но тогда , т.к. является счетным объединением множеств меры нуль. Таким образом, f(x) = 0 на [a, b] почти всюду (т.е. за исключением множества меры нуль). Итак, если , то f(x) эквивалентна тождественно нулевой функции, т.е. первая аксиома нормы выполнена.

Выполнение второй аксиомы очевидно.

Для доказательства справедливости третьей аксиомы (неравенство Минковского) установим некоторые вспомогательные неравенства.

Пусть p > 1, q - действительное число, удовлетворяющее условию (т.е. ), числа - произвольные.

Докажем, что

(1) .

Рассмотрим функцию на при фиксированных a, p, q. Поскольку , то, как нетрудно убедиться, принимает наименьшее значение при . Это наименьшее значение равно

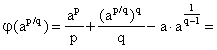
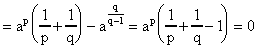
Следовательно, на , что доказывает неравенство (1).

Пусть снова Пространства и называют взаимно сопряженными. Возьмем , , причем , . Используем неравенство (1) при , при каждом фиксированном :

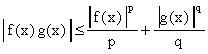
Правая часть интегрируема, следовательно, по свойствам интеграла Лебега, интегрируема и левая часть. Проинтегрируем по [a, b]:

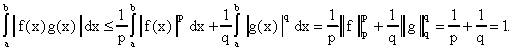
Итак, если и , то

(2) .

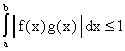
Пусть, далее, (без ограничений на их норму). Используем (2) для функций и , нормы которых в и соответственно равны 1. Получим

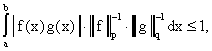
или

(3)

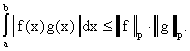
Поскольку модуль интеграла не превосходит интеграла от модуля, то

(4)

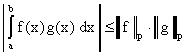
Неравенство (4) называется неравенством Гельдера и играет огромную роль в функциональном анализе. Его частный случай при (при этом ) называется неравенством Коши-Буняковского (в западной литературе - неравенством Шварца).

Перейдем теперь непосредственно к доказательству неравенства Минковского, т.е. неравенства

(5)

для любых и любого . Очевидно,

Проинтегрируем обе части по и применим к каждому из слагаемых в правой части неравенство Гельдера:

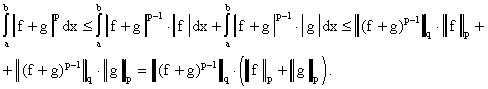
Поскольку , то

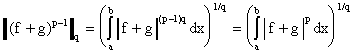
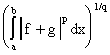
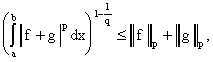
Деля обе части неравенства (6) на , получим

откуда, учитывая, что , приходим к неравенству Минковского.

Итак, все аксиомы нормированного пространства выполнены.

Если положить , то из равенства получим формально . В связи с этим возникает вопрос: нельзя ли каким-то разумным способом определить пространство , сопряженное к пространству ? Отметим кратко, что в качестве пространства принято понимать множество функций, принадлежащих одновременно всем классам .

Норма в определяется как

где - "существенная верхняя грань", т.е. наименьшее из чисел M таких, что почти всюду (т.е. всюду, за исключением, возможно, множества нулевой меры).

Можно показать, что введенное таким образом пространство является линейным нормированным пространством. В частности, неравенство Гельдера остается справедливым и при , а неравенство Минковского - при .

Отметим также, что любая непрерывная на отрезке функция (именно на отрезке, а не на интервале !) заведомо принадлежит классу , причем .

Мы не доказали пока полноту пространств . К сожалению, доказательство этого факта достаточно сложно и далеко выходит за рамки нашего спецкурса. Поэтому отметим без доказательства (отослав наиболее дотошных читателей к учебникам по функциональному анализу), что каждое пространство (где ) - полное и, следовательно, банахово пространство.

В заключение параграфа отметим несколько интересных следствий неравенства Гельдера. Во-первых, если и (где ), то из неравенства Гельдера следует, что суммируема на данном интервале, т.е. . Во-вторых, положив в неравенстве Гельдера на (a, b), получим

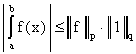
Поскольку заведомо , то получаем, что если (при ), то . Вообще, можно показать, что если и , то , т.е. пространство - подмножество ). Факты такого рода носят в математике название "теорем вложения".

ЛИТЕРАТУРА***

1. Ильин В.А., Позняк Э.Г. Основы математического анализа. Т.2. - М.: МГУ, 1973. - 448 с.

2. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. - М., 1968. - 469 с.

Исследование выполнено при поддержке Российского фонда фундаментальных исследований (Проект РФФИ №96-01-00181).

Кафедра математического анализа

Смоленского государственного педагогического университета

Поступила в редакцию 24.11.97.