УДК 519.6:519.725:681.3

ПАРАЛЛЕЛЬНАЯ ОБРАБОТКА ДАННЫХ. МЕТОДЫ И СРЕДСТВА

© В. И. Мунерман

В настоящей статье рассматриваются методы и средства параллельной обработки данных, необходимые исследователям различных специальностей для наилучшего решения задач обработки данных с помощью современных вычислительных средств. Предлагается принцип последовательно-параллельного программироввания, основанный на алгебре многомерных матриц.

ВВЕДЕНИЕ

Предлагаемая статья носит скорее научно-популярный нежели строго научный характер. Автор преследуют цель: показать широкому кругу научных работников возможности, открываемые в результате применения параллельной обработки данных.

Широкое распространение в 80-х и 90-х годах персональных компьютеров принципиально изменило не только количественный но и качественный состав пользователей вычислительной техники. Если раньше потребителями услуг компьютеров были, в основном, представители "точных" наук, то теперь компьютер становится настольным инструментом биологов, медиков, гуманитариев. При всей очевидной полезности происходящего процесса компьютеризации научных дисциплин, нельзя не заметить сопутствующую ему опасность распространения весьма вредного суеверия. Это суеверие созданное поддерживаемое hacker'ами заключается в необоснованной уверенности в том, что любая задача может быть решена на компьютере вне зависимости от ее математической модели. Если же производительности компьютера недостаточно, то следует всего лишь сделать соответствующий upgrade или сменить компьютер. Представители наук, давно использующих компьютерную обработку данных, как правило, заражены этим суеверием в гораздо меньшей степени, чем неофиты, приобщившиеся к вычислительной технике за последние полтора десятилетия. Физики, астрономы, метеорологи и многие другие наряду с персональными компьютерами широко используют современные суперкомпьютеры. Этому способствует традиция тщательного построения и проработки математических моделей исследуемых процессов. Эти модели, как правило, автоматически приводят к осознанию необходимости параллельной обработки данных.

ПАРАЛЛЕЛЬНАЯ ОБРАБОТКА ДАННЫХ И СУПЕРКОМПЬЮТЕРЫ

Идея параллельной обработки данных родилась достаточно давно. Одна из первых ее реализаций, выполненная в 40-х годах на счетно-перфорационных машинах, принадлежит выдающемуся американскому физику Р.Фейнману. Сам он по этому поводу пишет следующее.

"В итоге если раньше потребовалось девять месяцев на три задачи, то теперь мы пропустили девять задач за три месяца, что почти в десять раз быстрее. Одна из тайных уловок при решении задач была вот какой. Задачи содержались в колоде карточек, которые должны были пройти по циклу. Сначала сложи, потом умножь - так это и шло по циклу машин в комнате, медленно двигалось по кругу. Мы придумали параллельно, но в другой фазе, запустить по циклу набор карточек другого цвета. Мы делали бы две или три задачи одновременно."

Таким образом группа молодых американских физиков предложила использовать для обработки данных конвейер: что существенно повысило скорость выполнения вычислительных операций. Сегодня конвейер широко используется в вычислительной технике. Все современные процессоры выполняют команды, считывая их из оперативной памяти последовательно фрагмент за фрагментом в регистры и обрабатывая каждый фрагмент одновременно со считыванием следующего.

В качестве примера конвейерных вычислений рассмотрим вычисление функции на массиве данных X, содержащем шесть элементов. Результаты помещаются в шестиэлементный массив Y. Для вычислений можно использовать систему, состоящую из трех, не обязательно различных процессоров. Первый процессор выполняет программу, которая извлекает значение очередного элемента массива X из оперативной памяти и вычисляет значение функции . Затем результат вычислений r₁ передается второму процессору, выполняющему программу вычисления значения функции и передающему это значение третьему процессору. Третий процессор выполняет программу, вычисляющую значение , и помещает его в оперативную память. Этот процесс показан на рис. 1.

Рис. 1. Конвейерные вычисления функции

Более подробно состояния нашей трехпроцессорной системы на каждом шаге вычисления значений функции заданной на значениях массива X показаны в таблице 1.

Таблица 1

Пошаговое вычисление функции

В таблице мы видим, что на первом шаге процессор SIN занят вычислением значения . В этот момент состояния двух других процессоров и значения элементов массив Y еще не определены, что обозначено символом . На втором шаге уже заняты два процессора SIN и LN, вычисляющие, соответственно, и . Состояние процессора SQR по-прежнему не определено. Шаги с третьего по шестой соответствуют максимальной загрузке системы. Все три процессора заняты вычислениями. При этом процессор SIN извлекает из массива X очередное значение аргумента x_i и начинает вычисление значения функции от , процессор LN продолжает вычисление значения функции от , а процессор SQR завершает вычисление значение функции от и помещает его в массив Y. Последние два шага завершают вычисления, постепенно освобождая процессоры.

Второй пример продемонстрирует другой способ параллельных вычислений, основанный на одновременном выполнении несколькими процессорами одной и той же команды, но на различных данных. Пусть даны два одномерных массива A и B, из шести элементов каждый. Результат вычислений - массив C, каждый элемент которого вычисляется по формуле . Для решения этой задачи можно использовать шестипроцессорную вычислительную систему, показанную на рис. 2.

Рис. 2. Поэлементное суммирование массивов

В этом случае каждый процессор выполняет одну и ту же команду , где i - номер процессора.

Приведенные примеры иллюстрирует два базовых метода организации параллельных вычислительных систем. Эти методы соединяются во всех современных параллельных вычислительных системах - суперкомпьютерах, образуя в результате некоторую среду для решения сложных задач. Нет смысла подробно рассматривать архитектуры современных суперкомпьютеров, читатель, при необходимости, может самостоятельно ознакомиться с ними по обширной литературе [1]. Сейчас же мы приступим к рассмотрению проблем алгоритмизации и программирования задач для решения их на суперкомпьютерах.

МАТРИЧНЫЙ ПОДХОД К ПАРАЛЛЕЛЬНОЙ ОБРАБОТКЕ ДАННЫХ

Матрицы издавна использовались математиками для представления данных при решении различных задач. Алгебра матриц хорошо разработана и удобна для применения для нужд как "чистой" так и прикладной математики. Желающих подробно ознакомиться с классической теорией матриц мы отсылаем к книге [2]. В статье мы коснемся только основных аспектов алгебры матриц.

Матрицей называют прямоугольную таблицу чисел вида

.

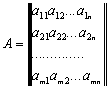
Часто используется сокращенное обозначение матрицы (i=1,2,...,m; j=1,2,...,n). Для числовых матриц легко определяются привычные алгебраические операции сложения и умножения.

Суммой двух матриц и (i=1,2,...,m; j=1,2,...n) называется матрица , элементы которой вычисляются по формуле .

Произведением двух матриц и называется матрица (i=1,2,...,m; j=1,2,...,n; j=1,2,...,n; k=1,2,...,p), элементы которой вычисляются по формуле . Например,

=

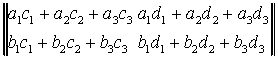
Важную роль в алгебре матриц играет операция транспонирования. В результате транспонирования матрица (i=1,2,...,m; j=1,2,...n) преобразуется в матрицу , элементы которой определяются по формуле =.

Числовые матрицы и их использование при решении различных математических и прикладных задач хорошо изучены. Известны интересные алгоритмы решения многих численных задач с помощью матриц. Однако важнейшей для нас особенностью матриц является естественный параллелизм выполнения операций над ними. Действительно, когда мы записываем сумму двух матриц A+B то подразумеваем, что все сложения выполняются одновременно. Для реализации операций над матрицами мы можем использовать систему из mn процессоров, имеющих одновременный доступ к общей оперативной памяти, в которой расположены матрицы A и B. На рис. 3 приведен пример такой системы при m=n=4, состоящей из 16 процессоров. Вычислительные системы подобные этой принято называть матричными.

Рис. 3. Вычислительная система из 44 процессоров

Если каждому процессору, находящемуся на i-той горизонтали и j-той вертикали, подать команду сложения с теми же i и j, то одновременно складывая элементы матриц, эти процессоры за одну операцию сложат две матрицы. Операция умножения матриц также может быть выполнена на этой вычислительной системе, однако при этом время выполнения будет несколько большим, так как суммирование произведений пар элементов исходных матриц потребует дополнительных затрат. При этом связь каждого процессора со своими соседями обеспечивает применение конвейерного принципа обработки данных.

МАТРИЧНЫЕ МОДЕЛИ ДЛЯ РЕШЕНИЯ ПРИКЛАДНЫХ ЗАДАЧ

В качестве примера использования матриц мы рассмотрим некоторые задачи на графах. Графы, благодаря своей наглядности и наличию многих полезных свойств, весьма популярны при решении задач в различных научных и практических областях. Читателям, незнакомым с теорией графов, рекомендуется обратиться к книге [3]. Мы определим графы как объекты, которые можно изобразить на бумаге в виде поименованных или пронумерованных точек (вершин), соединенных линиями (ребрами). Простейший и известный всем пример графа - это схема метро, на которой вершины - станции, а ребра - линии их соединяющие. Если ребра графа снабжены стрелками, указывающими из какой вершины ребро выходит и в какую входит, граф называется ориентированным. В противном случае граф называется неориентированным. На рис. 4 изображены неориентированный (a) и ориентированный (b) графы.

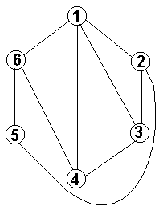
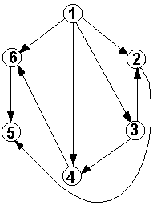
a)                                b)

Рис. 4. Графы: a) неориентированный; b) ориентированный

Естественным представлением графа является матрица связности. Если граф содержит n вершин, то его представляет матрица связности (i=1,2,...,n; j=1,2,...n). Элемент , если есть ребро ведущее из вершины i в вершину j, и равен 0 в противном случае. Так неориентированному графу (рис. 4-а) соответствует матрица связности

,

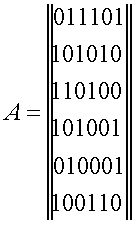
а ориентированному графу (рис. 4-b) соответствует матрица связности

.

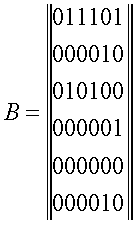
Заметим, в матрице A элементы расположены симметрично относительно главной диагонали, то есть диагонали, на которой элементы имеют индексы 11, 22, ..., 66.

Графы можно интерпретировать, например, как схемы районов города, в которых на изображены улицы с двухсторонним движением (неориентиро-ванный граф) и с односторонним движением (ориентированный граф). Эта интерпретация широко используется в практике оптимизации транспортных потоков.

Теперь после определения графа мы можем приступить к рассмотрению примеров решения задач с помощью матриц.

Пример 1. Рассмотрим ориентированный граф, изображенный на рис. 6-b. Рисунок и матрица связности показывают нам, что из вершины 1 непосредственно доступны вершины 2,3,4,6, то есть существует ребро, соединяющее вершину 1 с этими вершинами. В таком случае мы говорим что существует путь длины один из вершины 1 в вершину 2, из вершины 1 в вершину 3 и так далее. Легко заметить, глядя на рисунок, что из вершины 1 в вершину 2 можно перейти по двум ребрам через вершину 3, а в вершину 6 - по трем ребрам через вершины 3 и 4. То есть из вершины 1 в вершину 2 существует путь длины два, а в вершину 6 - путь длины три. Мы говорим, что вершина i доступна из вершины j, если существует по крайней мере один путь из вершины i в вершину j. Матрица связности отражает доступность вершин посредством путей длины один. Поставим перед собой задачу - на основе матрицы связности получить матрицы доступности вершин посредством путей длины два три и так далее.

Для решения этой задачи мы воспользуемся тем, что элементы матриц принимают только два значения 0 и 1. Следовательно мы можем использовать вместо арифметических операций сложения и умножения элементов матриц логические операции дизъюнкции V и конъюнкции . Тогда элементы суммы двух матриц вычисляются по формуле , а элементы произведения - по формуле . Рассмотрим матрицу B связности ориентированного графа (рис. 4-b). Вычислим матрицу . Она имеет вид

 .

Эта матрица отражает доступность вершин посредством путей длины два. Действительно, на ориентированном графе (рис. 4-b) существуют пути длины два из вершины 1 в вершины 2,4,5 и 6, из вершины 2 в вершины 5 и 6, из вершины 4 в вершину 5. Вычислим теперь матрицу . Ее значение

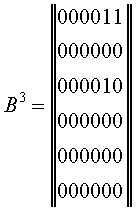
свидетельствует, что на нашем графе существуют пути длины три из вершины 1 в вершины 5 и 6, из вершины 3 в вершину 5. Заметим, что все элементы матрицы равны нулю. Это свидетельствует об отсутствии на графе путей длины четыре и больше.

Пример 2. В этом примере мы сопоставим каждому ребру ориентированного графа неотрицательное число, называемое стоимостью. Обозначим стоимость ребра ведущего из вершины i в вершину j. Пример такого графа приведен на рис. 5.

Рис. 5. Ориентированный граф с заданными стоимостями ребер

Поставим перед собой задачу для каждой пары вершин найти путь, состоящий из ребер, суммарная стоимость которых будет минимальной. Действительно, на рис. 5 мы видим, что из вершины 1 в вершину 6 ведут три пути: путь длины один, стоимость которого 8, путь длины два, через вершину 4, стоимость которого 7, и путь длины три через вершины 3 и 4, стоимость которого 6. Последний путь и будет решением задачи для вершин 1 и 6.

Для решения задачи поиска пути минимально стоимости, называемой также задачей поиска кратчайшего пути, представим граф с помощью матрицы стоимости, которую обозначим . Если нет ребра ведущего из вершины i в вершину j мы будем считать, стоимость , бесконечно большой. Тогда графу, приведенному на рис. 5, соответствует матрица

.

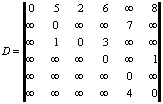
Определим операцию умножения матриц стоимости. Если A и B две матрицы, то элементы их произведения - матрицы С, вычисляются по формуле , причем сумма любого числа и равна . Вычислим матрицу

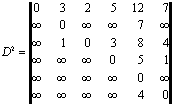
и матрицу

.

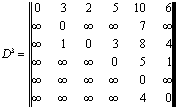
Мы видим, что элементы этих матриц отражают стоимости путей различной длины. Поскольку на нашем графе нет путей длины большей чем три, дальнейшие степени матрицы D ничем не будут отличаться от матрицы .

РАЗВИТИЕ МАТРИЧНЫХ МОДЕЛЕЙ

В предыдущем разделе мы рассмотрели применение матриц для решения задач на графах. Приведенные примеры показали, что матрицы могут базироваться на различных множествах элементов. Для того, чтобы элементы некоторого множества S могли быть элементами матрицы требуется только одно - наличие двух бинарных операций, замкнутых на этом множестве: аддитивной (+) и мультипликативной (x). Замкнутость операций означает, что если aS и bS, то a+bS и axbS. Выбор аддитивной и мультипликативной операций может быть и достаточно традиционным, как в примере 1, и весьма экзотическим как в примере 2.

Мы рассмотрели плоские матрицы, элементы которых можно трактовать как значения параметров неких реальных объектов, расположенных на плоскости в точках с целочисленными координатами. Однако на практике мы часто встречаемся с объектами, характеризующимися большим числом целочисленных координат. Такие объекты можно рассматривать как точки пространства произвольного числа измерений.

Пример 3. Рассмотрим представление информации о расходе топлива автомобилями в зависимости от марки, объема двигателя и возраста. Пусть имеются три марки автомобилей, которые мы пронумеруем от 1 до 3, два объема двигателя: 1 и 2, и возраста: 1, 2, 3, и 4 года. Тогда данные о расходе топлива можно расположить внутри трехмерного параллелепипеда (рис. 6), изобразив их точками в узлах решетки. На рисунке видно, что у всех точек целочисленные координаты.

Рис. 6. Трехмерное представление данных

Обозначим i - объем двигателя (i=1,2), j - марку автомобиля (j=1,2,3), k - возраст (k=1,2,3,4) и - значение расхода топлива, то наши данные можно представить в виде трехмерной матрицы

В общем виде определим p-мерную матрицу как совокупность элементов где индексы принимают значения от 1 до соответственно [4]. Таким образом, p-мерная матрица содержит элементов. Обозначим многомерную матрицу . Для многомерных матриц определяются операции сложения и умножения.

1) Суммой двух p-мерных матриц и с одинаковыми наборами индексов называется p-мерная матрица с тем же набором индексов, элементы которой вычисляются по формуле .

Прежде чем определить умножение многомерных матриц, рассмотрим пример умножения двух трехмерных матриц.

Пример 4. Пусть дан набор индексов i, j, k, l, размерности которых соответственно. Определим трехмерные матрицы и . Тогда:

- четырехмерная матрица , элементы которой вычисляются по формуле для всех совпадающих значений индексов j и k;

- трехмерная матрица , элементы которой вычисляются по формуле ;

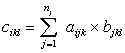
- двумерная матрица , элементы которой вычисляются по формуле

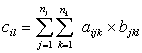
рассматриваются как различные формы произведения матриц A и B.

Определим умножение многомерных матриц в общем виде. Пусть даны две матрицы и , p и q-мерные соответственно.

Разобьем совокупности индексов и на четыре группы, содержащие соответственно , , и индексов (,,,0). Причем ++=p, а ++=q. Обозначим группы индексов как , , и . Представим матрицы A и B в виде и . Индексы групп s и c в матрицах A и B полностью совпадают. Тогда матрица , элементы которой вычисляются по формуле , называется произведением матриц A и B. Алгоритм реализации этой операции весьма прост: сначала перемножаются все пары элементов, у которых полностью совпадают значения индексов групп s и c, а затем суммируются все произведения с одинаковыми значениями индексов группы c. Произведение многомерных матриц называется (свернутым произведением и обозначается . 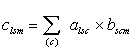Из определения (свернутого произведения следует, и пример 4 это подтверждает, что для любой пары многомерных матриц можно, подбирая различные значения и , построить много различных произведений.

Многомерные матрицы являются мощным аппаратом математического моделирования для различных предметных областей. Например, автор использовал их для построения модели оптимизации процессов обработки данных на суперкомпьютерах [5].

МНОГОМЕРНЫЕ МАТРИЦЫ И ТЕХНОЛОГИИ ПРОГРАММИРОВАНИЯ

Обработка многомерных матриц хорошо согласуется с современными принципами разработки программного обеспечения, в частности с объектно-ори-ентированным программированием.

Рассмотрим совокупность типов данных, , для каждого из которых определены аддитивная и мультипликативная операции. Тогда кортеж , где (i=1,...,n), можно рассматривать как объект наследующий все свойства типов , в том числе и операции сложения и умножения элементов кортежей. Для кортежей также можно определить аддитивную и мультипликативную операции. Это может быть поэлементное сложение и умножение. Такой подход позволяет нам определить многомерную матрицу кортежей как объект, наследующий свойства объекта-кортежа. Построение многомерной матрицы кортежей показано на рис. 7. Мы используем здесь принцип множественного наследования. Направление наследования свойств на рисунке - сверху вниз.

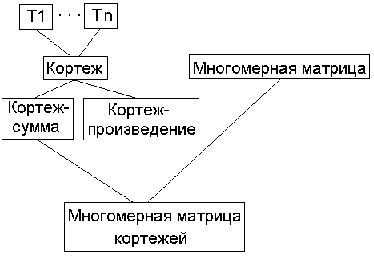
Рис. 7. Объектная модель многомерной матрицы кортежей

Рассмотренные нами свойства многомерных матриц позволяют в заключение сформулировать один принцип, который позволяет облегчить алгоритмизацию задач, для решения которых необходимо использование суперкомпьютеров.

ПРИНЦИП ПОСЛЕДОВАТЕЛЬНО-ПАРАЛЛЕЛЬНОГО ПРОГРАММИРОВНИЯ

Сформулируем принцип последовательно-параллельного программирования в виде следующих четырех положений:

- в качестве базового типа данных используется алгебра многомерных матриц;

- операции этой алгебры реализуются как базовые процедуры обработки данных для конкретных суперкомпьютеров, с максимально допустимой степенью параллелизма;

- многомерные матрицы включаются в языки программирования как самостоятельные объекты;

- алгоритмы представляются как последовательности операций над многомерными матрицами.

Перечислим основные достоинства принципа последовательно-па-раллельного программирования.

Во-первых, исключается связь между свойствами конкретной архитектуры суперкомпьютера и способностью данного алгоритма к распараллеливанию.

Во-вторых, ограничивается число реализуемых параллельно алгоритмов так как необходимо распараллелить только операции алгебры многомерных матриц. Поэтому можно наиболее полно использовать возможности данного суперкомпьютера для оптимизации программ, реализующих эти операции.

В-третьих, алгоритм и программа, реализующие задачу из некоторой предметной области разрабатываются как обычные последовательные алгоритмы и программы. Данные, представленные в виде многомерных матриц, последовательно обрабатываются операциями алгебры многомерных матриц как неделимые объекты. Такой подход наиболее естественен для человека.

В-четвертых, программа выполняется на суперкомпьютере параллельно, так как каждая операция над многомерными матрицами реализуется параллельным алгоритмом.

ЗАКЛЮЧЕНИЕ

Параллельная обработка данных превращается сегодня из экзотики компьютерного мира в естественный и необходимый при решении подавляющего большинства задач метод обработки данных. Рассмотренный в этой статье метод, основанный на работе с многомерными матрицами, позволяет исследователям в различных областях науки разрабатывать модели, которые без труда можно будет реализовать на суперкомпьютерах.

Например, анализ задачи оценки виброзащитных характеристик, при обработке результатов летных испытаний показал, что исходные данные удобно представляются с помощью многомерных матриц, а алгоритмы сводятся к выполнению операций над этими матрицами. Применение принципа последовательно-параллельного программирования при решении этой задачи позволил существенно повысить эффективность этих алгоритмов благодаря параллельной реализации на суперкомпьютерах [6].

Одним из направлений использования метода последовательно-параллельного программирования являются экспертные системы. Многомерные матрицы представляют собой идеальное средство для классификации и представления правил принятия решений.

Сказанное позволяет надеяться, что применение изложенного в статье метода обеспечит многим научным работникам возможность решения сложных задач, требующих больших объемов вычислений.

ЛИТЕРАТУРА

1. Головкин Б.А. Вычислительные машины с большим числом процессоров. - М.:Радио и связь, 1995.
2. Гантмахер Ф.Р. Теория матриц. - М.:Наука, 1967.
3. Оре О. Теория графов. - М.:Наука, 1968.
4. Соколов Н.П. Введение в теорию многомерных матриц. - Киев: Наукова думка, 1972.
5. Гендель Е.Г., Мунерман В.И. Применение алгебраических моделей для синтеза процессов обработки файлов. - УСиМ. - 1984. - № 4. - С. 69-72.
6. Митенков В.Б., Конычев В.И., Емельченко Е.П., Муннерман В.И., Самойлов М.Ю., Самойлова Т.А. Эффективное решение задач обработки результатов летных испытаний на суперкомпьютерах. // Тезисы докладов к международной конференции "Авиационные технологии 2000". - Жуковский, 1997. - С. III-16.

Кафедра информатики

Смоленский государственный педагогический университет

Поступила в редакцию 13.12.97.