УДК: 519.6 : 519.725
На примере широко известного метода кодирования, основанного на построении дерева Хаффмена, рассмотрена возможность параллельных вычислений с использованием матричного представления данных и специально определяемой операции матричного умножения над ними. Получены временные оценки наиболее трудоемких по вычислительной сложности этапов кодирования при их реализации на суперкомпьютерах.
Введение
Метод сжатия информации на основе двоичных
кодирующих деревьев был предложен Д. А. Хаффменом
в 1952 году[1] задолго до появления современного
цифрового компьютера. Обладая высокой
эффективностью, он и его многочисленные
адаптивные версии[2] лидируют среди методов,
используемых в алгоритмах кодирования. Однако
при обработке информции в режиме реального
времени[3] большая вычислительная сложность
метода ограничивает его использование, а с
ростом объемов кодируемой информации требуемые
временные характеристики может обеспечить
только параллельная обработка данных на
суперкомпьютерах[4,5,6,7]. В работе [8] рассмотрена
возможность параллельной реализации алгоритма
JPEG упаковки графической информации с
использованием классических операций матричной
алгебры для первых двух этапов сжатия:
построение матрицы дискретного косинусного
преобразования и округления матрицы частотных
коэффициентов. Распараллеливание последнего
достаточно трудоемкого этапа сжатия, в котором
строится дерево Хаффмена, не проводилось, ввиду
явно последовательного характера построения
дерева. В настоящей работе предлагается
параллельная реализация этого этапа, основанная
на расширении операций матричной алгебры.
Ожидаемая оценка производительности
параллельных вычислений проводится по значению
ускорения S , которое определяется следующим
образом: S = T(1)/T(p), где T(1) - время реализации
алгоритма на одном процессоре, T(p) - время
реализации алгоритма на p параллельных
процессорах.
Оценка сложности последовательного
алгоритма
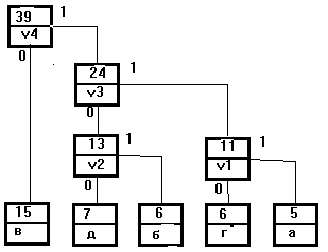
Идея хаффменовского сжатия набора символов, составляющих сообщение, состоит в следующем: символам, встречающимся в сообщении с большей вероятностью, присваиваются более короткие коды. Получаемые коды имеют уникальный префикс, что позволяет однозначно их декодировать, несмотря на их переменную длину. Алгоритм построения H-дерева , на котором основано кодирование, прост и элегантен.
1.Символы входного алфавита образуют список из N свободных узлов. Вес узла равен либо вероятности, либо количеству вхождений элемента алфавита в сжимаемое сообщение.
2. Выбираются два свободных узла дерева с наименьшими весами.
3. Создается их родитель с весом, равным их суммарнрму весу.
4. Родитель добавляется в список свободных узлов, а двое его детей удаляются из этого списка.
5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1 , а другой - бит 0.
6. Шаги, начиная со второго, повторяются до тех
пор, пока в списке свободных узлов не останется
только один свободный узел. Он и будет считаться
корнем дерева.
При количестве символов алфавита N число
повторений п.2,3,4,5 равно N-1. Допустим, у нас
есть следующее множество элементов входного
алфавита(N=5) и соответствующие им веса:
а б в г д
5 6 15 6 7
Построенное по данному множеству дерево
кодирования Хаффмена, содержащее четыре новых
последовательно добавляемых узла-родителя v1,v2,v3,v4,
представлено на рисунке 1. Коды образуются по
пути движения от корня дерева вниз к узлам.
|
вес | код |
| в | 15 | 0 |
| д | 7 | 110 |
| б | 6 | 101 |
| г | 6 | 110 |
| а | 5 | 111 |
Рис. 1. Дерево кодирования Хаффмена и
сответствующие ему коды
Оценим временную сложность T(1),T(2),T(3) трех шагов последовательного алгоритма кодирования: определения весов дерева по исходному сообщению, выбора двух минимальных весов, замены исходных символов кодами. Пусть M - число символов в сообщении, кодируемых по Хаффмену и принадлежащих исходному алфавиту из N элементов. (Некоторые из символв сообщения могут кодироваться с использованием других методов, например, с помощью алгоритма кодирования повторов RLE.) Для определение частоты встречаемости символов необходим один проход по сообщению, следовательно, сложность вычисления весов исходных узлов дерева при реализации алгоритма на однопроцессорном компьютере составит T1(1)=O(M). Временная сложность этапа построения дерева T2(1) может быть вычислена как произведение числа добавляемых родительских вершин на сложность выбора двух минимальных весов, определяемую максимальным числом сравнений с неудаленными элементами алфавита, равным 1+2+3+.....+N = N*(N+1)/2. Полагая N>>1, получим T2(1)=O(N3/2). Еще один проход по сообщению потребуется для замены M символов на их H-коды со сложностью T3(1)=O(M). При использовании дерева в улучшенных по быстродействию адаптивных версиях кодирования этап замены символов объединяется с этапом построения дерева, так что для этих версий можно полагать T3(1)=0.
Таким образом общее время построения дерева и
собственно кодирования даже для улучшенных
адаптивных версий будет не менее
T(1)=T1(1)+T2(1)+T3(1) = M+N3/2 (1)
Для возможности использования параллельных матричных операций представим алгоритм построения H - дерева в следующей форме:
Определить частоты встречаемости символов в сообщении, составляющих его алфавит. N ненулевых элементов алфавита - исходное множество узлов дерева.
Пока число новых узлов меньше N-1
Упорядочить узлы.
Добавить новый узел, соответствующий двум минимальным.
Для всех символов алфавита добавить очередной разряд в код Хаффмена.
Конец Пока
Заменить символы на их коды.
Рассмотрим особенности матричных операций при
реализации каждого из этапов данного алгоритма.
Матричные операции
Векторно-матричные операции произвольной размерности n могут считаться базовыми для современных суперкомпьютеров. Это операции сложения, умножения, транспонирование и свертки матриц[5 ]. Однако для нашей невычислительной задачи, имеющей комбинаторный характер, мы не можем ограничиться рассматрением матриц, определенных только над полем вещественных чисел. Нам необходимо определить операции над элементами матриц таким образом, чтобы результат их сложения или умножения мог отличаться от традиционных суммы и произведения. Аналогичный подход был предложен в [6] для описания последовательных комбинаторных алгоритмов.
Рассмотрим множество, состоящее из элементов , где символ
обозначает неопределенное
значение. Пусть T- множество, которому
принадлежат элементы матрицы, и P, P1, P2 -
предикаты, определенные на T. Тогда операци
и
для любых
определим как
=
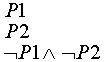
=
.
(3)
Элементы Cij матрицы C = AB будем вычислять по
формулам
(4)
или
, (4')
в зависимости от реализуемого алгоритма.
Согласно[7], степень параллелизма при
вычислении C равна числу необходимых
операций умножения ,
что для размеров исходных матриц - сомножителей L*n
и n*K составит L*K*n. Суммы членов в (4) или
(4') могут быть получены методом каскадных сумм за
время
TM = LOG2( n), (5)
которое и определит временную вычислительную сложность параллельной реализации данного умножения для L*K*n процессоров.
Определение частот встречаемости
символов в сообщении
Представим исходное сообщение, символы
которого принадлежат множеству входного
алфавита S={s1,s2,....,sN}, матрицей A размера L*K.
. Пусть X- искомый вектор из N чисел,
каждое из которых равно числу вхождений
соответствующего элемента алфавита в исходное
сообщение. Для нахождения его значений образуем
новую матрицу B размера K*N, каждая строка
которой состоит из элементов алфавита S, так что bi1=s1,
bi2=s2, ..., biN=sN. Выполним умножение
матриц AB, определив
в нем операцию умножения компонент
=
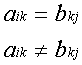
Каждая строка произведения AB будет соответствовать числу
вхождений соответствующего символа алфавита в
строку матрицы исходного сообщения A. Свертка
произведения по столбцам (сверху - вниз) позволит
получить искомый вектор X. При представлении
входной матрицы как вектора размера 1*K
свертки не потребуется. Поясним использование
данной матричной операции для определения
частот встречаемости на примерах.
Пример 1.Сообщение A представлено матрицей чисел из алфавита{1,2,3,...,9}.
A= 
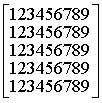
B =
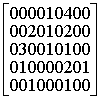
После свертки произведения сверху-вниз получим
X=,
где нулевые значения имеют элементы алфавита,
не вошедшие в сообщение.
Пример 2. Информация представлена вектором чисел A из алфавита{1,2,3,...,9}.
A = B=

B =
Пример 3.Информация представлена вектором символов A из алфавита{a,b,c,d,...,z}.
A= B=
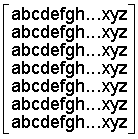
a b c d e f g h i ... z
AB =
.
Оценим временную вычислительную сложность T1(p) параллельной реализации этапа определения частоты встречаемости символов, полагая число процессоров p равным степени параллелизма операции умножения матриц. Заметим, что число сложений этапа не зависит от матричного или векторного представления исходных данных, так как и в первом случае общее число сложений с учетом свертки составит L*K=M. Тогда для M кодируемых символов время этапа согласно (5), составит
T1(p)=LOG2( M). (7)
Упорядочение узлов дерева
Рассмотрим возможность использования
введенной операции матричного умножения для
упорядочения элементов, составляющих вектор
исходных значений A длины N. Назовем
вектором упорядоченности C
последовательность индексов, соответствующую
расположению элементов A в порядке их
возрастания. Для нахождения значений этого
индексного вектора упорядоченности образуем
новую матрицу B размера N*N, каждая строка
которой состоит из элементов исходного вектора A.
Выполним умножение матриц AB, определив в нем только операцию
умножения компонент
aikbkj
=
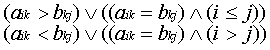
Чтобы получить индексный вектор
упорядоченности
C=
выполним умножение исходного вектора A на матрицу B , c учетом (8) и при арифметическом сложении:
C = AB ,
где B=
. (9)
Проиллюстрируем операцию упорядочения примером. Пусть повторяемость элементов множества { а б в г д} кодируемого сообщения задана вектором
а б в г д
A = .
Для упорядочения элементов A выполним
умножение матриц AB .
Получим вектор индексов
C=
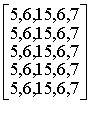
,
каждый элемент которого вычисляется с использованием отношения (8) и арифметического сложения.
Например,
C12 = 56
+ 6
6 +15
6 +6
6 +7
6 = 0+1+1+0+1 = 3.
Индексный вектор C этого примера соответствует упорядоченной последовательности расположения элементов в,д,б,г,а у основания дерева рисунка1. Два наименьших в последовательности - это элементы г, а с весами 1, 2.
Оценим вычислительную сложность этапа
упорядочения. Для набора кодируемых символов,
представленных вектором длины N, время
параллельной реализации матричного умножения T2(p)
для числа процессоров p = N2 составит
T2(p) = LOG2( N) (10)
Добавление нового узла
Для выбора двух минимальных узлов и добавления
соответствующего им нового узла-родителя
преобразуем вектор C , добавив в него
незначащие разряды для всех пока не созданных
вершин. Для приведенного выше примера
индексации, соответствующего дереву рисунка1,
преобразованный вектор C будет иметь вид:
v1 v2 v3 v4 а б в г д
C =[ _ , _ , _ , _ , 1, 3, 5, 2, 4 ].
Выполним над C две операции. Первая,
матричная, заключается в создании для каждого
нового узла вектора кода D длины 2*N-1,
разряды которого соответствуют полному
множеству как исходных, так и новых узлов дерева.
Вектор D содержит коды 1,0 в разрядах двух
минимальных вершин и код 1 в разряде новой
родительской вершины. Вторая операция состоит в
добавлении к вектору A разряда для значения
веса новой вершины, вычисления этого значения и
удаления двух минимальных значений. Для
нахождения значений D умножим вектор C на
матрицу B, значение которой формируются
разверткой C. При этом операцию умножения
определим как
cikbk
=
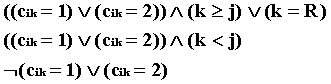
где R - номер добавляемой вершины.
Операцию сложения
определим в виде
=
(12)
Тогда вектор D кодов двух наименьших и
родительской вершин получим операцией
матричного умножения D=CB. Например, для R = 1 и C = [_,_,_,_,1,3,5,2,4]
получим
D = CB =
[1,_ ,_ ,_ ,1,_ ,_ ,0 ,_].
В таблице 1 представлены результаты выполнения
матричных операций для образования вектора
частоты встречаемости A, упорядочения C и
кодов вершин D при добавлении всех четырех
родительских узлов v1,v2,v3,v4 дерева рисунка 1.
Таблица 1
| v1 | v2 | v3 | v4 | |||||||||
| A | C | D | A | C | D | A | C | D | A | C | D | |
| v1 | 1 | 11 | 3 | 11 | 1 | 1 | ||||||
| v2 | 1 | 13 | 2 | 0 | ||||||||
| v3 | 1 | 24 | 2 | 1 | ||||||||
| v4 | 1 | |||||||||||
| а | 5 | 1 | 1 | |||||||||
| б | 6 | 3 | 6 | 1 | 1 | |||||||
| в | 15 | 5 | 15 | 4 | 15 | 3 | 15 | 1 | 0 | |||
| г | 6 | 2 | 0 | |||||||||
| д | 7 | 4 | 7 | 2 | 0 | |||||||
Оценим вычислительную сложность этапа. Для N
кодируемых символов исходного алфавита,
представленных вектором размера N, время
матричного умножения, равное общему времени
этапа, составит
T3(p) = LOG2( N). (13)
Формирование кодовых разрядов
Очередной разряд кодов Хаффмена для всех кодируемых символов можно добавить, используя операцию матричного умножения следующим образом. При добавлении очередной K-ой вершины разобьем сформированный вектор D на два: вектор Q, соответствующий элементам исходного алфавита и вектор P, состоящий из элементов родительских разрядов.
Пусть H - матрица кодов, столбцы которой - это
векторы Q, каждый из которых соёответствует
добавленной вершине. Размер матрицы кодов равен N*R,
где R- порядковый номер добавляемого узла -
родителя. Тогда R-ый вектор - столбец матрицы
кодов Хаффмена может быть получен умножением
матрицы Н на вектор P. При этом операции
умножения и сложения определим следующим
образом:
hikpk1
=
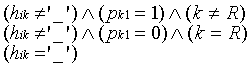
=
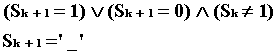
Рис. 2, 3, 4 ииллюстрируют изменения в матрице колов H при создании родительских вершин дерева рис. 1.
Только при создании первой и второй
родительских вершин v1 и v2 операция умножения HP не изменит столбец
кодов в матрице H (рис. 2). Это объясняется тем,
что что эти вершины связаны с исходными узлами
непосредственно, а не через узлы - родители.
| V 1 |
V 2 |
V 2 |
V 2 |
|||||
| а б в г д |
1 - - 0 - |
- 1 - - 0 |
V1 V2 |
- 1 |
а б в г д |
- 1 - 1 0 |
||
| * | = | |||||||
Рис.2. Формирование кодового разряда v2
матрицы кодов H путем умножения ee на вектор P
При последующих умножениях, которые
выполняются при добавлении родительских вершин v3
и v4, связанных с исходными узлами другими
“родителями”, в матрице кодов H появятся
новые разряды.
| V 1 |
V 2 |
V 3 |
V 3 |
V 3 |
|||||
| а б в г д |
1 - - 0 - |
- 1 - - 0 |
- - - - - |
V1 V2 V3 |
1 0 1 |
а б в г д |
1 0 - 1 0 |
||
| * | = | ||||||||
Рис.3. Расширение матрицы кодов H при добавлении третьей вершины
| V1 | V2 | V3 | V4 | V4 - - 1 1 |
V4 | V1 | V2 | V3 | V4 | |||||||
| а | 1 - - 0 - |
- 1 - - 0 |
1 0 - 1 0 |
- - 0 - - |
V1 V2 V3 V4 |
а б в г д |
1 1 0 1 1 |
а б в г д |
1 - - 0 - |
- 1 - - 0 |
1 0 - 1 0 |
1 1 0 1 1 |
||||
| б | * | = | ||||||||||||||
| в | ||||||||||||||||
| г | ||||||||||||||||
| д |
а)
б)
Рис. 4.
а)Формируется последний разряд кодовой матрицы
б)Матрица после добавления последней
вершины v4( коды Хаффмена расположены справа
налево)
Оценим вычислительную сложность этапа. Для N
кодируемых символов исходного алфавита время
матричного умножения составит
T4(p)= LOG2( N) (16)
Для замены символов сообщения кодами дерева из
матрицы H предполагается одновременное
параллельное вычисление суммарной длины
кодового набора, предшествующего коду каждого из
символов, составляющих сообщение.
Вычислительная сложность суммирования M
элементов при числе процессоров p=M/2 составит
T5(p)= LOG2( M). (17)
Суммарная оценка эффективности
распараллеливания
С учетом повторения этапов для каждой новой из
N-1 вершин, общее время кодирования T(p) с
использованием дерева Хаффмена составит
T1(p)+(N-1)*(T2(p)+T3(p)+T4(p))+T5(p). (18)
Подставляя в (18) выражения (7),(10),(13),(16),(17), получим
для параллельных вычислений
T(p)=2*LOG2(M)+3*LOG2(N) (19)
Ускорение вычислений S=T(1)/T(p), с учетом (1),
составит
S=(M+N3/2)/(2*LOG2(M)+3*LOG2(N)). (20)
На рис.5 представлены графики зависимостей ускорения параллельных вычислений S от длины кодируемого сообщения для входных алфавитов разной мощности N=256, 512 и 1024 .
Рис.5.Зависимость ускорения S параллельных
вычислений от длины входного
кодируемого сообщения M при
различной мощности алфавита N
Таким образом можно утверждать, что
использование предлагаемых матричных операций
позволиляет достаточно эффективно
распараллелить невычислительный комбинаторный
алгоритм кодирования, имеющий большую
вычислительную сложность и не обладающей
естественным параллелизмом . В работе показано,
что при параллельном исполнениии данного
алгоритма, основанного на построении двоичных
кодирующих деревьев Хаффмена, может быть
достигнуто многократное ускорение вычислений.
ЛИТЕРАТУРА
1. Huffman D.A. A Method for the construction of minimum - redundacy codes // IRE.-September 1952.- Vol.40.-N9. Русский перевод: Д.А.Хаффмен. Метод построения кодов с минимальной избыточностью// М.: Мир, Кибернетический сборник.- 1961.- Вып.3.
2. Мастрюков М. Алгоритмы сжатия информации. Часть 1. Сжатие по Хаффмену. // Монитор, 1993. - № 7-8. - С.14-24.
3. Поммерт А., Пфлессер Б. Визуализация объема в медицине. //Открытые системы, 1996. - № 5. - С.56-61.
4. Головкин Б. А. Вычислительные системы с большим числом процессоров. М.: Радио и связь,1995.
5. Прангишвили И.В. Виленкин С.Я. Медведев И.Л. Параллельные вычислительные системы с общим управлением. - М.: Энергоатомиздат, 1983.
6. Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. - М.: Мир, 1979.
7. Хокни Р., Джессхоуп К. Параллельные ЭВМ. - М.: Радио и связь, 1986.
8. Самойлов М.Ю.,Самойлова Т.А, Норицина И.Ю.// Математическая морфология. - 1997. - Т. 2. - Вып. 2. - С. 99-108.
Кафедра информатики
Смоленский государственный педагогический университет
Поступила в редакцию 13.12.97.