Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 10. -
Вып. 2. - 2011. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/TITL-30.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/cont.htm
УДК
621.391
ИСПОЛЬЗОВАНИЕ
МАТЕМАТИЧЕСКОЙ СИСТЕМЫ MATLAB ДЛЯ МОДЕЛИРОВАНИЯ СИСТЕМЫ
НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА
Ó 2011 г. Финогенов С. Н.
В работе
предлагается для моделирования динамических систем и устройств где необходимо составлять
и решать системы дифференциальных уравнений, чаще всего нелинейных использовать
матричную систему MATLAB и ее приложение Simulink.
Ключевые
слова: Simulink, динамические системы.
Одним из наиболее важных и
ответственных этапов в проектировании систем управления сложными объектами
является разработка модельного комплекса, под которым понимается семейство
различного класса математических моделей с той или иной степенью сложности,
предназначенных для отработки систем управления и оценки их характеристик.
Математическое моделирование
– это область науки и техники, которая обеспечивает выявление закономерностей
протекания различных явлений окружающего нас мира или работы систем и устройств
путем их математического описания и моделирования без проведения натурных
испытаний. При этом используются фундаментальные положения и законы математики,
описывающие моделируемые явления, системы или устройства на некотором уровне их
идеализации. Для моделирования динамических систем и устройств необходимо
составлять и решать системы дифференциальных уравнений, чаще всего нелинейных.
Матричная система MATLAB и ее приложение Simulink – идеальное средство для реализации
такого моделирования [1].
Рассмотрим систему самонаведения летательного аппарата [2].
Структурная исходная схема
контура самонаведения при движении ракеты в вертикальной плоскости представлена
на рис. 1.
Кроме аппаратурной части на
структурной схеме изображена структурная схема кинематического звена,
отображающая объективную связь нормальных ускорений ракеты 
и цели 
с угловой скоростью
линии визирования цели.
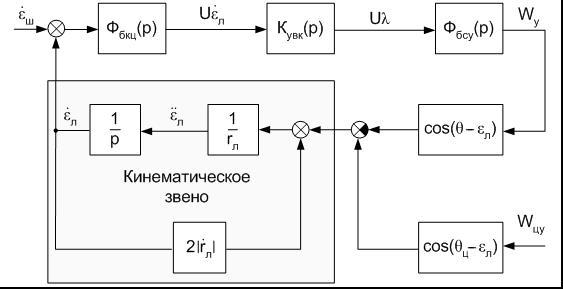
Рисунок
1 − Структурная схема контура самонаведения ракеты
Передаточная функция
аппаратурной части
с достаточной в большинстве
случаев для практики точностью может быть аппроксимирована апериодическим
звеном
,
где 
- коэффициент передачи;
- эквивалентная постоянная времени,
отображающая инерционные свойства аппаратурной части контура самонаведения.
Обычно углы упреждения 
невелики, так что
можно полагать 
, т. е. считать, что трансверсальное (перпендикулярное к линии
визирования цели) ускорение ракеты 
. Трансверсальное ускорение цели 
является внешним
воздействием на контур самонаведения и его можно заменить эквивалентным
нормальным ускорением цели 
. Тогда с учётом изложенного можно построить расчётную
структурную схему контура самонаведения (рис. 2), на которой показаны только
задающее воздействие 
, обусловленное движением цели, и возмущающее воздействие 
, обусловленное помехами и шумами на входе БКЦ (в него входят
также пересчитанные по входу БКЦ внутренние шумы бортовой радиоэлектронной
аппаратуры, флюктуации управляющих сил и т. д.).
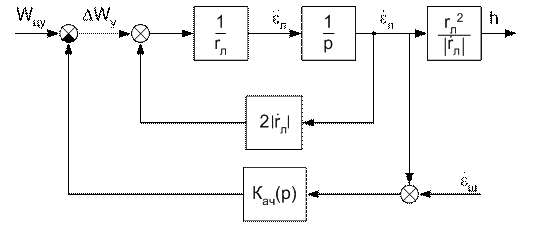
Рисунок 2 − Структурная расчётная схема
контура самонаведения ракеты
Особенности структурной
схемы контура самонаведения обусловлены свойствами КЗ и состоят в следующем:
звено
с коэффициентом передачи 
в составе КЗ делает
контур самонаведения существенно нестационарным, что создаёт трудности при
анализе его устойчивости и качества. Применение методов теории линейных стационарных
систем автоматического управления (в том числе метода логарифмических частотных
характеристик) путём «замораживания» коэффициентов даёт большие погрешности при
малых значениях 
(вблизи точки встречи),
поскольку интенсивность изменения коэффициента 
возрастает по мере
сближения ракеты с целью (
). Аналитические методы анализа, основанные на точном решении
приближенного дифференциального уравнения, описывающего динамику самонаведения,
достаточно трудоёмки и вследствие погрешностей математической модели (из-за
упрощения уравнения) также сопряжены с довольно значительными погрешностями.
Поэтому в качестве основного метода анализа динамики самонаведения
используются математическое моделирование на АВМ и ЦВМ, а также полунатурное моделирование
на специальных моделирующих стендах;
положительная
обратная связь в составе КЗ делает зенитную ракету, как объект управления,
неустойчивой, что создаёт дополнительные трудности при формировании команд
управления полётом, т. е. при построении УВК.
Для построения
функциональной блок-схемы моделируемых устройств Simulink имеет обширную библиотеку
блочных компонентов и удобный редактор блок схем [3]. Он основан на графическом
интерфейсе пользователя и по существу является типичным средством
визуально-ориентированного программирования. Создание блок схемы системы или
устройства (модели) происходит следующим образом: используя палитры компонентов
(наборы), с помощью мыши нужные блоки с палитр переносятся на рабочий стол пакета
Simulink и соединяются линиями входы и выходы блоков.
Библиотека блочных
компонентов включает источники сигналов с практически любыми временными
зависимостями, масштабирующие, линейные и нелинейные преобразователи с
разнообразными формами передаточных характеристик, квантующее устройство,
интегрирующие и дифференцирующие блок и т. д. В библиотеке имеется целый набор
виртуальных регистрирующих устройств – от простых измерителей типа вольтметра
или амперметра до универсальных осциллографов, позволяющих просматривать временные
зависимости выходных параметров моделируемых систем.
Запуск модели происходит
нажатием кнопки «Start Simulation» на панели инструментов
окна Simulink. Просмотр графиков исследуемых сигналов
осуществляется путем двойного нажатия правой кнопки мыши на блоке Scope.
В результате создания модели
контура самонаведения ЗУР на рабочем столе пакета Simulink образовалась схема (рис. 3)
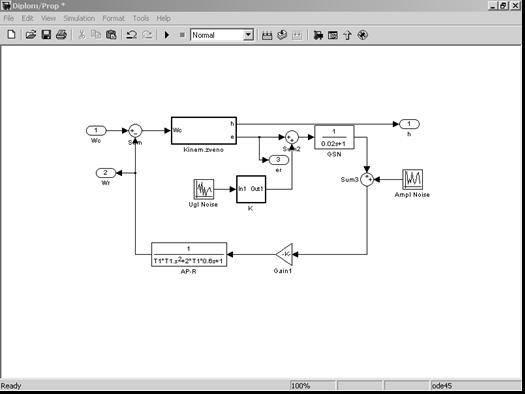
Рисунок 3 − Модель
системы самонаведения ЗУР
Результаты моделирования
отображаются в виде, показанном на рис. 4.
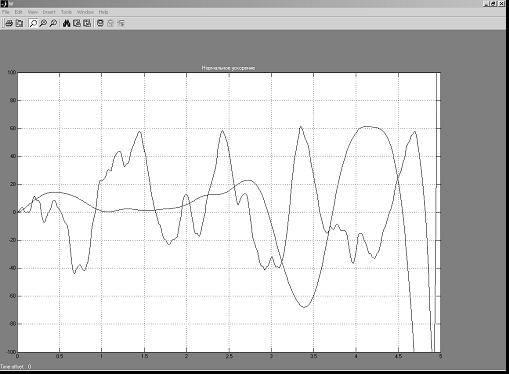
Рисунок 4 −
Зависимость нормального ускорения ракеты от времени наведения
Таким образом, MATLAB,
будучи мощной матричной системой, открывает обширные возможности в выполнении
численного моделирования как линейных, так и нелинейных систем и устройств,
описываемых большими системами уравнений. Такое моделирование предполагает
решение системы уравнений состояния достаточно апробированными и хорошо известными
численными методами – в том числе на основе рекуррентных и итерационных
алгоритмов.
В состав системы MATLAB
входит пакет моделирования динамических систем – Simulink. Уже в силу своего названия
Simulink выполняет как бы симуляцию работы моделируемых
систем и устройств. В науке это принято называть имитационным моделированием.
Пакет Simulink
– является ядром интерактивного программного комплекса, предназначенного для
математического моделирования линейных и нелинейных динамических систем и
устройств, представленных своей функциональной блок-схемой (моделью).
Литература
1. Дьяконов В. П. Matlab
6/ 6.1/ 6.5. Simulink 4/ 5. Основы применения. М.: СОЛОН-Пресс, 2004.
2. Хуторской И. Н. Теория
стрельбы ЗУР. Основы теории полета и управления зенитными ракетами. Смоленск:
ВУ войсковой ПВО ВС РФ, 2000.
3. Черных И. В. Simulink
среда создания инженерных приложений. М.: ДИАЛОГ-МИФИ, 2004.
USE
OF MATHEMATICAL SYSTEM MATLAB FOR MODELLING OF SYSTEM OF PROMPTING OF THE
FLYING MACHINE
Finogenov
S. N.
In work it is offered for modeling of dynamic systems
and devices where it is necessary to make and solve systems of the differential
equations, more often nonlinear to use matrix system MATLAB and its appendix
Simulink.
Key words: Simulink, dynamic systems.
Академия войсковой ПВО Вооруженных Сил РФ
им. Маршала Советского
Союза А. М. Василевского, г. Смоленск
Поступила в редакцию 30.03.11.