Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 10. -
Вып. 2. - 2011. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/TITL-30.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/cont.htm
УДК 517.927
Обобщенная краевая задача Валле-Пуссена для сильно-сингулярных
дифференциальных уравнений высших порядков
Ó
2011 г. Исраилов С. В., Сагитов А. А., Юшаев С. С.
В статье
рассматривается новый класс сильносингулярных дифференциальных уравнений высших
порядков специальной конструкции и доказывается теорема существования решения
обобщенной краевой задачи
Валле-Пуссена.
Ключевые
слова: сингулярность, сильная сингулярность, задача
Валле-Пуссена, теорема о существовании решения.
В [1] говорилось о существовании
сильно-сингулярных дифференциальных уравнений высших порядков, производные
решений которых до определенного порядка в точках сингулярностей могут иметь
неограниченные разрывы. Например, дифференциальное уравнение
![]() ,
,
имеет
точку сингулярности ![]() и общее решение
и общее решение
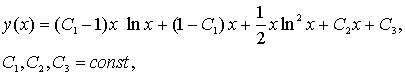
непрерывное
на сегменте [0,1]. Однако, его производные
![]()
для любых значений ![]() при
при ![]() обращаются в
бесконечность. То же самое в отношении уравнения
обращаются в
бесконечность. То же самое в отношении уравнения
![]() ,
,
с
общим решением
![]()
и
его производными
![]() .
.
Все это
связанно с присутствием в данных дифференциальных уравнениях неинтегрируемых в
несобственном смысле на сегменте [0,1] функций ![]() , как объектов сильной сингулярности. В этих примерах на левом конце [0,1] нельзя
задавать граничные условия с участием производных
, как объектов сильной сингулярности. В этих примерах на левом конце [0,1] нельзя
задавать граничные условия с участием производных ![]() в отличии от
сингулярных уравнений [2], имеющих слабые сингулярности.
в отличии от
сингулярных уравнений [2], имеющих слабые сингулярности.
Как мы
заметили, после каждого интегрирования в неопределенном смысле функций, являющихся
носителями сильной сингулярности, их дифференциальные свойства в окрестности
особой (сингулярной) точки улучшаются и через определенное количество шагов
производные низших порядков и само решение уравнения становятся непрерывными
функциями. Этот факт нами будет использован с целью ослабления влияния точек
сингулярностей функций, присутствующих в правых частях сильно-сингулярных
дифференциальных уравнений.
Класс
дифференциальных уравнений высших порядков, имеющих решения с разрывными до
определенных порядков в точках сингулярностей производными будем записывать в
квазилинейном виде
![]() , (1)
, (1)
где функции ![]() непрерывны в области
непрерывны в области ![]() по совокупности
аргументов, а концы сегмента
по совокупности
аргументов, а концы сегмента ![]() являются точками
сингулярностей для них, порождающими бесконечные разрывы у производных
являются точками
сингулярностей для них, порождающими бесконечные разрывы у производных ![]() любого непрерывного
решения
любого непрерывного
решения ![]() с непрерывными на
с непрерывными на ![]() производными
производными ![]() .
.
Пусть ![]() некоторая
фиксированная точка на интервале
некоторая
фиксированная точка на интервале ![]() . Тогда путем формального интегрирования дифференциального
уравнения (1) получим
. Тогда путем формального интегрирования дифференциального
уравнения (1) получим
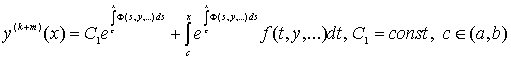 . (2)
. (2)
Производная ![]() выше
выше ![]() го порядка решения
го порядка решения ![]() внутри
внутри ![]() будет непрерывной и
можно положить
будет непрерывной и
можно положить ![]() данное число. Из (2) после
данное число. Из (2) после ![]() кратного интегрирования в неопределенном смысле имеем
кратного интегрирования в неопределенном смысле имеем
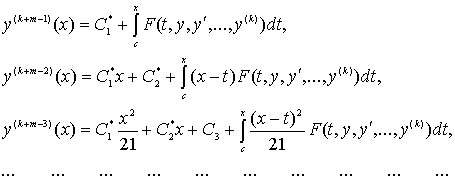 (3)
(3)
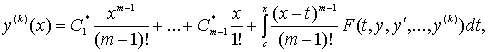
где
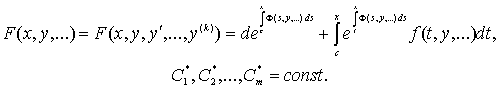 (4)
(4)
В дальнейшем будут использованы следующие ограничения: в области ![]() выполняются
неравенства
выполняются
неравенства
![]() , (5)
, (5)
где функции ![]() непрерывна при
непрерывна при ![]() , но
, но
![]() , (6)
, (6)
![]() , (7)
, (7)
где функция ![]() непрерывна на
непрерывна на ![]() , однако
, однако
![]() . (8)
. (8)
Тогда для функции ![]() из (4) можно получить
оценку
из (4) можно получить
оценку
![]() , (9)
, (9)
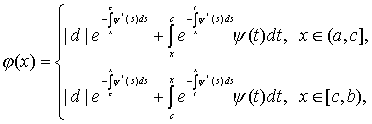 (10)
(10)
причем функция ![]() непрерывна при
непрерывна при ![]() , но
, но
![]() . (11)
. (11)
Обозначим
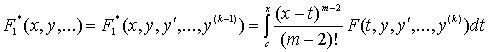 , (12)
, (12)
и будем считать, что уже правая часть (12) ограничена в области ![]() .
.
Если предположить, что функция
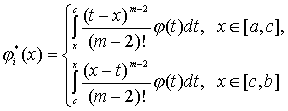 (13)
(13)
так же ограничена на сегменте ![]() , то для
, то для ![]() из (12) имеем оценку
в области
из (12) имеем оценку
в области ![]()
![]() (14)
(14)
в силу которой последнее равенство из (3) с учетом (12), т.е. равенство
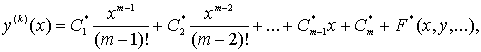 (15)
(15)
![]()
можно рассматривать как интегро-дифференциальное
уравнение ![]() -го порядка и уже без
всяких точек сингулярностей. Все производные выше
-го порядка и уже без
всяких точек сингулярностей. Все производные выше ![]() -го порядка из (3) при
-го порядка из (3) при ![]() ,
, ![]() будут иметь разрывы
бесконечных знаков, поэтому исключаются из дальнейшего рассмотрения в этих
точках при составлении граничных условий, хотя произвольные постоянные
будут иметь разрывы
бесконечных знаков, поэтому исключаются из дальнейшего рассмотрения в этих
точках при составлении граничных условий, хотя произвольные постоянные ![]() , присутствующие в выражениях для них в (3), нами и будут
использованы для задания дополнительных краевых условий с учетом
, присутствующие в выражениях для них в (3), нами и будут
использованы для задания дополнительных краевых условий с учетом ![]() , а иногда и
, а иногда и ![]() , но во внутренних точках интеграла
, но во внутренних точках интеграла ![]() , общее количество которых совпадут с порядком исходного
уравнения (1), т.е. равняется числу
, общее количество которых совпадут с порядком исходного
уравнения (1), т.е. равняется числу ![]() , включая
, включая ![]() условий задачи
Вале-Пуссена для (15):
условий задачи
Вале-Пуссена для (15):
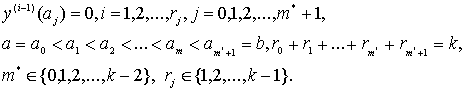 (16)
(16)
Проинтегрируем (15)
последовательно ![]() раз в смысле неопределенного интеграла:
раз в смысле неопределенного интеграла:
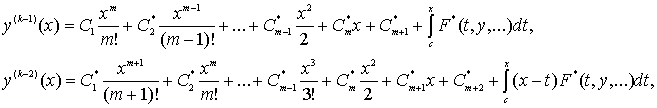
… … …
… … … … ……
… … … … …
… … (17)
… … …
… … … … …… … …
… … … … …
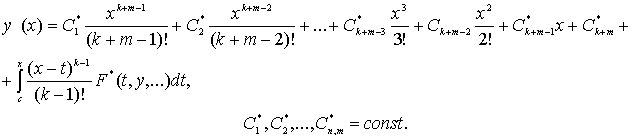
В расшифрованной форме равенства из (16) выглядят так
![]() (18)
(18)
Произвольные
постоянные ![]() согласно (18) и (17)
должны удовлетворять системе алгебраических уравнений
согласно (18) и (17)
должны удовлетворять системе алгебраических уравнений
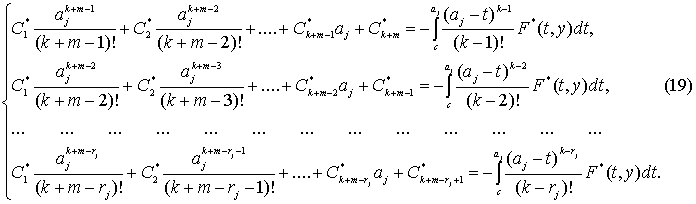 Так как
Так как ![]() , то в системе (19) только
, то в системе (19) только ![]() уравнений. Для построения
недостающихся
уравнений. Для построения
недостающихся ![]() уравнений зададим дополнительные условия с привлечением
уравнений зададим дополнительные условия с привлечением ![]() в виде
в виде
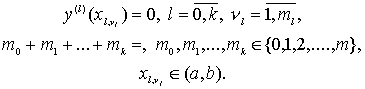 (20)
(20)
В (20) точки
![]() , отличны от точек
, отличны от точек ![]() из (18). Для
граничных условий (20) по примеру (19) из (17) получим еще
из (18). Для
граничных условий (20) по примеру (19) из (17) получим еще ![]() уравнений относительно
уравнений относительно ![]() :
:
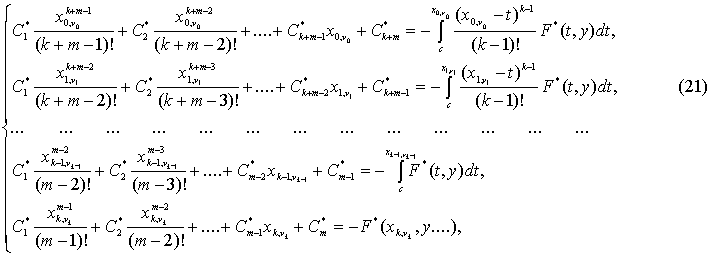
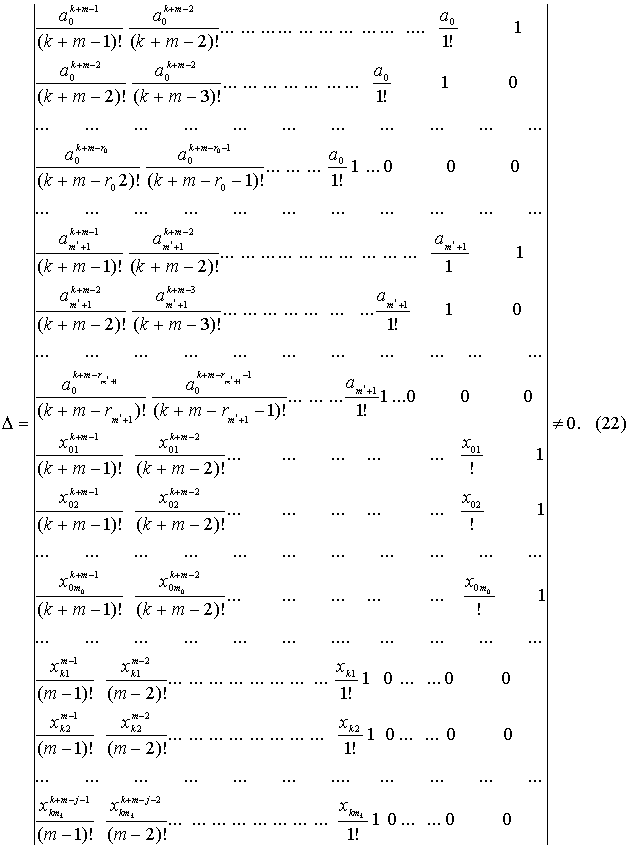
Запишем (15) и (17) в виде единой формулы
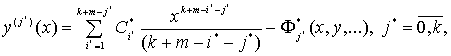 (23)
(23)
где
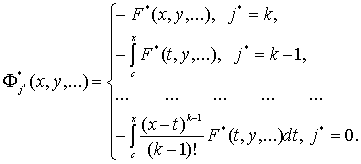 (24)
(24)
Решим
систему (19) и (21) относительно ![]() :
:
![]() (25)
(25)
где ![]() алгебраические дополнения элементов определителя
алгебраические дополнения элементов определителя ![]() ,
,
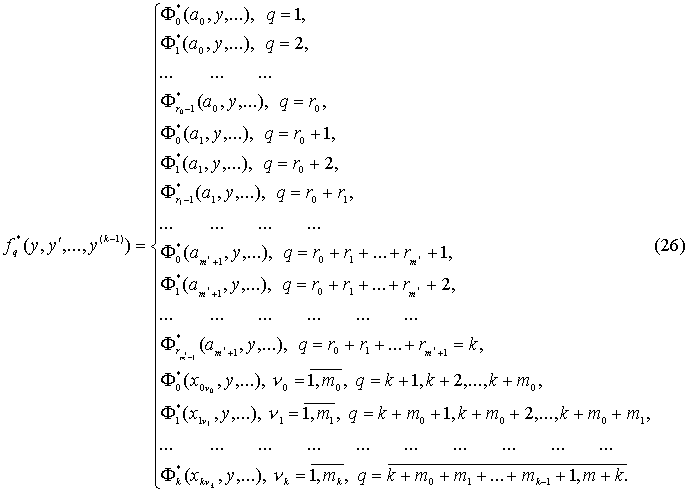
Подставляя выражения для ![]() , из (25) в (23) получим окончательную систему
интегро-дифференциальных уравнений
, из (25) в (23) получим окончательную систему
интегро-дифференциальных уравнений
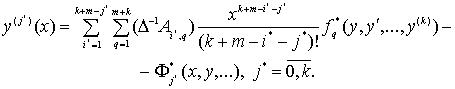 (27)
(27)
Ее будем рассматривать в пространстве к-раз непрерывно-дифференцируемых
функций ![]() с нормой
с нормой ![]() или
или 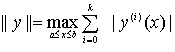 и соответствующими метриками
и соответствующими метриками ![]() для
для ![]()
Обозначим
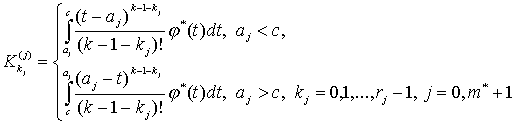 (28)
(28)
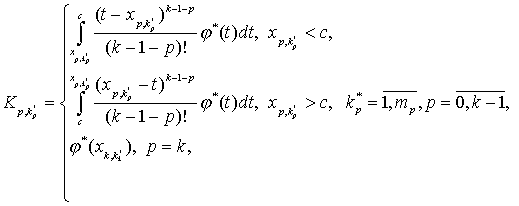 (29)
(29)
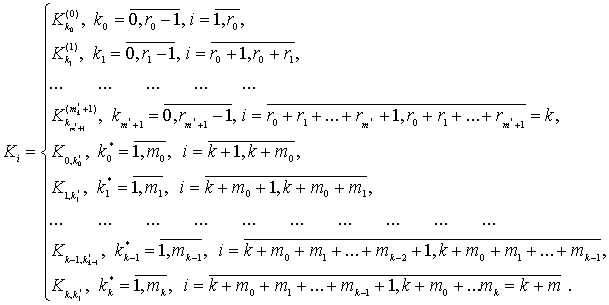 (30)
(30)
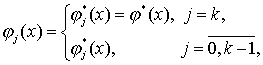 (31)
(31)
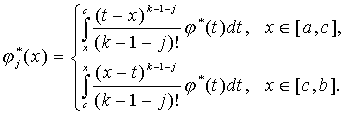 (32)
(32)
Тогда из
(24) и (26) следует (см.(28), (29))
![]() (33)
(33)
![]() . (34)
. (34)
Теперь можно оценить правые части (27) в области ![]()
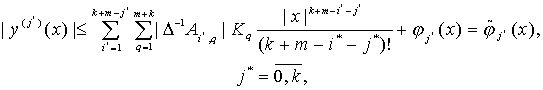 (35)
(35)
где
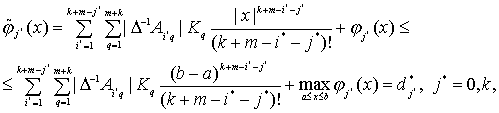 (36)
(36)
где в дальнейшем будет считаться, что выполняются
неравенства
![]() (37)
(37)
Здесь ![]() числа, определяющие область
числа, определяющие область ![]()
В
пространстве ![]() возьмем множество
возьмем множество ![]() функций
функций ![]() , удовлетворяющих следующим условиям:
, удовлетворяющих следующим условиям:
![]() (38)
(38)
для любого положительного числа ![]() можно указать такое
число
можно указать такое
число ![]() , что при
, что при ![]() будут выполняться
неравенства
будут выполняться
неравенства
![]() (39)
(39)
Нетрудно
доказать замкнутость, выпуклость и компактность множества ![]()
Рассмотрим
теперь нелинейный интегро-дифференциальный оператор
![]() (40)
(40)
где ![]()
![]()
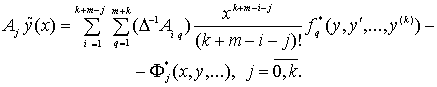 (41)
(41)
В силу (36), (37), оператор А определен на ![]() Покажем, что
Покажем, что ![]()
![]() . Тот факт, что функции
. Тот факт, что функции ![]()
![]() удовлетворяют условиям
(38) проверяется точно также, как мы оценивали (27) при получении (35) и имеем
удовлетворяют условиям
(38) проверяется точно также, как мы оценивали (27) при получении (35) и имеем
![]() (42)
(42)
Пусть ![]() . Из (41) имеем (см.(34)-(36) и (24)):
. Из (41) имеем (см.(34)-(36) и (24)):
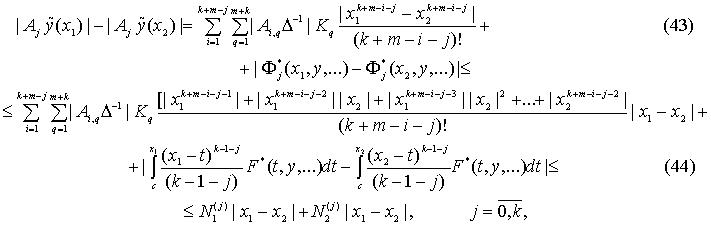
где
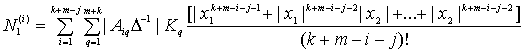
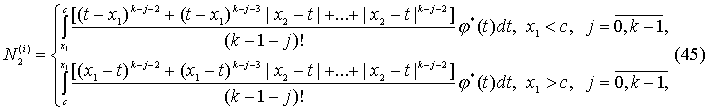
![]()
![]()
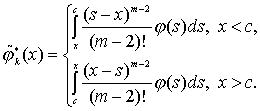 (46)
(46)
Пусть ![]() и
и ![]() любое число.
любое число.
Если подобрать 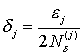 и считать
и считать ![]() , то из (44) имеем неравенства
, то из (44) имеем неравенства
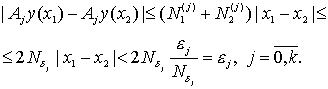 (47)
(47)
Значит, оператор А
преобразует ![]() в себя.
в себя.
Непрерывность оператора А на ![]() вытекает из
непрерывности функций
вытекает из
непрерывности функций ![]() по фазовым
координатам
по фазовым
координатам ![]() и непрерывности
функций
и непрерывности
функций
![]() из (24) в области
из (24) в области ![]() . Поэтому в силу теоремы Шаудера [2] имеем в
. Поэтому в силу теоремы Шаудера [2] имеем в ![]() неподвижную точку,
что означает существование хотя бы одного решения у системы
интегро-дифференциальных уравнений (27). По методу построения системы (27)
ясно, что каждое ее решение удовлетворяет условиям (16) и (20). Так как она
получена последовательным интегрированием исходной системы (1), проделав в
обратном порядке все необходимые действия, приходим к выводу, что каждое
решение задачи (27), (16), (20), будет решением и задачи (1), (16), (20), т.е.
доказана теорема существования решения, которое из-за (2), удовлетворяет еще и
условию
неподвижную точку,
что означает существование хотя бы одного решения у системы
интегро-дифференциальных уравнений (27). По методу построения системы (27)
ясно, что каждое ее решение удовлетворяет условиям (16) и (20). Так как она
получена последовательным интегрированием исходной системы (1), проделав в
обратном порядке все необходимые действия, приходим к выводу, что каждое
решение задачи (27), (16), (20), будет решением и задачи (1), (16), (20), т.е.
доказана теорема существования решения, которое из-за (2), удовлетворяет еще и
условию
![]() . (48)
. (48)
З а м е ч а
н и е. Следует констатировать, что в место условия (7) можно взять и
условие вида
![]() (49)
(49)
где ![]() непрерывна на
непрерывна на ![]() , но
, но
![]() (50)
(50)
Примеры, приведенные в начале изложения
соответствуют условиям (7), (49).
Т е о р е м а. Пусть функция ![]() непрерывна по всем аргументам в области
непрерывна по всем аргументам в области ![]() , а при
, а при ![]() имеют сильные
сингулярности, отраженные в выполненных условий (5)-(12), (14), (15). Пусть
определитель
имеют сильные
сингулярности, отраженные в выполненных условий (5)-(12), (14), (15). Пусть
определитель ![]() в (22) не равняется
нулю и имеют место неравенства (37).
в (22) не равняется
нулю и имеют место неравенства (37).
Тогда
сингулярная краевая задача (1), (16),
(20), (48) имеют по крайней мере одно решение.
Наконец,
необходимо отметить, что структура систем интегро-дифференциальных уравнений
(27) удобна для применения и других принципов неподвижной точки из функционального
анализа и получения теорем единственности решений изучаемой задачи.
Литература
1.
Исраилов С.В. Краевые
задачи для сильносингулярных ОДУ высших порядков //Современные проблемы
математики и смежные вопросы. Материалы Международной конференции «Мухтаровские
чтения», Махачкала, 2008. С.102-104.
2. Исраилов С.В., Юшаев С.С. Многоточечные и
функциональные краевые задачи для
обыкновенных дифференциальных уравнений. Нальчик, Издательский центр «Эль-фа»,
2004. С.445.
Valle-Pussena for strongly-singuljarnyh
differential equations of the higher usages
Israilov
S. V., Sagitov A. A., Yushaev S. S.
In article the nor class of
strong singular equations of special construction is investigated and the
existence theorem solution of boundary problem Valle Pusan: is proven.
Key words: singular, Valle Pusan
problem the existence theorem.
Чеченский государственный
университет (ЧГУ)
Поступила в редакцию 21.02.2011