Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 10. -
Вып. 2. - 2011. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/TITL-30.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/cont.htm
УДК
681.3.001.57
ПРИМЕНЕНИЕ
ДЕРЕВЬЕВ РЕШЕНИЙ В ЗАДАЧАХ ПРОГНОЗИРОВАНИЯ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Ó 2011 г. Волосенков А. В.
Рассматривается задача прогнозирования
многомерных временных рядов. Обосновано применение деревьев решений для анализа
дискретного многомерного временного ряда с неизменными во времени
статистическими свойствами. Описаны способы построения деревьев решений и
проведен их сравнительный анализ.
Ключевые слова: временной ряд, дерево
решений, процесс, прогнозирование.
Одной из важных задач во
многих отраслях промышленности является задача прогнозирования возникновения
нештатных ситуаций в многомерной среде временных рядов. Например, на
нефтеперерабатывающих заводах сотни датчиков переменных процессов установлены
на различных участках блоков обработки. В процессе мониторинга за критическими
переменными, существенно влияющими на работу, при срабатывании сигнала тревоги
бывает слишком поздно, чтобы выполнить корректирующее действие. Это может привести
к снижению качества продукта, или аварии. Таким образом, большое значение имеет
задача прогнозирования возникновения
нештатных ситуаций предсказание того, когда эти критические переменные
достигнут нежелательных диапазонов. В этом случае инженеры могут иметь
достаточно времени для принятия необходимых мер.
Традиционно, инженеры и
исследователи пытались построить математические модели, чтобы понять физический
процесс и определить временные отношения между переменными. Однако в задачах
прогнозирования многомерных временных рядов имеется множество переменных, и
анализ их взаимодействия является чрезвычайно сложным процессом. Построение
точной математической модели очень затруднительно, а иногда и невозможно.
Процедуры оценки параметров и прогнозирования, зачастую предполагают, что
математическая модель процесса известна. Однако исследования в данной области
свидетельствуют, что в данных нет отчетливо выраженных регулярных составляющих,
и поэтому возникает необходимость построения прогностической модели
непосредственно из многомерных временных рядов [1]. В этих целях используются
деревья решений в задачах прогнозирования временных рядов. Рассмотрим подробнее
сами деревья и способы их построения.
Пусть для описания
некоторого объекта исследования используется набор случайных характеристик 
значения которых меняются с
течением времени. Характеристики могут быть как количественными, так и
качественными.
Пусть характеристики
измеряются в последовательные моменты времени 
.. . Для определенности будем предполагать, что измерения проводятся
через равные интервалы времени. Обозначим через 
значение характеристики 
в момент времени 
. Таким образом, имеем n-мерный разнотипный временной ряд 
Пусть выбрана некоторая
прогнозируемая характеристика 
. Обозначим, для удобства, эту характеристику через 
. Характеристика 
может быть как количественной,
так и качественной.
Рассмотрим произвольный
момент времени 
, а также набор предыдущих моментов времени 
, где 
- некоторая заданная величина
(лаг или «глубина предыстории»), 
. Будем полагать, что условное распределение 
, при условии, что заданы все предыдущие значения 
, зависит только от значений ряда в 
предыдущих моментов времени.
Кроме того, предположим, что
эта зависимость одна и та же для любых 
. Данное предположение означает, что статистические свойства ряда,
определяющие зависимость, неизменны во времени.
Для произвольного момента
времени 
можно образовать набор 
представляющий собой реализации
временного ряда в 
предшествующих моментов
времени. Набор 
назовем предысторией длины 
для момента 
.
Требуется построить модель
зависимости характеристики 
от ее предыстории для
произвольного момента времени. Модель позволяет прогнозировать значение
характеристики 
в будущий момент времени по
значениям характеристик за 
прошлых моментов. Иначе говоря,
данная модель представляет собой решающую функцию для прогнозирования по
предыстории.
В зависимости от типа
характеристики 
можно рассматривать различные
типы задач прогнозирования.
1. 
– качественная
характеристика. Задачу данного типа, по аналогии с обычной задачей
распознавания образов, назовем задачей распознавания динамического объекта.
Анализируемый объект может с течением времени менять соответствующий
ему образ.
2. 
– количественная характеристика: В этом случае имеем задачу прогнозирования количественной
характеристики объекта.
Решающую функцию для
прогнозирования временного ряда по его предыстории будем представлять в виде
дерева решений. В нем проверяются высказывания относительно некоторых характеристик
в некоторый j-й предыдущий отсчет
времени. Для удобства, будем обозначать эти характеристики, с учетом
предыстории, через 
(рисунок 1). Таким образом, 
означает «характеристика 
в j-й предыдущий момент времени (относительно текущего момента).
Итак, пусть имеется набор
измерений характеристик 
в моменты времени 
и задано значение 
. Таким образом, имеем
многомерный разнотипный временной ряд длины 
. Сформируем множество всех предысторий длины 
для моментов времени 
.
Для любого заданного дерева
решений в задаче прогнозирования по предыстории можно определить его качество.
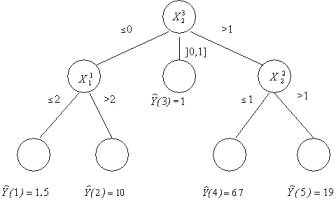
Рисунок 1 – Пример дерева
решений
Для обычного дерева:
обозначим через 
прогнозируемое значение 
, полученное с помощью дерева по предыстории 
, тогда критерий качества будет
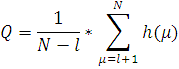
где
для задачи
распознавания динамического
объекта;
для
задачи прогнозирования количественной характеристики.
Будем считать, что данный
ряд используется для «обучения» прогнозированию.
Пусть имеется ряд 
длины 
, 
. Тогда можно сравнить полученные в результате обучения прогнозируемые
значения 
с «истинными» значениями 
и определить погрешность
прогноза. В этом случае будем говорить, что данный ряд используется для
«контроля» качества прогнозирования.
Опишем несколько способов,
при использовании которых исходная задача построения дерева решений разбивается
на ряд более простых задач распознавания образов или регрессионного анализа, в
зависимости от типа прогнозируемой характеристики Y.
Набор 
представим в виде таблицы 
, содержащей 
строк и 
столбцов. Тогда исходной
информацией для прогнозирования является набор таблиц 
, вместе с указанными для каждой таблицы значениями прогнозируемой
характеристики 
.
Mножество 
можно представить в виде
трехмерной таблицы размерности 
, которой будет соответствовать
вектор 
(рисунок 2). Однако имеющиеся
методы распознавания или
регрессионного анализа с
использованием деревьев решений используют в качестве входной информации
двумерные таблицы [2].
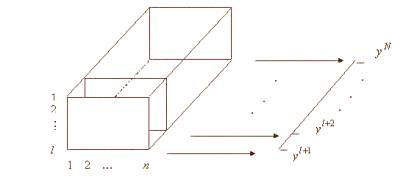
Рисунок 2 –
Трехмерная таблица размерности
Можно указать несколько
различных способов использования данных методов для решения задачи анализа
трехмерных таблиц данных.
Каждая таблица 
представляется в виде строки
соответствующих значений характеристик
(иначе говоря, таблица просто
«вытягивается» в строку).
В результате получаем
двумерную таблицу размерности 
, для которой затем строится решающая функция, представленная в виде
дерева решений.
Данный способ очень прост в
реализации, однако, как показывают исследования, полученные решения, в условиях
большого числа характеристик, большой длины предыстории и сравнительно малой
длины ряда, могут оказаться неустойчивыми, т.е. будут давать большую ошибку на
контрольном ряде (известно, что эффект неустойчивости проявляется при малом
объеме выборки и большом числе характеристик).
Исходная задача решается в
два этапа.
На первом этапе
рассматриваются 
двумерных таблиц вида 
, где 
принимает значения 
– значения 
– значения 
образованных «горизонтальными»
срезами исходной трехмерной таблицы
данных (рисунок 3).
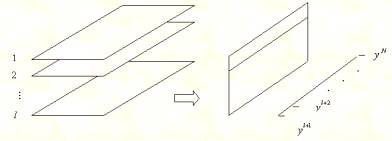
Рисунок 3 – Срезы трехмерной
таблицы данных
Строятся 
различных деревьев решений для предсказания величины 
по каждой из данных таблиц.
Каждая из таблиц, с помощью построенного дерева, «свертывается» в одномерную
строку символов (каждый символ кодируется номером соответствующей конечной
вершины дерева). Таким образом, получается двумерная таблица, для которой на втором
этапе снова строится дерево решений. Затем каждый символ обратно преобразуется
в соответствующую цепочку высказываний.
3. Задача решается также в
несколько этапов.
1) Рассматриваются 
таблиц вида 
, где 
принимает значения
– значения 
– значения 
, и затем 
таблиц вида 
, где 
принимает значения 
– значения 
– значения 
. Таким образом, имеем 
«горизонтальных» и 
«вертикальных» срезов исходной
таблицы (рисунок 4). Для каждой
из полученных двумерных таблиц строится дерево решений. В итоге получаем набор
деревьев 
. Обозначим через 
наилучшее из этих деревьев.
2) Рассматриваются все
конечные вершины дерева 
и выделяются те из них, для которых
ошибка прогнозирования превышает заданную величину. Для каждой из этих вершин
формируется соответствующий набор предысторий 
и далее процесс достраивания
дерева для 
повторяется, начиная с п.1).
Рисунок 4 –
Результирующий набор деревьев
3) Процесс продолжается до
тех пор, пока на некотором шаге полученное дерево не будет удовлетворять
условию окончания (т.е. если число конечных вершин достигнет определенной
величины 
, либо ошибка прогнозирования станет меньше заданного значения).
Можно заметить, что данный
способ отличается от предыдущего пошаговым достраиванием дерева решений для
прогнозирования.
Построенные деревья решений
были протестированы на реальных данных, результаты эксперимента
свидетельствуют, что они выполняют достаточно точные прогнозы [1].
Таким образом, применение
деревьев решений в задачах прогнозирования многомерных временных рядов является
практически обоснованным.
Литература
1. B.Liu and J.Liu .Multivariate Time Series Prediction via Temporal
Classification. // Proceeding of the 18th International Conference on Data
Engeneering. Computer Society. Vol 2, 2002, pp.17.
2. Lbov, G. and Berikov, V. Recognition of a Dynamic Object and
Prediction of Quantitative Characteristics
in the Class of Logical Functions. // Pattern Recognition and Image Analysis. Vol 7, N 4, 1997, pp. 407-413.
APPLICATION OF TREES OF DECISIONS IN PROBLEMS OF FORECASTING OF
MULTIDIMENSIONAL TIME NUMBERS
Volosenkov
A.V.
The problem of
forecasting of multidimensional time numbers is considered. Application of
trees of decisions for the analysis of a discrete multidimensional time number
with invariable in time statistical properties is proved. Ways of construction
of trees of decisions are described and their comparative analysis is carried
out
Key words: A time number, tree of decisions, process, forecasting.
Филиал ГОУВПО Московский
энергетический институт
(Технический университет) в г. Смоленске
Поступила в редакцию
30.03.2011.