Поступила в редакцию

Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 10. -

Вып. 2. - 2011. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/TITL-30.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/cont.htm

УДК 621.396.61(075)

МЕТОДИКА РАСЧЕТА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ УПОРНОГО ИЗЛУЧАТЕЛЯ АНТЕННОЙ РЕШЕТКИ

Ó 2011 г. Зайцев А. В., Амозов Е. В., Земцов А. В., Битаев Е. С.

(zaitsev.doc)

В настоящее время существует ряд сложностей возникающих при расчёте сверхширокополосных рупорных антенн. В статье рассмотрен вопрос расчета электромагнитного поля в указанной точке пространства. Предложена математическая модель электромагнитного поля сверхширокополосного излучателя рупорной антенной решетки.

Ключевые слова: сверхширокополосная рупорная антенна, электромагнитное поле, антенная решётка.

В процессе разработки сверхширокополосных рупорных антенн возникает проблема расчета электромагнитного поля в указанной точке пространства.

На рис. 1 изображена пирамидальная рупорная антенна с питающим волноводом. Данная антенна состоит из раструба и питающего волновода. Наиболее узкополосным элементом является питающий волновод, обладающий полосой пропускания ограниченной длинами волн от 2*а до а, где а – размер широкой стенки волновода.

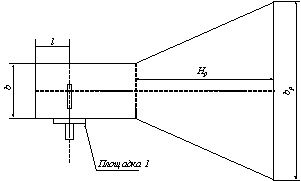
Рисунок - 1 Пирамидальная рупорная антенна

На вход питающего волновода сечением 55 мм подается сигнал Е₀, представляющий собой гармонические колебания на частоте f_н = 6,5 ГГц, модулированные по амплитуде гауссовым импульсом длительностью τ = 0,4 нс (рис. 2):

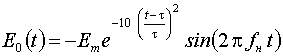Сигнал Е₀ раскладывается на спектральные составляющие. Далее вычисляется скорость распространения каждой составляющей сигнала в прямоугольном волноводе

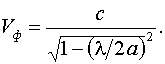
Зависимость скорости распространения сигнала от длины волны приводит к изменению фазы сигнала:

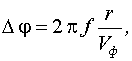
где r – длина волновода.

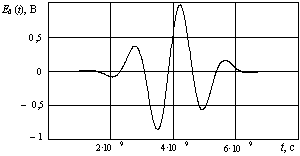
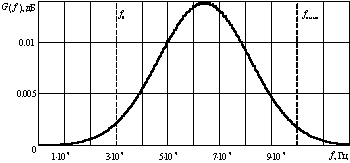
Рисунок - 2 а) Сигнал на входе питающего волновода; б) Спектр сигнала Е₀

Кроме того, учитывается коэффициент затухания

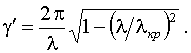
Спектр сигнала в раскрыве антенны описывается выражением

где G₀ – амплитуда спектральной составляющей.

Затем производится обратное преобразование Фурье с учетом этих изменений и вычисляется сигнал на выходе волновода. Оцениваются изменения его длительности и амплитуды колебаний. При прохождении СШП сигнала по волноводу длиной 200 мм его длительность увеличилась в 2 раза, а амплитуда колебаний изменилась в среднем на 5 % (рис. 3).

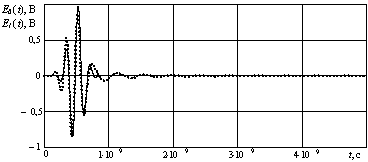
Рисунок - 3 Сигналы на входе и выходе волновода длиной 200 мм

Дальнейшее увеличение длины волновода приводит к еще большим изменениям его длительности и амплитуды (рис. 4).

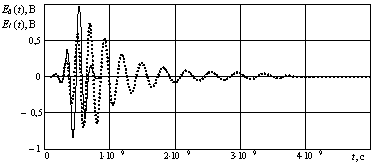
Рисунок - 4 Сигналы на входе и выходе волновода длиной 1000 мм

Погрешность в расчетах, определяемая по соотношению энергии сигнала на входе и на выходе волновода, составила 0,017 %.

Для снижения трансформации СШП сигнала предлагается из классической конструкции рупорной антенны исключить возбуждающий волновод и поместить возбуждающий штырь непосредственно в раструб рупора (рис. 5).

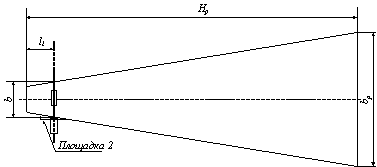
Рисунок - 5 Усеченная пирамидальная рупорная антенна

Возбуждающий штырь должен располагаться параллельно задней стенке рупора, по аналогии с расположением в питающем волноводе. Это достигается при помощи площадки 2, угол среза которой соответствует углу раскрыва рупора. Сечение рупора в точке питания выбирается, исходя из требуемой нижней границы частотного диапазона излучателя: . Размеры раскрыва рупора определяются, исходя из необходимой ширины диаграммы направленности излучателя. Высота рупора Н_р рассчитывается так, чтобы раскрыв рупора возбуждался равномерно на верхней границе частотного диапазона [1].

Электромагнитное поле рупорной антенны, при излучении гармонических сигналов, рассчитывается по формулам:

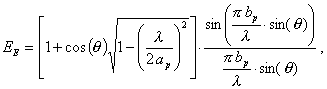
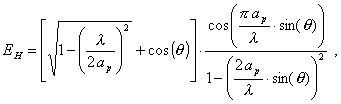
где а_р и b_р – размеры широкой и узкой стенки рупора в раскрыве.

Использование данных зависимостей при излучении негармонических сигналов затруднительно из-за необходимости расчета поля для каждой частотной составляющей сигнала. Это значительно увеличивает вычислительные затраты. Поэтому предлагается использовать апертурный метод расчета нестационарного электромагнитного поля, основанный на принципе Гюйгенса-Кирхгофа. Который заключается в том, что поле в любой точке пространства может быть однозначно определено по заданным тангенциальным составляющим векторов и на замкнутой поверхности S. При условии, что источники тока и точка наблюдения лежат по разные стороны поверхности S. Принцип Гюйгенса-Кирхгофа записывается следующим образом:

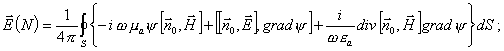
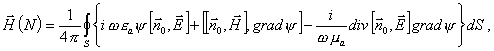
где

y = е ^–^b^r/r; r

–

расстояние от точки наблюдения до текущей точки на поверхности S;

–

орт нормали к поверхности S, направленный в ту часть пространства, в котором находится точка наблюдения.

Данные выражения позволяют определять электромагнитное поле в пространстве по заданным электромагнитным полям на некоторой поверхности [2].

Во временной области, согласно принципу суперпозиции электромагнитное поле, создаваемое всей поверхностью некоторого раскрыва произвольной формы S складывается из полей элементарных площадок dS (рис. 6):

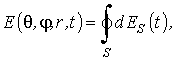
где		–	поле элементарной площадки Гюйгенса на поверхности раскрыва произвольной формы;
		–	первая производная по времени возбуждающего поля в раскрыве антенны с учетом времени запаздывания t = t_з – r'/c, затраченного на распространение волн от элементов раскрыва dS до точки наблюдения;
	r' = r – ρ' sin θ cos (j – j')	–	расстояние от точки наблюдения до элементов поверхности раскрыва антенны;

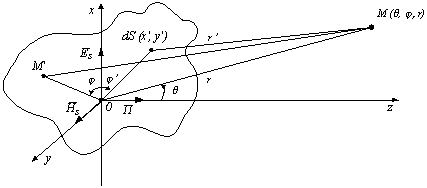
Рисунок – 6 расчету поля раскрыва произвольной формы

При расчете электромагнитного поля, создаваемого раскрывом прямоугольной формы, например, раскрывом рупорной антенны, выражение примет следующий вид:

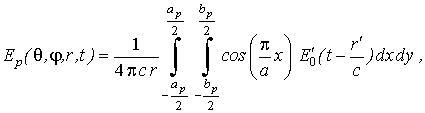
где а_р и b_p – размеры раскрыва рупорной антенны.

Полученные выражения являются математической моделью электромагнитного поля сверхширокополосного излучателя рупорной антенной решетки.

Используя предлагаемую математическую модель электромагнитного поля сверхширокополосного излучателя рупорной антенной решетки, можно определить создаваемое им электромагнитное поле в любой точке пространства.

литература

1. Зайцев А. В. Исследования электромагнитных полей во временной области. Научно–технический и теоретический журнал «Антенны». Москва. 2001. С. 3–10.

2. Иммореев И. Я., Синявин А. Н. Излучение сверхширокополосных сигналов// Сб. «Антенны». М., Радио и связь, 2001. Вып. 1.

3. Нефёдов Е. И. Устройства СВЧ и антенны. М., «Академия», 2009. 384 с.

ELECTROMAGNETIC FIELD CALCULATIONS FOR ARRAY HORN RADIATORS

Zaitsev A., Bitaev E., Amozov E., Zemtsov A.

Presently, calculations related to ultrawideband (UWB) horn antennas present a number of difficulties. The given article deals with electromagnetic field calculations in certain point. Also, the authors offer mathematical model for electromagnetic field of UWB horn array's radiator.

Key words: UWB horn antenna, electromagnetic field, antenna array.

Военная академия войсковой ПВО Вооруженных Сил Российской Федерации

имени Маршала Советского Союза А.М. Василевского

(ВА ВПВО ВС РФ)

Поступила в редакцию 20.03.2011.