Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 10. -

Вып. 2. - 2011. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/TITL-30.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-30-html/cont.htm

УДК 621.372(075)

МЕТОДИКА ВЕЙВЛЕТ-КЕПСТРАЛЬНОЙ ОБРАБОТКИ ДИСКРЕТНЫХ СИГНАЛОВ

Ó 2011 г. Жбанов И. Л., Силаев Н. В., Бондаренко Д. Л.

(zhbanov-2.doc)

В данной статье рассмотрена проблема использования алгоритма кепстральной обработки при определении временных задержек в дискретных сигналах. Предложен новый подход при выделении временных задержек. Путем математического моделирования исследовано влияние различных факторов на работоспособность и характеристики метода.

Ключевые слова: вейвлет-кепстральная обработка, временная задержка.

Во многих областях науки и техники приходится сталкиваться с проблемой обработки сигналов, представляющих собой сумму исходного (зондирующего) сигнала и сигнала отраженного от различных объектов на величину (рисунок 1), где – длительность сигнала. Однако наиболее простым с точки программной реализации и эффективным алгоритмом позволяющем определить временную задержку при ее минимальном значении равном является алгоритм кепстральной обработки (рисунок 2) [1].

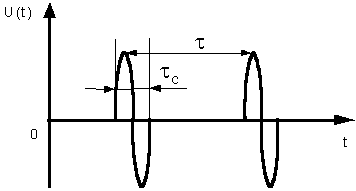
Рисунок 1 – Сигнал и сдвинутая относительно него на время его копия

Данный вид обработки представляется в виде алгоритма показанного на рисунке 2 и основан на логарифмически–спектральном преобразовании входного сигнала*.

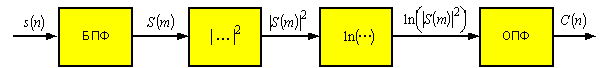
Рисунок 2 – Алгоритм кепстральной обработки сигналов

Рассмотрим работу данного алгоритма на примере. Пусть – суммарный сигнал, действующий на входе кепстрального алгоритма обработки. В результате быстрого преобразования фурье (БПФ) и поставленного ему в соответствие некоторое z преобразование данный сигнал примет вид описываемый по выражением (1) (рисунок 3).

(1)

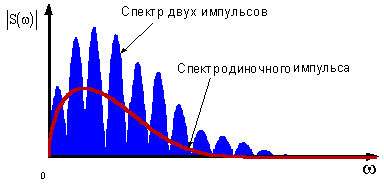
Рисунок 3 – Спектр входного сигнала

Если вынести за скобки, а остаток представить в виде сигнала то полученное произведение можно представить как свертку двух функций времени описываемых выражением (2)

(2)

где – сигнал z преобразование, которого равно.

В результате сигнал можно представить в виде суммы двух дельта функций (3) (рисунок 4).

. (3)

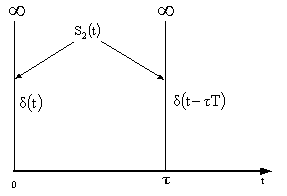
Рисунок 4 – Сигнал

Сигнал в процессе раскрытия скобок примет вид:

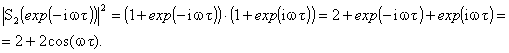(4)

Таким образом, исходный сигнал будет описываться выражением (5):

. (5)

В результате логарифмирования выражения (5) возможен переход от произведения двух слагаемых к их сумме исходя из основных свойств логарифма рисунок 5. На рисунке 6 представлена каждая составляющая данной суммы в отдельности. В результате можно заключить, что слагаемое определяет закон модуляции спектра энергии с периодом , а слагаемое его огибающею.

В последующем в результате обратного преобразования Фурье от результата логарифмирования

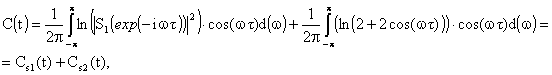
будет получен сигнал, именуемый кепстром представленный на рисунке 6. Однако стоит подчеркнуть, что по оси ординат откладывается особое кепстральное время получившее свое название сочастота [1].

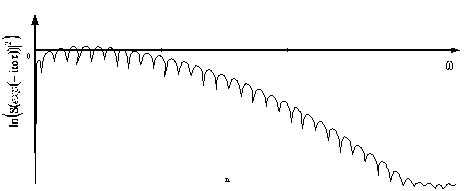
Рисунок 5 – Изображение результата логарифмирования

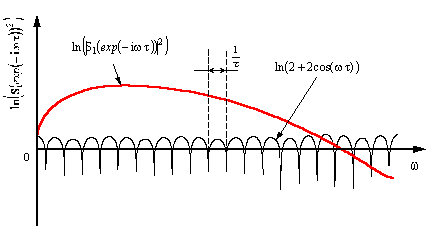
Рисунок 6 – Изображение отдельно каждого элемента результата логарифмирования

В результате первый пик по оси сочастот соответствует искомой временной задержке . Появление же ложных пиков можно пояснить на следующем примере: рассмотрим значение второго сигнала , которое можно представить исходя из свойства логарифма в следующем виде

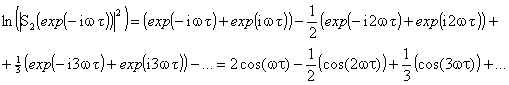(6)

Подставив этот результат во второе слагаемое результата обратного преобразования Фурье получим следующие выражение

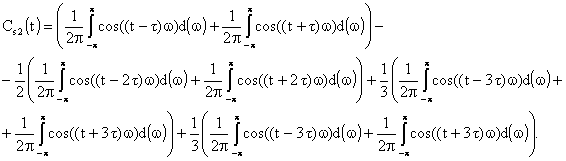
Очевидно, что отлично от нуля только в точках , и т.д, причем ,, и т.д.

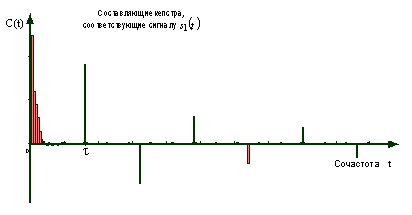
Рисунок 7 – Результат обратного преобразования Фурье

Однако при сложной форме сигнала, низком отношении сигнал/шум и небольшом значении временной задержки (рисунок 8), возможны ситуации когда составляющие кепстра соответствующие сигналу перекрывают составляющие кепстра соответствующие сигналу , как показано на рисунке 9, в результате чего возможна ошибка при определении временной задержки по первому пику.

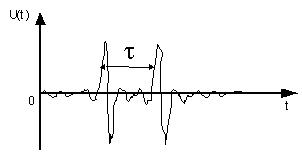
Рисунок 8 – Сигнал и сдвинутая относительно него на время его копия в шумах

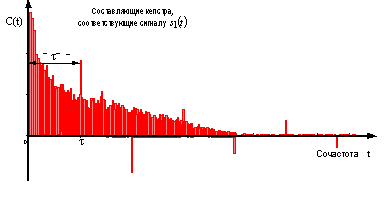
Рисунок 9 – Результат обратного преобразования Фурье при низком отношении сигнал/шум

Очевидно, что для избегания подобных ситуаций необходим алгоритм способный исключать составляющею кепстра соответствующею сигналу независимо от его формы, повышая тем самым адаптивность кепстральной обработки к форме исследуемого сигнала.

Для решения поставленной задачи фильтрации составляющей кепстра соответствующей сигналу от составляющей кепстра соответствующей сигналу , необходимо постоянное знание формы сигнала, что делает предлагаемый способ выделения информации не адаптивным, а это противоречит условиям поставленной задачи и неприемлемо. Однако исследуя спектр исходного сигнала (рисунок 3) можно с уверенностью предположить, что логарифм квадрата модуля спектральной плотности одного импульса будет носить низкочастотный характер, а логарифм квадрата модуля спектральной плотности сигнала состоящий из двух дельта-функций высокочастотный характер, в любом случае и независимо от формы сигнала. В связи с этим заключением, логично предположить о необходимости использования некоторого алгоритма, позволяющего производить разложение исходного сигнала на две составляющие, высокочастотную и низкочастотную, с целью дальнейшего удаления ненужной при обратном преобразовании Фурье в алгоритме кепстральной обработки сигнала.

Анализ теории гармонических сигналов показал, что данная задача на сегодняшний момент решается при помощи вейвлет преобразования [2], которое является разновидностью спектрального анализа, а роль простых колебаний в нем играют функции особого рода, называемые вейвлетами. Английское слово wavelet (от французского «ondelette») дословно переводится как «короткая (маленькая) волна». В различных переводах зарубежных статей на русский язык встречаются еще термины: «всплеск», «всплесковая функция», «маловолновая функция», «волночка» и др.

В общем вейвлет-преобразование (ВП) сигнала – это его представление в виде обобщенного ряда или интеграла Фурье по системе некоторых базисных функций вида (7)

, (7)

сконструированных из материнского (исходного) вейвлета , обладающего определенными свойствами за счет операций сдвига во времени (b) и изменения временного масштаба (a). Множитель обеспечивает независимость нормы этих функций от масштабирующего числа a. На рисунке 10, для примера изображен процесс сдвига и растяжения материнского вейвлета «мексиканская шляпа».

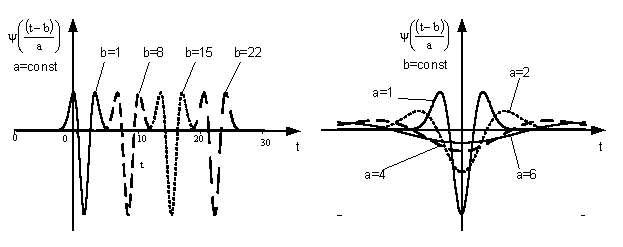
Рисунок 10 – Сдвиг и растяжение вейвлета «мексиканская шляпа»

Стоит отметить, что на сегодняшний день известно уже множество семейств вышеупомянутых функций, основной отличительной особенностью которых является, прежде всего, соответствие некоторым основным свойствам, а именно:

– квадрат нормы функции должен быть конечным (ограниченность)

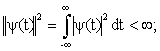
–функции должна быть локализована во времени;

– интеграл от функции должен быть равен нулю

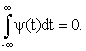
Однако так как использование вейвлет анализа, для обработки сигналов предполагается в цифровом виде, рассмотрим далее принципы его работы на основе дискретного вейвлет преобразования.

И так, пусть дан некоторый дискретный сигнал , где n – номер отчета во временной области, тогда прямое дискретное вейвлет-преобразование данного сигнала примет вид [3]

, (8)

где N – число отсчетов в дискретном сигнале U(n) кратное двум.

В результате получаемые коэффициенты будут представлять собой двумерный массив данных , размером a на b, причем количество столбцов а (количество возможных сжатий материнского вейвлета) в данном массиве будет определяться из выражения (2.8)

, (9)

где k – степень, в которую необходимо возвести число 2 чтобы получить N.

Другими словами количество растяжений материнского вейвлета представляют собой уровни разложения сигнала по возрастанию. А количество строк b (количество сдвигов) будет совпадать с количеством отсчетов сигнала U(n). В результате каждый столбец, начиная с первого, в двумерном массиве , будет включать в себя все меньше высокочастотных коэффициентов исходного сигнала U(n), по мере растяжения материнского вейвлета.

Так как обратное дискретное вейвлет-преобразование вычисляется по формуле (10)

, (10)

в результате подавление некоторых элементов масштабного ряда k, при обратном восстановлении сигнала U(n), возможно осуществлять фильтрацию входного сигнала по его составляющим. Так при обнулении первых нескольких значений масштабного ряда k возможно восстановление низкочастотных составляющих сигнала U(n), а при обнулении нескольких значений в конце масштабного ряда k возможно восстановление высокочастотной составляющей сигнала U(n). Другими словами, управляя растяжением и сжатием материнского вейвлета возможно осуществлять выбор необходимых составляющих сигналов при обратном вейвлет преобразовании.

К тому же стоит отметить, что имея значения исходного сигнала U(n) в конкретных точках и значения в этих же точках одной из составляющей этого сигнала, на основе элементарного вычитания можно получить значения в этих же точках второй составляющей этого сигнала. Таким образом, благодаря вейвлет-преобразованию, возможно, производить разложение сигнала на его высокочастотную и низкочастотную часть.

На основе полученных знаний о вейвлет преобразовании была разработана методика вейвлет-кепстрального преобразования по подавлению низкочастотной составляющей сигнала , представленную в виде функциональной схемы на рисунке 11.

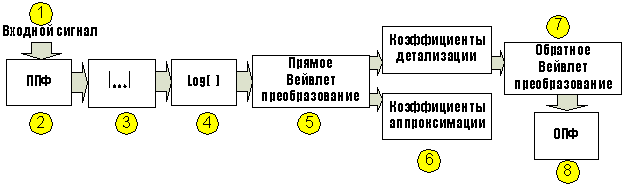
Рисунок 11 – Схема, реализующая вейвлет-кепстральную обработку

1. Для наглядности продемонстрируем работу методики вейвлет-кепстральной обработке на примере выделения высокочастотно и низкочастотной составляющей из дискретного сигнала представляющего собой результат логарифмирования на выходе блока логарифмирования для сигнала, представленного на рисунке 5, алгоритма кепстральной обработки (рисунок 11).

2. Причем количество отсчетов n, пусть равно 256 исходя из условия (9).

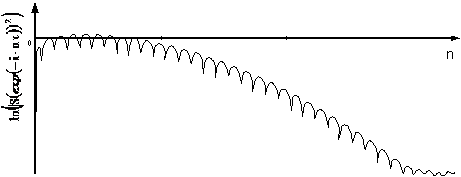
Рисунок 12 – Вид сигналов и

3. В качестве вейвлета используем вейвлет «мексиканская шляпа», описываемый выражением (10) (рисунок 13).

(11)

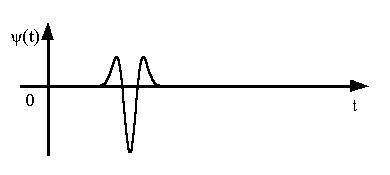
Рисунок 13 – Вид вейвлетов

4. На основании выражения (8) будет получена матрица коэффициентов вейвлет преобразования , проанализируем ее графическое отображение (рисунки 14).

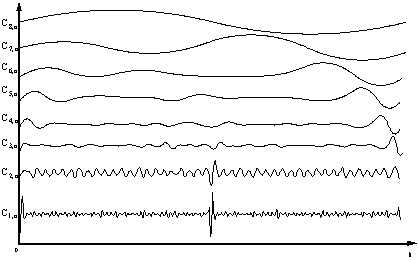
Рисунок 14 – Вид коэффициентов

5. Анализируя рисунок 14 можно сказать, что основная часть коэффициентов несущих информацию о высокочастотной составляющей содержится в коэффициентах до четвертого уровня, поэтому обнуляя их и используя сумму остальных, при обратном дискретном вейвлет преобразовании (12) получим низкочастотную составляющею исходного сигнала (рисунок 15).

(12)

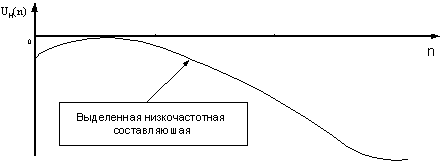
Рисунок 15 – Вид низкочастотная составляющая сигнала

Стоит также отметить, что учет лишь одного из высокочастотных коэффициентов ведет к существенному ухудшению формы выделяемого сигнала (рисунок 16).

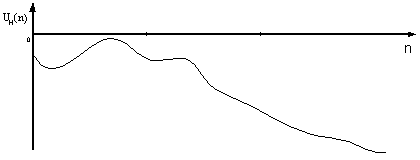
Рисунок 16 – Вид низкочастотной составляющей сигнала с учетом лишь одного из высокочастотных коэффициентов детализации

6. И так, исходя из вышесказанного проделав те же операции с квадратом модуля логарифма спектра исходного сигнала (1), возможно решить обратную задачу, для удаления его низкочастотной составляющей по выражению (13) (рисунок 17), что позволит повысить отношение сигнал шум на выходе кепстральной обработке (рисунок 18).

(13)

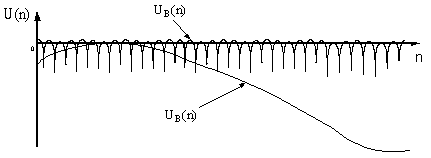
Рисунок 17 – Результат действия вейвлет-преобразования по подавлению низкочастотной составляющей квадрата модуля логарифма спектра исходного сигнала

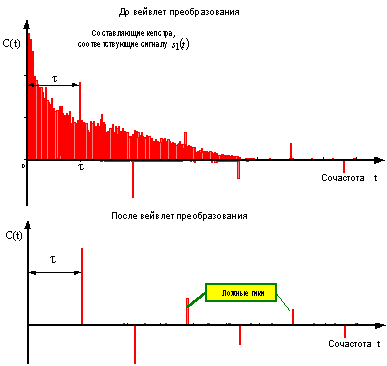
Рисунок 18 – Сравнение результатов действия вейвлет-преобразования по подавлению низкочастотной составляющей квадрата модуля логарифма спектра исходного сигнала на выходе алгоритма кепстральной обработки

Работоспособность предложенной методики вейвлет-кепстральной обработки, проверена при помощи предложенной математической модели (ММ) системы передачи данных (СПД), которая включала ММ последовательности двух одинаковых импульсов (произвольной формы), передающей антенны, канала связи, приемной антенны и ММ предлагаемого метода. Для получения ММ приемной и передающей антенны использовалась лабораторная установка, состоящая из генератора СШП импульсов TMГ075045ВО01, стробоскопического осциллографа ТМР8220 и двух идентичных СШП рупорных антенн (рисунок 19).

Рисунок 19 – Лабораторная установка

На основе измеренных с помощью стробоскопического осциллографа параметров последовательности импульсов на выходе генератора и приемной антенны осуществлялся расчет импульсных характеристик приемной и передающей антенн. При этом приемная и передающая антенна рассматривались в виде четырехполюсников с одинаковыми коэффициентами передачи. На основе теории четырехполюсников находились импульсные характеристики приемной и передающей антенн, используемые затем в ММ СПД. Предложенные ММ позволяли исследовать работоспособность предложенного метода в условиях помех различной интенсивности. Для этого в ММ канала связи осуществлялось сложение, ММ последовательности двух одинаковых импульсов (произвольной формы) с шумом, распределенным по нормальному закону с нулевым математическим ожиданием и различной дисперсией. Результаты выделения временной задержи при различном отношении сигнал-шум Q на входе приемной антенны, представлены в табл. 1

Табл. 1- Зависимость вероятности выделения временной задержки по предложенной методике от отношения сигнал-шум на входе приемной антенны

Отношение сигнал/шум Q ,[разы]	1	5	10	15	20
Вероятность выделения временной задержки	0,508	0,901	0,995	0,999	0,999

литература

1. Гоноровский И.С. Радиотехнические цепи и сигналы.– М.: Радио и связь, 1986. 477 с.

2. Смоленцев Н.К., Основы теории вейвлетов. Вейвлеты в MATLAB: Издание третье. – М.: Прикладная математика, 2008. 126 с.

TECHNIQUE WAVELETS-CAPSTRAL OF PROCESSING OF DISCRETE SIGNALS

Zhbanov I. L., Silaev N. V., Bondarenko D. L.

In given clause the problem of use of algorithm capstral of processing is considered at definition of temporary delays in discrete signals. The new approach is offered at allocation of temporary delays. By mathematical modeling the influence of the various factors on serviceability and characteristics of a method is investigated.

Key words: wavelets-capstral of processing, temporary delay.

Академия войсковой ПВО Вооруженных Сил РФ

им. Маршала Советского Союза А. М. Василевского, г. Смоленск

Поступила в редакцию 30.03.11.