Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 10. -
Вып. 3. - 2011. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-31-html/TITL-31.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-31-html/cont.htm
УДК 37.0:004
ББК 74.580.255
Построение
модели системы учебных заданий средствами графового моделирования
Ó
2011 г. Бояринов Д. А.
В статье излагается подход к построению графовых
моделей систем учебных заданий.
Ключевые
слова: задача,
система задач, графовая модель, диаметр задачи.
Эффективное применение
графового моделирования в процессе обучения в рамках информационного
образовательного пространства предполагает, в частности, разработку формальных
моделей, позволяющих описать процесс обучения решению задач. В свою очередь,
для этого необходимо дать в терминах теории графов серию определений, в первую
очередь взаимосвязанные определения задачи и системы задач.
Рассмотрим элемент графовой
модели (см. рисунок 1).
Рисунок 1
Графовая модель
![]()
где 1, 2 и 3 – элементы знания, при этом будем говорить,
что элемент 3 опирается на элемент 2, а элемент 2 опирается на элемент 1; будем
говорить, что элемент 3 выводим из элемента 2, элемент 2 выводим из элемента 1.
В современной методике
практикуется рассмотрение задачи как системы. Согласно работе О.Б. Епишевой и
В.И. Крупич [44] задача как система представляет собой непустое множество
элементов, на котором определено (реализовано) заранее данное отношение - это
отношение выполняет роль основного отношения. В соответствии с этим подходом целесообразно
каждой задаче сопоставить непустой набор вершин графа – тех элементов знания,
которые составляют структуру данной задачи, т.е. знание которых требуется для
ее решения. Будем говорить в дальнейшем, что задача ассоциирована (связана) с
набором вершин графа и, соответственно, с каждой вершиной этого набора. И
наоборот, будем говорить, что набор вершин графа (и каждая вершина из этого
набора) ассоциирована с задачей. Количество вершин графа, с которыми
ассоциирована задача, назовем объемом задачи. Скажем, что система задач
ассоциирована с элементом знания, если хотя бы одна задача из входящих в
систему ассоциирована с данным элементом знания.
Если задача ассоциирована с
элементом знания X, опирающимся на данный элемент знания Y, то будем говорить,
что задача опирается на элемент знания Y. Будем говорить, что система задач
опирается на элемент знания, если хотя бы одна задача из входящих в систему
опирается на данный элемент знания.
Применительно к данному
примеру задачу, ассоциированную с
вершиной 2 . назовем опирающейся на элемент 1.
Расстояние между элементами
1 и 2 примем равным 1, расстояние между вершинами 3 и 1 примем равным 2.
Максимальное расстояние
между любыми двумя элементами знания,
ассоциированными с данной задачей, назовем диаметром задачи. Примеры графовых
моделей задач и систем задач приведены ниже:
Задача №504
«Является ли квадратным
уравнение 3,7·x![]() -5·х+1=0»
-5·х+1=0»
Эта задача ассоциирована с
вершиной 1, не опирается ни на одну вершину в рамках данной темы, объем задачи равен
1, диаметр равен 0.
Графовая модель данной
задачи будет иметь следующий вид (см. рисунок 2):
Рисунок 2
Графовая модель задачи №504
![]()
Задача № 509 а): «Найдите
корни уравнения 4·x![]() -9=0»
-9=0»
Эта задача ассоциирована с вершинами
6, 7, 9, опирается на вершину 1, объем задачи равен 3, диаметр равен 2, задача
связывает элементы знания 6, 7, 9, длина связи между 6 и 7, 7 и 9 равна 1,
между 6 и 9 равна 2.
Графовая модель данной
задачи будет иметь следующий вид (см. рисунок 3):
Рисунок 3
Графовая модель задачи №509
![]()
Задача:
«Решить уравнение x![]() (x
(x![]() -2·х+1)=0»
-2·х+1)=0»
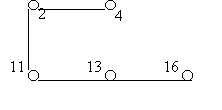
Эта задача ассоциирована с
вершинами 2, 4, 11, 13, 16, опирается
на вершину 1, объем задачи равен 5, диаметр равен 4.
Длина связи между 2 и 4, 2 и
11, 11 и 13, 13 и 16 равна 1, между 4 и 11, 2 и 13, 11 и 16 равна 2, между 4 и
13, 2 и 16 равна 3, между 4 и 16 равна 4.
Графовая модель данной
задачи будет иметь следующий вид (см. рисунок 4):
Рисунок 4
Графовая модель задачи
«Решить уравнение x![]() (x
(x![]() -2·х+1)=0»
-2·х+1)=0»
Рассмотрим систему задач,
состоящую из задач №№509 а) – г) (модели этих задач полностью совпадают с
моделью задачи №509 а), рассмотренной выше) и задачи «Решить уравнение x![]() (x
(x![]() -2·х+1)=0».
-2·х+1)=0».
Модель такой системы
изображена ниже (см. рисунок 5):
Рисунок 5
Графовая модель системы
задач
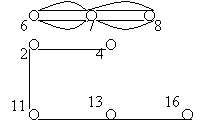
Данная система задач
связывает между собой элементы знания 2, 4, 11, 13, 16 и 6, 7, 8. Объем этой
системы равен 8. Длина связи между элементами знания 2 и 4 равна 1, между 6 и 8
равна 2, между 4 и 16 равна 4, между 6 и 2 равна ∞. Соответственно,
диаметр этой системы равен ∞.
Таким образом, согласно
введенным выше определениям, в рамках графовой модели задаче однозначно
сопоставляется подграф модели теоретического материала по данной теме,
вершинами которого являются все элементы знания, ассоциированные с данной задачей.
Очевидно, что решение задачи
требует владения всеми элементами
знания, ассоциированными с данной задачей. Кроме того, владение некоторым
элементом знания X невозможно без владения всеми элементами знания Y, на которые
он опирается (если речь не идет о формальном владении информацией).
Слабо ассоциированным с
данной задачей назовем каждый элемент знания, либо ассоциированный с данной
задачей, либо такой, что задача опирается на него.
Таким образом, решение
задачи требует знания всех элементов знания, слабо ассоциированных с ней. Ели
речь идет об упражнении, то его выполнение способствует отработке всех
элементов знания, слабо ассоциированных с этим упражнением (задачей) и связей
между ними.
Предложенные графовые модели
учебной задачи и системы задач позволяют, в частности, решить проблему
автоматизированного отбора оптимальных систем учебных заданий в соответствии
текущим уровнем обученности и образовательными запросами учащегося, что
позволяет реализовать идеи личностно ориентированного обучения в рамках информационного
образовательного пространства «средняя школа - вуз».
Литература
1. Епишева О.Б., Крупич В.И.
Учить школьников учиться математике: Формирование приемов учебной деятельности:
Книга для учителя. – М.: Просвещение, 1990. – 127 с.
The construction of model of
system of educational tasks by means of graph models
Boyarinov D. A.
In the article the
approach to the construction of graph models of systems of educational tasks is
stated.
Key
words: educational task, system of educational tasks,
graph model, diameter of an educational task.
Исследование выполнено при
финансовой поддержке РГНФ
Грант № 10-06-58605 а/Ц
Бояринов Дмитрий Анатольевич
кандидат педагогических наук
Смоленский Государственный Университет
доцент кафедры информатики
Смоленский
государственный университет
Кафедра
информатики
Поступила в редакцию
11.09.2011