Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 10. -

Вып. 3. - 2011. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-31-html/TITL-31.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-31-html/cont.htm

 

 

 

УДК 621.396.96

 

Об использовании алгебраического подхода для классификации объектов

 

Ó 2011 г. Волоткович Д. А., Макеенкова Т. Н.

 

 

(makeenkova.doc)

 

Итогом работы любого распознающего автомата является принятие решения о классе (типе) распознаваемого объекта. Поэтому одна из задач математического моделирования заключается в поиске оптимальной процедуры принятия решения. В статье рассмотрен алгебраический подход к решению этой задачи и сформулированы рекомендации применения алгоритмов распознавания исходя из объема имеющейся априорной и апостериорной информации.

 

Ключевые слова: система распознавания, алгоритмы распознавания, решающее правило, алфавит классов, вероятность распознавания.

 

 

Построение эффективных систем распознавания базируется в значительной мере на методах математического моделирования, сутью которых являются описания процессов распознавания на языке математики: формул, аналитических соотношений, уравнений, алгоритмов. Результатом описаний является построение комплекса математических моделей, представляющего собой инструмент для организации исследований, основанных на проведении целенаправленных математических экспериментов.

Основная цель математического моделирования систем распознавания состоит в том, чтобы оценить ее эффективность при найденном или заданном алфавите классов и предлагаемом в качестве рабочего словаре координатных и некоординатных признаков. Наиболее значимый критерий оценки эффективности системы распознавания – вероятность получения правильных решений при распознавании объектов, относящихся ко всем классам алфавита классов. Таким образом, критерий эффективности системы распознавания представляет собой функционал, зависящий от различных факторов, таких, как состав алфавита классов, меры достоверности априорного описания всех классов алфавита,  выбранный состав словаря признаков, ошибки их определения.

В общем виде функционал может быть записан следующим образом:

 

,

 

где  - алфавит классов;

 - словарь признаков;

 - ошибки определения признаков, ;

,  - ошибки априорного описания классов,  [1].

Для математического моделирования системы распознавания строится статистическая модель, которая реализует многократное повторение процесса распознавания объектов каждого класса. Множество случайных исходов решения задачи распознавания, полученное в ходе статистических испытаний, позволяет определять искомые оценки для вероятностей правильных и ошибочных решений и оценивать зависимость этих вероятностей от условий функционирования системы [1].

Для построения модели необходимы:

множество возможных решений, которые могут быть приняты системой управления на основании результатов распознавания неизвестных объектов или явлений ;

априорный словарь признаков ;

исходное множество объектов ;

значения выигрышей, получаемых системой управлений от конкретных решений из множества возможных решений , принимаемых по результатам решения задачи распознавания.

Исход принятия решения о классе наблюдаемого объекта в сильной степени зависит от алгоритма (правила) принятия решения. Поэтому одна из задач математического моделирования заключается в поиске оптимальной процедуры принятия решения.

Существуют различные алгоритмы распознавания: детерминированные (основанные на проведении в признаковом пространстве решающей границы), вероятностные (основанные на теории статистических решений), алгоритмы вычисления оценок, логические алгоритмы (базирующиеся на алгебре логики) и структурные (лингвистические) алгоритмы. В каждой конкретной ситуации необходимо выбирать наилучший алгоритм распознавания [2].

В последнее время широкое распространение получил алгебраический подход к построению алгоритмов распознавания, который заключается в следующем. Пусть некоторая задача распознавания решается с помощью конечного набора С решающих функций, например, С1 – линейная решающая функция, С2 – квадратичная, С3 – правило k ближайших соседей. Если качество полученных этими функциями решений окажется неудовлетворительным, то можно расширить множество используемых функций и среди этого расширенного множества найти функцию, которая давала бы более высокий результат. Можно выделить два типа расширений множества решающих функций. В первом случае некоторые параметры исходных функций из констант превращаются в переменные. Варьирование значениями этих переменных порождает широкий класс решающих функций различного типа. Во втором случае (если оптимального решения получить не удается) из набора простых правил С можно сконструировать с помощью алгебраических операторов более сложное правило для решения задачи распознавания [3].

Процедура отнесения неизвестного объекта, подлежащего распознаванию, к соответствующему классу может быть разделена на два этапа:

вычисление меры близости неизвестного объекта с каждым классом (в логических алгоритмах значения признаков неизвестного объекта подставляются в логические уравнения, описывающие классы);

в соответствии с выбранным порогом на основании информации, полученной на первом этапе, принимается окончательное решение о принадлежности неизвестного объекта к соответствующему классу [2].

Любой алгоритм распознавания в соответствии с этапами может быть представлен в виде двух последовательно выполняемых алгоритмов В и С. Алгоритм В переводит исходную информацию об объектах общим числом q в числовую матрицу размерности q × m, где m – число классов. Алгоритм С – «решающее правило» – переводит полученную матрицу в матрицу ответов, составленную из символов 1, 0, × (1 – объект относится к данному классу, 0 – объект не относится к данному классу, × – не установлено, относится объект к данному классу или не относится), имеющую ту же размерность.

При алгебраическом подходе алгоритм В называют распознающим оператором. С распознающими операторами можно производить операции сложения, умножения и умножения на число, позволяющие расширять их совокупность. Если в исходном семействе распознающих алгоритмов отсутствует алгоритм, правильно решающий задачу распознавания, то искомый, правильно решающий задачу распознавания алгоритм, в алгебраическом расширении существует и может быть записан в явном виде.

Рассмотрим формальную постановку этого подхода. Пусть дана исходная совокупность объектов , известны классы , к которым относятся эти объекты, а также группа неизвестных объектов, подлежащих распознаванию – . Любой из выбранных распознающих операторов, примененный к исходной совокупности объектов, позволяет получить информационную матрицу (матрицу ответов) вида

 

.

 

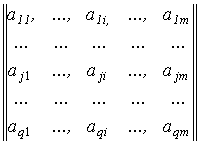Введем в рассмотрение произвольные фиксированные положительные числа d1 и d2 (пороги), при этом 0 < d1 < d2. Тогда с помощью алгоритма С матрица ответов может быть представлена в виде

 

 

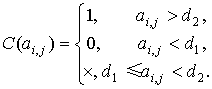
С помощью операций сложения, умножения (при перемножении распознающих операторов используется поэлементное перемножение соответствующих элементов матриц), умножения на число можно построить такой распознающий оператор, который позволяет правильно решать задачу распознавания. В общем виде распознающий оператор может быть записан в следующем виде

 

,

 

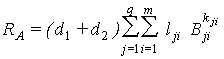где d1 и d2 – пороги,

 – константы,

 – распознающие операторы,

 – степень операторного многочлена (порядок алгебраического замыкания),  [4].

Применение разных распознающих алгоритмов к одной и той же задаче может приводить к получению различных информационных матриц. Поэтому возникает проблема построения корректирующих методов, которые позволяли бы вырабатывать единую матрицу ответов, сопоставляя информационные матрицы различных алгоритмов.

Рассмотренные решающие процедуры уместны для распознавания объектов отдельно взятым распознающим автоматом (РА), например, РА, установленным на РЛС обнаружения или сопровождения.

В случае коллектива распознающих автоматов целесообразно придерживаться другого подхода принятия окончательного по системе решения на основании информации, поступающей от разных РА. Решающее правило, которое может быть реализовано в этом случае, существенно зависит от того, какую информацию передают на пункт управления (ПУ) распознающие автоматы, а выходная информация РА определяется тем, какие функции они выполняют.

На практике часто встречается ситуация, которая состоит в совместной обработке результатов распознавания одной и той же цели разными распознающими автоматами. Тогда задача принятия окончательного (общего) решения о классе наблюдаемого объекта может быть решена путем анализа совокупности частных решений, сформированных разными РА.

В общем случае возможны и смешанные варианты, когда отдельные РА формируют частные решения о классе цели, а остальные выдают на схему принятия общих решений результаты измерения признаков или значения мер ее сходства с разными эталонами. Возможна также ситуация, когда у нескольких РА алфавиты распознаваемых ими классов не совпадают с алфавитом общих решений.

Если решение о классе воздушной цели принимается непосредственно на сопрягаемых с пунктом управления средствах обнаружения и по линиям связи одновременно с параметрами цели передается информация о ее классе, а также степень доверия, то в этом случае на ПУ происходит объединение полученных данных и решений.

Желательно, чтобы алфавит распознаваемых классов (подклассов, типов, свойств) воздушных объектов был для всех радиолокационных средств единым и составлен таким образом, чтобы он мог использоваться на каждом средстве с учетом возможных способов обработки информации распознавания как на этом, так и на сопрягаемых с ним средствах, в соответствии с их функциональным назначением, техническими характеристиками и решаемыми задачами.

В таком случае для решения о классе цели достаточно обобщать поступающую от разных РЛС информацию с учетом соответствующих мер доверия (вероятностей отнесения цели к одному из классов), либо организовать процедуру голосования.

При относительно низкой средней достоверности принимаемых решений для распознавания можно применять вероятностный подход. Для этого на пункте управления необходимо хранить в ПЗУ СЦВМ матрицы мер доверия каждому средству обнаружения и вероятности правильного распознавания целей ими (если они (вероятности) не поступают от РЛС). желательно, чтобы средняя вероятность правильного распознавания  при этом была на уровне не менее 0,75. Это требование  может быть ужесточено или, наоборот, ослаблено, в зависимости от характера решаемых на ПУ задач и сопрягаемых с ним типов РЛС и ЗРК. Решение о классе цели принимается согласно формуле Байеса:

 

,

 

где  ­– вероятность отнесения k-ой РЛС объекта Аi к i-му классу.

Для усиления принимаемых решений целесообразно учитывать информативность РЛС, т.е. ввести весовые коэффициенты  для каждой РЛС, характеризующие меру доверия источнику информации:

 

.

 

Например, для РЛС метрового диапазона можно установить коэффициент   = 0,2, для РЛС дециметрового диапазона – 0,3, а для модуля сантиметрового диапазона – 0,5. О конечных числовых значениях коэффициентов  можно  говорить только после проведения натурных экспериментов. Если же такой информации нет, то коэффициенты на начальном этапе могут быть приняты равными.

При распознавании объектов могут применяться и методы алгебры логики. Например, в тех случаях, когда существенны не только количественные соотношения между величинами, характеризующими рассматриваемые случайные процессы, но и связывающие их логические зависимости. Такое может быть, когда отсутствуют сведения о количественном распределении объектов по пространственным, временным, весовым, энергетическим или каким-нибудь другим интервалам в соответствующем пространстве признаков, а имеются лишь детерминированные логические связи между рассматриваемыми объектами и их признаками; или известны распределения объектов в пространстве признаков, законы распределения ошибок измерения величин, характеризующих отдельные объекты, но логические зависимости, связывающие признаки и классы объектов, сложны и не поддаются непосредственному анализу.

Для решения задач, в которых исходные данные являются ненадежными и слабо формализованными, можно применять аппарат нечетких множеств и нечеткой логики (при наличии неограниченных ресурсов вычислительных систем). В большинстве практических случаев на пунктах управления такими ресурсами не располагают, поэтому в настоящее время алгоритмы распознавания, основанные на нечеткой логике, не нашли широкого применения.

В заключение необходимо отметить, что выбор того или иного решающего правила или алгоритма – это процесс творческий. Он требует учета многих факторов, и предпочтение следует отдавать варианту, наиболее подходящему решаемой задаче.

 

литература

 

                    1.     Горелик А. Л. Селекция и распознавание на основе локационной информации. М., Радио и связь, 1990. С. 23, 25, 26

                    2.     Горелик А. Л., Скрипкин В. А. Методы распознавания. М., Высш. шк., 1984. С. 33, 186.

                    3.     Загоруйко Н. Г. Прикладные методы анализа данных и знаний. – Новосибирск: Изд-во Ин-та математики, 1999. С. 69–70.

                    4.    Журавлев Ю. И. Об алгебраическом подходе к решению задач распознавания или классификации. – Проблемы кибернетики. М.: Наука, 1978, вып. 33.

 

 

ABOUT USE THE ALGEBRAIC APPROACH FOR CATEGORIZATION OBJECT

 

Volotkovich D., Makeenkova T.

 

The result of the work of any recognizing automation is a decision making about the class (the type) of a recognition object. So one of the problems of mathematical modeling is searching for optimal procedure for decision making. Algebraic approach to decision of this problem is considered in the article and the recommendations to the using of algorithm recognitions are formulated coming from volume of available a priori and a posteriori information.

Key words: recognition system, recognition algorithms, desicion rule, alphabet of the classes, probability of the recognition.

 

 Военная академия войсковой ПВО

Вооруженных Сил Российской Федерации

 имени Маршала Советского Союза А.М. Василевского

(ВА ВПВО ВС РФ)

Поступила в редакцию 02.06.2011.