Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 10. -

Вып. 3. - 2011. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-31-html/TITL-31.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-31-html/cont.htm

 

УДК 681.3.06

 

МОДЕЛЬ РАСЧЁТА ПАРАМЕТРОВ ОПЕРАТИВНОГО ВОССТАНОВЛЕНИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ РЕАЛЬНОГО ВРЕМЕНИ

 

Ó 2011 г. Волосенков В. О. 

 

(volosenkov.doc)

 

Рассматривается задача  расчёта параметров оперативного восстановления вычислительных систем реального времени. Предлагается математическая модель для расчёта  параметров оперативного восстановления вычислительных систем реального времени при допустимом уровне деградации.

Ключевые слова: вычислительная система, надёжность, отказ, восстановление.

 

Центральной проблемой проектирования вычислительных систем реального времени является проблема обеспечения надёжности. Одним из факторов, определяющих надёжность функционирования вычислительных систем реального времени являются ошибки в программах [1, 2]. Программное обеспечение (ПО) вычислительных систем, функционирующих в режиме реального времени, характеризуется боль­шим количеством программных модулей, обеспечивающих преобразование информации ограниченным количеством выполняемых функций, повышенными требовани­ями к времени выполнения и надежности обрабатываемой информации [3, 4]. Быстрое реагирование на искажения программ или данных и восстановление работоспособности за вре­мя, меньшее, чем порог между сбоем и отказом, позволяет обес­печить высокую надежность вычислительной системы. Поэтому проблема оценки параметров оперативного восстановления вычислительных систем реального времени, является достаточно сложной и актуальной в современных условиях. Одним из путей решения данной проблемы является предлагаемая модель определения параметров оперативного восстановления вычислительных систем реального времени, позволяющая учитывать влияние ошибок в программном обеспечении.  

Известно [5], что для восстанавливаемых систем средняя наработка на отказ T0 определяется следующим выражением:

,

(1)

где P(t) – условная вероятность безотказной работы вычислительной  системы, при условии, что в начальный момент времени все ее элементы работоспособны.

Для определения условной вероятности безотказной работы рассмотрим систему, состоящую из N модулей, в том числе количество модулей универсальных программируемых контроллеров – Nk.

Анализ надежности проводим при следующих предположениях:

все модули вычислительной системы сопоставимы по сложности и имеют одинаковую вероятность безотказной работы, равную Pm(t);

во время функционирования вычислительной системы в неиспользуемых в текущий момент модулях универсальных программируемых контроллерах производится оперативное тестирование, позволяющее обнаружить ошибки ПО с вероятностью α;

вероятность одновременного отказа двух или более программных модулей пренебрежимо мала по сравнению с вероятностью отказа одного модуля;

при обнаружении неисправного модуля производится автоматическое восстановление работоспособности вычислительной системы перераспределением ресурсов, в результате отказавший модуль универсального программируемого контроллера отключается, а его функции распределяются между оставшимися исправными модулями;

для проведения оперативного тестирования и перераспределения ресурсов используется резерв времени. Эти процедуры занимают время, равное tав и осуществляются до достижения предельно допустимого количества отключенных модулей M;

за время проведения оперативного тестирования и перераспределения ресурсов отказы в модулях не возникают.

При выдвинутых предположениях все возможные с точки зрения работоспособности состояния вычислительной системы можно сгруппировать в следующие подмножества в зависимости от модуля, в котором возник отказ.

Подмножество 0. Оно включающее в себя единственное состояние, при котором все элементы вычислительной системы работоспособны.

Подмножество 1. К нему относятся все состояния вычислительной системы, при которых очередной отказ возник в одном из модулей универсального программируемого контроллера, не используемом в текущий момент времени, предыдущие отказы, возникшие в этих модулях, изолированы реконфигурацией.

Подмножество 2. В это подмножество входят состояния вычислительной системы, характеризующиеся тем, что очередной отказ возник в используемом модуле универсального программируемого контроллера, предыдущие отказы, возникшие в этих модулях, изолированы реконфигурацией.

Подмножество 3. Оно включает состояния, при которых отказавшие модули универсальных программируемых контроллеров отключены, оставшиеся модули исправны.

Подмножество 4. В него входят состояния, при которых отказ произошел в любом модуле, кроме модулей универсального программируемого контроллера при наличии резерва времени на реконфигурацию, либо отказ произошел в системе после достижения предельного уровня деградации.

Граф переходов вычислительной системы между указанными подмножествами состояний в процессе функционирования представлен на рисунке 1.

В начальный момент времени все модули вычислительной системы исправны, и она находится в состоянии 0.

При возникновении отказа он может распределиться по модулям вычислительной системы следующим образом.

Отказ произошел в любом из модулей, за исключением модулей универсальных программируемых контроллеров. В этом случае система перейдет в неработоспособное состояние 3M+1 и будет находиться в нем до окончания ремонта.

Отказ произошел в одном из используемых в текущий момент универсальных программируемых контроллеров – произойдет переход вычислительной системы в неработоспособное состояние 2M+1, в котором она будет находиться до окончания времени, выделенного контроллеру на обслуживание прерывания. По истечении этого времени контроллер будет освобожден и система перейдет в состояние M+1.

Отказ произошел в неиспользуемом в текущий момент универсальном программируемом контроллере, тогда вычислительная система перейдет в состояние M+1 и сохранит работоспособность. В этом состоянии она будет находиться до тех пор, пока отказ не будет обнаружен средствами оперативного тестирования, после чего неисправный контроллер будет отключен и его нагрузка распределена между исправными контроллерами, в результате чего система перейдет в состояние 1. Если отказ контроллера не обнаруживается средствами оперативного тестирования, то при поступлении в систему прерывания, обслуживаемого этим контроллером, она перейдет в состояние 2M+1.

 

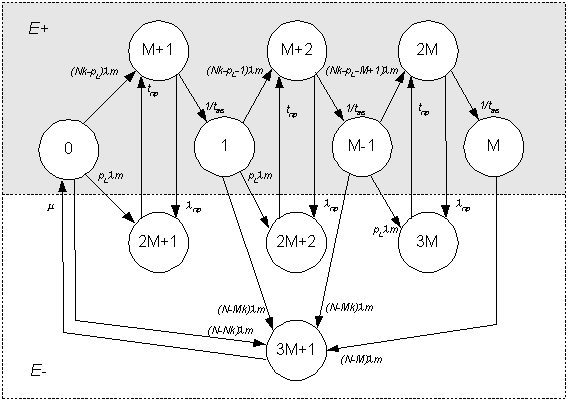
Рисунок 1 – Граф состояний вычислительной системы:

 

lm – интенсивность отказов модуля вычислительной системы;

lпр – интенсивность поступления прерываний абонентов;

tпр – среднее время обработки прерываний;

tав – среднее время восстановления;

N – число модулей вычислительной системы;

M – допустимое число отказавших модулей вычислительной системы;

rS  – средний суммарный коэффициент загрузки универсальных программируемых контроллеров;

m – интенсивность восстановления вычислительной системы.

 

Попав в состояние 1, вычислительная система будет находиться в нем до появления следующего отказа. При его возникновении возможные переходы из состояния 1 в состояния 3M+1, 2M+2, M+2 будут определяться теми же условиями, что и для состояния 0.

По мере накопления отказов, вычислительная система попадет в состояние M, характеризующееся невозможностью дальнейшего перераспределения ресурсов из-за достижения предельного уровня деградации, вызванного исчерпанием резерва времени. Возникновение любого отказа в этом состоянии переведет вычислительную систему в неработоспособное состояние 3M+1.

На приведенном графе (рисунок 1) выделим множество работоспособных состояний E+. К множеству работоспособных состояний относятся либо состояния, в которых вычислительная система не содержит отказов (состояние 0, подмножество 0), либо отказы существуют, но не нарушают ее работоспособность из-за того что они произошли в неиспользуемых в текущий момент модулях универсальных программируемых контроллерах (состояния M+1 ÷ 2M, подмножество 1) или были обнаружены с помощью оперативного тестирования и изолированы реконфигурацией (состояния 1 ÷ M, подмножество 3). Остальные состояния относятся к неработоспособным, так как попадание в них приводит к устойчивой потере работоспособности (состояние 3M+1, подмножество 4), либо к появлению ошибок в процессе функционирования (состояния 2M+1 ÷ 3M, подмножество 2).

Будем считать, что система работоспособна до тех пор, пока состояния, по которым она перемещается в процессе функционирования, принадлежат множеству E+. Попадание, хотя бы однократное, в какое либо из состояний множества E- переводит вычислительную систему в неработоспособное состояние.

В этом случае вычислительная система сохранит работоспособность в течении времени (0,t) если за это время не произойдет ни одного отказа, либо после возникновения первого и последующих отказов они произойдут в модулях универсальных программируемых контроллеров, неиспользуемых в текущий момент времени, и резерв времени будет достаточен для их обнаружения средствами оперативного тестирования и проведения реконфигурации.

Вероятность того, что в вычислительной системе, при принятом допущении о равной надежности ее модулей за время (0,t) не произойдет ни одного отказа, определяется выражением:

,                                                 (2)

где Pm(t) – вероятность безотказной работы одного модуля вычислительной системы; N – число модулей в составе вычислительной системы.

 При допустимом уровне деградации M = 1 в течение времени (0,t) при следующих возможных событиях:

за время работы в течение рассматриваемого интервала времени (0,t) в рассматриваемой системе не произойдет ни одного отказа;

произойдет отказ в незадействованном модуле универсального программируемого контроллера вычислительной системы в произвольный момент времени τ<t, отказ будет обнаружен средствами оперативного тестирования и реконфигурация будет проведена до окончания резерва времени, а оставшиеся модули безотказно отработают до конца интервала (0,t).

Вероятность безотказной работы вычислительной системы на интервале времени (0,t) в этом случае будет определяться выражением:

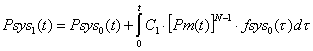,                     (3)

где C1 – вероятность того, что первый отказ обнаружен и восстановление вычислительной системы проведено до окончания резерва времени;  – вероятность того, что оставшиеся модули не откажут до момента времени t; τ – время возникновения отказа; fsys0(τ) – плотность распределения наработки до отказа вычислительной системы, определяемая, как:

                .                                           (4)

Проведя аналогичные рассуждения, получим выражение для вероятности безотказной работы вычислительной системы после возникновения очередного i-го отказа в интервале времени (0,t):

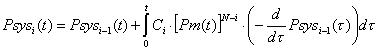,                 (5)

где Ci –вероятность того, что очередной i-й отказ обнаружен и восстановление вычислительной системы проведено до окончания резерва времени.

Для определения коэффициента Ci представим его в виде:

,                                            (6)

где α – вероятность отказа модулей вычислительной системы с учётом влияния ошибок ПО; Ci,1 – вероятность того, что отказ произойдет в неиспользуемом модуле;  Ci,2 – вероятность того, что в течение резервного времени отказ будет обнаружен и произведено восстановление вычислительной системы.

Вероятность того, что очередной i-й отказ произойдет в неиспользуемом модуле, определяется как:

,                                          (7)

где  – минимальное целое значение, превосходящее ;  – суммарный коэффициент загрузки каналов.

При экспоненциальном распределении времени, необходимого для обнаружения отказа и восстановления tав, коэффициент Сi,2 будет равен:

,                                            (8)

где  – средняя величина резерва времени до проведения i‑го восстановления.

Из формул (6), (7), (8) получим выражение для определения коэффициента Ci:

,                        (9)

Рекуррентная формула (5), с учетом выражения (9) позволяет определить условную вероятность безотказной работы вычислительной системы при допустимом уровне деградации M как:

.                  (10)

Из выражения (10) получим среднее время наработки на отказ с учётом влияния ошибок ПО:

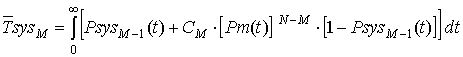. (11)

Полученные выражения (10), (11) выражают зависимость вероятности безотказной работы и средней наработки до отказа от величины вероятности отказа модулей вычислительной системы с учётом влияния ошибок программного обеспечения α, предельно допустимого уровня деградации M, времени, необходимого на проведение автоматического восстановления работоспособности tав и величины резерва времени tрез.

 

Литература

 

1. Липаев В. В. Системное проектирование сложных программных средств для информационных систем. М., СИНТЕГ, 1999. 257 с.

2. Липаев В. В. Отладка сложных программ. М., Энергоатомиздат, 1993. 235 с.

3. Липаев В. В. Надежность программных средств. М., СИНТЕГ, 1998. 240 с.

4. Дружинин В. Г. Надёжность автоматизированных систем. М., Энергоатомиздат, 1986. 536 с.

5. Черкесов Г. Н. Надёжность программно-аппаратных комплексов. СПб., Питер, 2005. 479 с.

 

MODEL OF CALCULATION OF PARAMETERS OF OPERATIVE RESTORATION OF COMPUTING SYSTEMS OF REAL TIME 

 

Volosenkov V.O.

 

The problem of calculation of parametres of operative restoration of computing systems of real time is considered. The mathematical model for calculation of parametres of operative restoration of computing systems of real time Is offered at admissible level of degradation.

Key words: the computing system, reliability, refusal, restoration.

 

Военная академия войсковой ПВО Вооруженных Сил Российской Федерации

 имени Маршала Советского Союза А.М. Василевского

(ВА ВПВО ВС РФ)

Поступила в редакцию 20.03.2011.
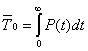