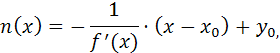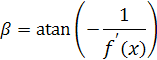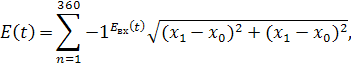Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 10. -

Вып. 3. - 2011. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-31-html/TITL-31.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-31-html/cont.htm

УДК 621.396.61(075)

СПОСОБ РАСЧЕТА И ОПТИМИЗАЦИИ СВЕРХШИРОКОПОЛОСНОГО ПЕЧАТНОГО ИЗЛУЧАТЕЛЯ

Ó 2011 г. Земцов А. В., Битаев Е. С., Амозов E. В.

(zemtsov.doc)

Современная элементная база позволяет создавать генераторы с длительностью импульса в единицы и доли наносекунд, что ведет к созданию сверхширокополосных систем в основе которых лежат сверхширокополосные приемники и передатчики. Однако, в связи с тем, что электромагнитное поле создаваемое сигналами сверхкороткой формы не является стационарным что делает невозможным расчеты антенных устройств традиционными способами.

Ключевые слова: сверхширокополосный излучатель, печатная антенна, оптимизация антенны.

Печатные антенны берут своё начало от использования в СВЧ устройствах таких изделий как микрополоски, щелевые линии и копланарные линии. Факт излучения таких линий был обнаружен в 50х годах прошлого столетия, однако первое практическое применение они получили в 70х. Такие антенны реализуются по технологии печатных плат, что сопутствует общей концепции минимизации электронных устройств. Известны различные способы классификации печатных антенн, но наиболее применяются классификация по геометрическому виду излучающего элемента антенны и по способу питания этого элемента. Независимо от этой классификации печатные антенны обладают рядом преимуществ:

легкий вес и небольшие размеры;

простое изготовление по технологии печатных плат;

упрощенная интеграция с электронными компонентами (размещение СВЧ устройств с обычными компонентами на одной плате);

возможность изготовления антенны на изогнутой плоскости что позволяет «вписать» антенну в агрегат носитель;

упрощенное создание антенных решеток.

Однако, существуют и недостатки:

относительно узкая рабочая полоса частот;

некоторые эффекты, ведущие к снижению качества работы антенны, такие как, потери в диэлектрике, появление поверхностных волн в месте соприкосновения диэлектрика и воздуха;

сложности в согласовании линии и антенны.

Печатные антенны в основном ведут себя как резонаторы, это ведет к достаточно узкой полосе рабочих частот, наиболее часто несколько процентов. Однако, существуют печатные антенны имеющие более широкую полосу.

Самый простой вид такой антенны – патч антенна (от англ. Path – путь). Форма излучателя такой антенны может иметь один из видов, показанных на рисунке 1.

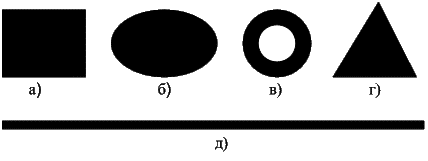
Рисунок 1 – Внешний вид излучателей (а) прямоугольный (квадратный);

б) эллиптический (круглый); в) кольцо; г) треугольный; д) диполь

Излучающие элементы могут быть запитаны непосредственно от линии передачи или через электромагнитную связь без соединения с передающей линией, при условии их ближайшего расположения.

Ниже приведены наиболее используемые методы для расчета печатных антенн:

метод линии передачи, в котором прямоугольная печатная антенна представлена как участок микрополосковой линии, излучающий своими краями;

метод полости, в котором расстояние между излучателем и пластиной заземления описывается как резонансная электромагнитная полость которая протекает (а следовательно и излучает) сквозь горизонтальную плоскость;

метод моментов, используемый для решения двумерного интегрального преобразования, которое вводит функцию Грина в геометрию плоскости и позволяет расширить её для многослойных структур.

Основной недостаток этих методов заключаются в том, что каждый расчет поля идет для одной конкретной частоты. Чтобы рассчитать широкий диапазон значений, необходимо считать поле на каждой частоте. Так же данные методы неприменимы для сигналов с широким спектром.

Расчет электрического поля круглого излучателя для точки питания расположенной в центре окружности

Решением данной проблемы являются дорогостоящие и ресурсоемкие пакеты проектирования СВЧ структур. Лидирующими являются Microwave Studio от CST и HFSS от Ansoft. Данные пакеты используют технологию «конечных элементов», в которой объем разбивается на ячейки, решается задача нахождения поля для каждой ячейки и затем результаты складываются. Данные пакеты включают в себя параметрическую оптимизацию и дают неплохие результаты, которые подтверждаются на практике.

Несмотря на все преимущества, данные программы обладают недостатками:

высокая стоимость (порядка десятков тысяч евро);

высокая требовательность к вычислительным ресурсам, что особенно актуально при расчетах сложных и больших по геометрии структур, а также при использовании оптимизации.

В данной статье рассматривается вариант применения такого пакета без существенных экономических затрат.

Предлагается создать упрощенную модель поля для излучателя, изображенного на рисунке 2 и произвести его оптимизацию. Затем, на основе полученных результатов уточнить модель с использованием CST MWS.

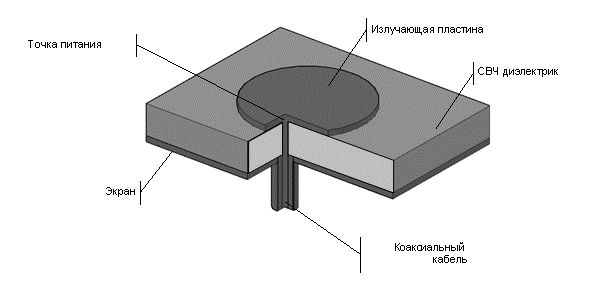
Рисунок 2 – Печатная антенна

Конструктивно рассматриваемая печатная антенна состоит из печатного излучателя на СВЧ диэлектрике к которому через питающий стержень подключен коаксиальный кабель источника сигнала. На рисунке 3 показан вид силовых линий напряженности поля круглой пластины.

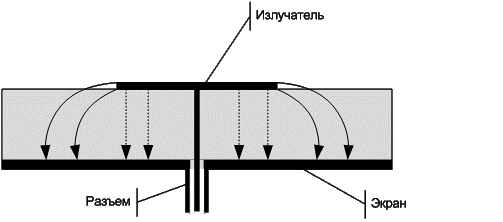
Рисунок 3 – Линии напряженности электрического поля печатной антенны

При толщине пластины стремящейся к нулю влияние эффекта искривления линий будет снижаться и силовые линии на краях по контуру пластины будут иметь значительные участки, вдоль которых кривизна линии минимальна. На рисунке 4 данный участок обозначен вектором . Рассматривая эти линий можно судить о характере поля создаваемого излучателем, а складывая вектора по периметру можно оценить поле. Анализа этого поля достаточно для оценки работы излучателя.

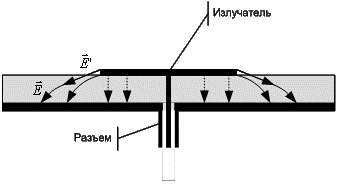
Рисунок 4 – Линии напряженности электрического поля заряженной пластины при толщине подложке, стремящейся к минимальной

Рассмотрим сложение векторов в точке наблюдения М(x,y), которая находится точно над центром излучателя.

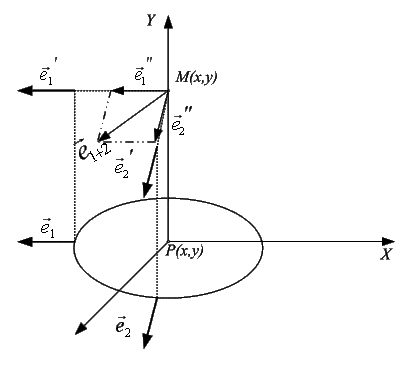
Рисунок 5 – Сложение двух векторов в точке наблюдения

Для того чтобы сложить вектора a и b в точке наблюдения необходимо методом параллельного переноса перенести их в точку наблюдения и сложить по правилу параллелограмма как показано на рисунке 5. Данную задачу удобно решать в координатном виде. Рассмотрим случай, когда точка питания располагается в центре окружности. Для решения этой задачи необходимо рассчитать координаты начал и окончаний всех векторов по контуру пластины. Рассмотрим расчет координат одного вектора. В прямоугольной системе координат расположим окружность радиуса R так, что начало системы координат совпадает с центром окружности. Проведем вектор, перпендикулярный касательной к окружности в произвольной точке окружности и обозначим координаты начала вектора X₀,Y₀ и координаты конца вектора X₁,Y₁

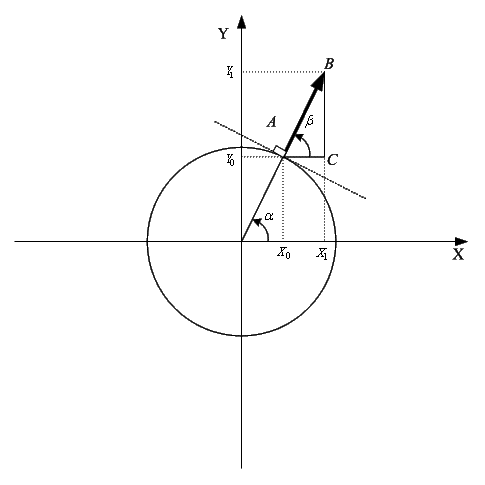
Рисунок 6 – Построения для расчета координат вектора

Чтобы найти координаты вектора необходимо знать точку начала вектора А(х,y), направление β и само значение вектора. Начальные точки векторов находятся из функции задающей контур излучателя. В данном случаи излучатель круглый, и формула задающая его контур – уравнение окружности (1)

(1)

Чтобы определить направление вектора необходимо найти производную функции (1), это дает коэффициент наклона касательной к точке окружности, а обратная величина – коэффициент наклона нормали. Таким образом, уравнение нормали будет иметь вид (2)

(2)

Г где

–

производная функции, задающей контур излучателя.

Используя формулу (3) находим угол наклона нормали к оси Х. В данном случае, когда контур – окружность, он будет равен α, но для других случаев он будет отличаться. Зная угол наклона нормали через формулу (3) можно найти значение координаты конца вектора (4)(5), где задается как модуль входного сигнала.

	(3)
	(4)
	(5)
	(6)

Имея аналитические выражения для поиска координат вектора можно вычислить значение этого вектора по формуле (6).

Расчет электрического поля круглого излучателя при его питании в точке, отличающейся от центра окружности

Рассмотрим случай, в котором питание излучателя осуществляется в точке, расположенной не в центре пластины.

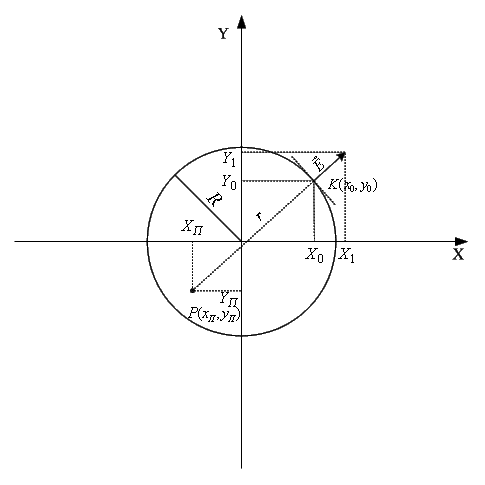
Рисунок 7 – Расположение точки питания печатного излучателя

На рисунке 7 показано расположение точки питания P(). Данная точка расположена на удалении от точки K(x₀,y₀) – начала текущего рассчитываемого вектора Е на расстояние r. Принимая во внимание данные обозначения, выразим время задержки :

(7)

где	c–скорость света.

Данное время задержки необходимо электромагнитной энергии чтобы пройти расстояние от точки питания к рассматриваемой точке края пластины. Объединяя формулы (1) – (7) можно получить итоговое выражение для вычисления напряженности поля в зависимости от времени:

(8)

где		–	формула, задающая контур пластины, выражение (1);
		–	зависимость входного сигнала от времени;
		–	координата точки окончания вектора по оси х;
		–	координата точки окончания вектора по оси y;
		–	координата х начала вектора на n направлении;
		–	координата y начала вектора на n направлении.

Немаловажными являются параметры входного сигнала . Этот сигнал должен соответствовать характеристикам рассчитываемого излучателя, максимальное значение амплитуды амплитудно-частотного спектра должно быть расположено в центре диапазона рабочих частот антенны.

Данным требованиям удовлетворяет сигнал (9).

(9)

где		–	максимальная амплитуда напряженности;
		–	период повторения функции заполнения;
	τ	–	период.

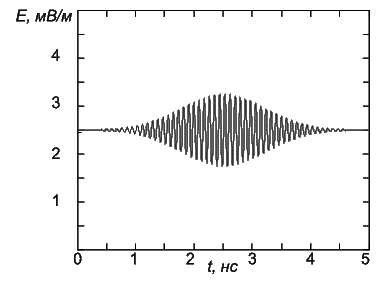
Рисунок 9 – Зависимость напряженности от времени

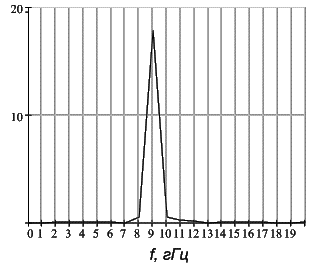
Рисунок 10 – Амплитудно-частотный спектр

Применяя выражения (1) – (9) можно составить алгоритм расчета суммарного вектора, данный алгоритм представлен на рисунке 10

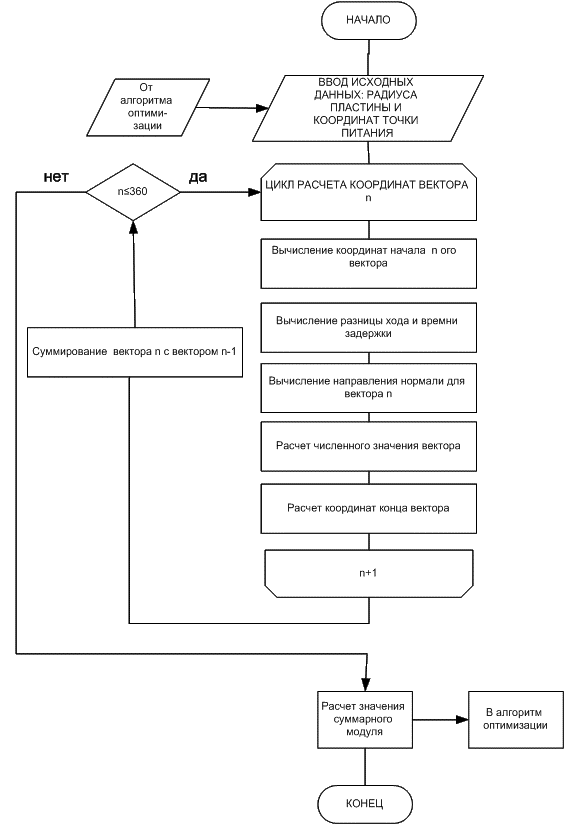
Рисунок 10 – Алгоритм расчета суммы векторов

Оптимизация положения точки питания

Для оптимизации точки питания используется сеточный алгоритм. Суть алгоритма заключается в делении всего пространства допустимых значений на сетку. Первые возможные значения выбираются случайно, далее идет анализ по 4 направлениям, этот этап показан на рисунке 11.

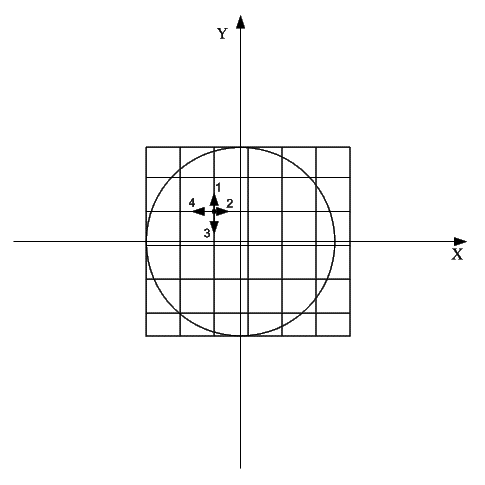
Рисунок 11 – Первый этап оптимизации.

В результате первых 4 расчетов полученные значения откладываются на сетке и точка питания сдвигается в сторону больших значений. В данном случаи в сторону значений 3 и 4, сетка к следующим 4 просчетам уточняется. Итерации повторяются до тех пор пока не будет достигнуто оптимальное значение при заданной точности (минимальные заданные размеры клетки сетки). На рисунке 12 показана вторая итерация с уточненной сеткой.

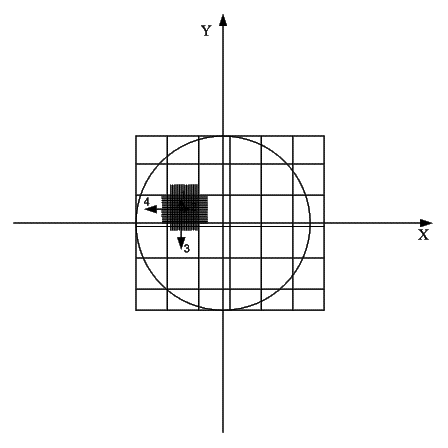
Рисунок 12 – Вторая итерация

Согласно алгоритма, показанного на рисунке 10 была написана программа на языке Delphi. Скриншот программы показан на рисунке 13.

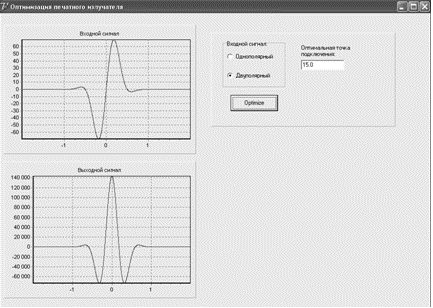
Рисунок 13 – Внешний вид программы

По результатам расчетов были построены проекции Е поля на плоскость антенны

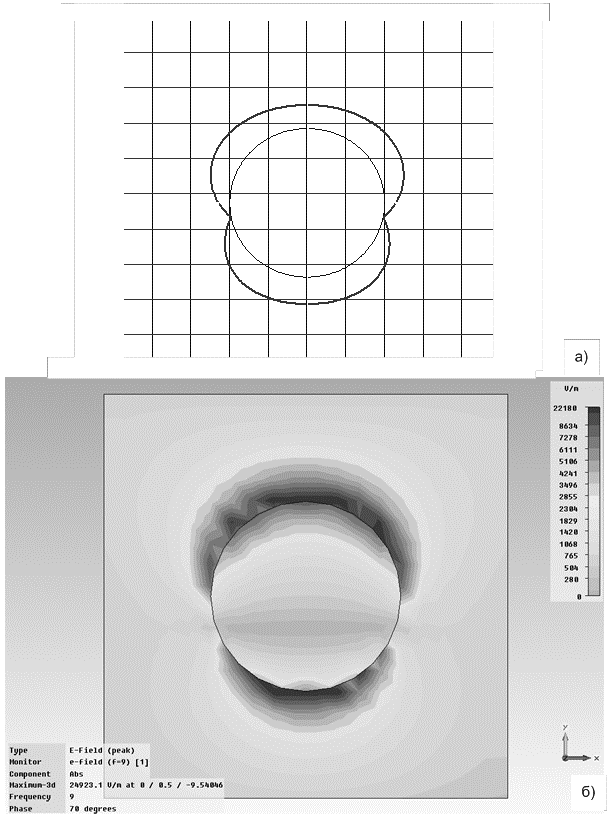
Рисунок 14 – Проекции электрического поля круглого излучателя, полученный при помощи модели (а) и в среде проектирования CST MWS (б)

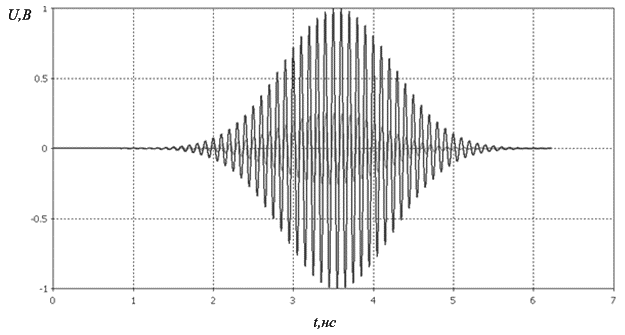
Рисунок 15 – Зависимость КСВ излучателя от частоты

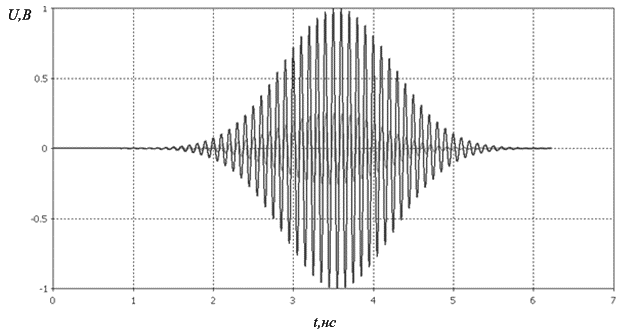
Рисунок 16 – Входной сигнал

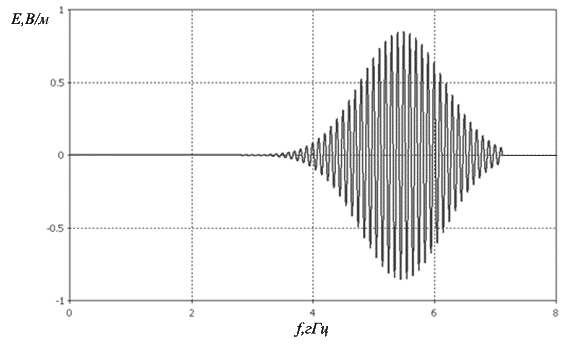
Рисунок 17 – Сигнал в пространстве

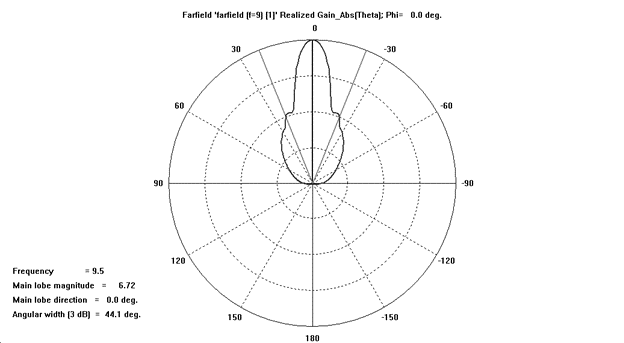
Рисунок 18 – Диаграмма направленности при φ=0°

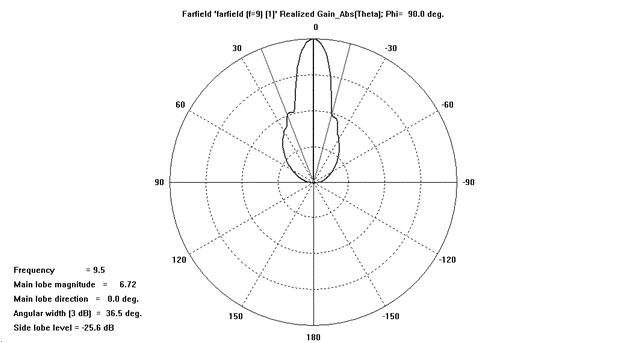
Рисунок 19 – Диаграмма направленности при φ=90°

В результате моделирования был получены размеры проектируемого печатного излучателя, удовлетворяющего требованиям рабочего диапазона, характеристики направленности и коэффициента усиления. При помощи предлагаемого алгоритма были уменьшены время разработки и оптимизации.

литература

1. Шахгильдян В. В., Власов В. А., Козырев В. Б. и др. Проектирование радиопередающих устройств. М., Радио и связь, 1993. 512 с.

2. Нефёдов Е. И. Устройства СВЧ и антенны. М., «Академия», 2009. 384 с.

METHOD OF CALCULATION AND OPTIMIZATION OF 

ULTRAWIDEBAND PRINTED-CIRCUIT ANTENNA

Zemtsov A., Bitaev E., Amozov E.

The modern element base allows you to create generators with a pulse duration in units and fractions of a nanosecond, which leads to the creation of ultrawideband systems which are based on ultrawideband receivers and transmitters. However, due to the fact that the electromagnetic field generated by the signal- form is not fixed which makes it impossible calculations of antenna devices in traditional ways.

Key words: ultrawideband emitter circuit antenna, antenna optimization.

Военная академия войсковой ПВО Вооруженных Сил Российской Федерации

 имени Маршала Советского Союза А.М. Василевского

(ВА ВПВО ВС РФ)

Поступила в редакцию 20.03.2011.