Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 10. -
Вып. 4. - 2011. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-32-html/TITL-32.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-32-html/cont.htm
УДК
536.3
ОБ ОШИБКЕ В
ТЕОРИИ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
Ó 2011 г. Конов А.Ф.
Приводятся примеры противоречий, наблюдаемые в
теории теплового излучения. Устранение противоречий позволяет установить, что
равновесная плотность энергии теплового излучения в замкнутой полости в 
раз превышает плотность энергии в потоке излучения. Формула,
по которой вычисляется равновесная плотность энергии в замкнутой полости,
получена на основе боровской теории водородного атома..Получено соотношение,
которое связывает термодинамическую шкалу Кельвина с законами теплового излучения.
Ключевые слова: тепловое излучение, длина
волны, максимум спектра излучения, формула Планка, закон смещения Вина,
давление излучения в замкнутой полости.
История развития теории теплового излучения, венцом которой стала формула Планка, указывает на то, что роль атома исключена из процесса преобразования тепловой энергии в энергию электромагнитного излучения.
Действительно, в результате интегрирования формулы Планка получается выражение (1).
(1)
где 
- постоянная Больцмана; 
- постоянная Планка; 
– скорость света.
В этом равенстве нет ни одного параметра, который указывал бы на то, что возникновение теплового излучения связано с физическими свойствами атома.
Описание спектра и плотности теплового излучения без учета физических свойств атома вызывает сомнение в том, что современная теория адекватно отражает тепловое излучение как физическое явление. Эти сомнения усиливаются существующими противоречиями в обсуждаемой теории. Некоторые из этих противоречий приводятся здесь для примера.
Одно из противоречий связано
с формулой (1). Если формулу (1) умножить и разделить на множитель 
: где 
- длина волны, соответствующая максимуму плотности излучения,
то получим выражение
.
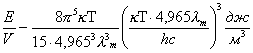(2)
Множитель в скобках равен единице, поскольку это
одна из форм записи закона смещения Вина.
В результате преобразования
формула (1) приобретает вид
. (3)
Из последней формулы следует, что плотность излучения прямо пропорциональна температуре излучающего тела и обратно пропорциональна кубу длины волны в максимуме плотности излучения.
Из формулы (3) следует, что
для введения множителя с размерностью 
нет физического обоснования.
Заменив
в формуле (3) длину волны, как
, запишем
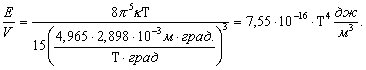(4)
Из
формулы (4) видно, что размерность «град.» сокращается в скобках знаменателя,
поэтому для удобства
можно перенести в числитель.
Другой
пример из ряда противоречий.
Постоянная
Стефана-Больцмана первоначально была определена экспериментально. Численное
значение постоянной и ее размерность записывается как
.
(5)
Последующие
усилия исследователей были направлены на то чтобы получить аналитическое
выражение константы, не обращая внимание на то, что постоянная 
не
отражает тех процессов, которые происходят при тепловом излучении.
Действительно,
тепловое излучение сопровождается двумя процессами. Один из процессов связан с
выносом энергии излучения из полости, другой – с расширением обьема фотонного
газа, при этом оба процесса происходят одновременно.
В
постоянной Стефана-Больцмана отражен только один процесс – вынос энергии излучения
и не отмечен процесс расширения фотонного газа.
Для
того чтобы привести в согласие размерность постоянной σ с процессами излучения эту константу необходимо разделить на с/4 (где с
– скорость света), а затем умножить на 
. Выполнив эти действия, запишем
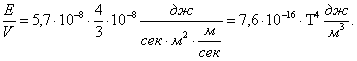(6)
В этом
выражении, как и в (4) 
не имеет размерности.
Формула (6) позволяет определить энергию излучения в 1
светового столбика, основание которого равно 1
, а его высота равна пути, пройденного светом за 1 секунду.
Размерности
формул (1), (3) и (6) одинаковые, а их численные значения равны между собой.
Все формулы описывают плотность излучения в световом потоке.
Далее
целесообразно привести пример противоречий, которые можно отметить при
согласовании основных положений теории теплового излучения с законами
термодинамики.
Как известно,
при адиабатическом сжатии или расширении фотонного газа, его энтропия
определяется соотношением 
/2/. Заменив в этом равенстве объём как 
, запишем 
. Извлекая из последнего выражения кубический корень, получим
. В теории теплового
излучения известны две константы, с размерностью «
», одна из них отражает закон сохранения и превращения
энергии 
. Другая является
законом смещения Вина 
. Здесь 
- длина волны в
максимуме спектра теплового излучения.
В
термодинамике адиабатическое сжатие увеличивает число частиц на единицу объема,
что приводит к увеличению давления. В тепловом излучении сжатие не изменяет
давление в замкнутой полости.
В
термодинамике размерность энтропии 
, а в тепловом излучении ее размерность 
.Трудно согласиться, что это одна и та же величина.
Таким
образом, теория излучения входит в противоречие с законами термодинамики.
В атомной теории Бора механизм излучения свободным атомом включает в себя все его физические свойства. Это указывает на то, что тепловое излучение и излучение свободным атомом должны иметь общую физическую основу.
Далее рассмотрим
процесс излучения стенкой в пустое пространство. В таком излучении излученная
энергия не возвращается на излучающую поверхность и, кроме того, на эту стенку
не падает излучение от других источников.
Согласно
экспериментальным данным радиационная температура ниже действительной
температуры тела. Это означает, что между излучающей поверхностью и внутренней
частью тела возникает температурный градиент. Отсюда следует, что отвод тепла
путем излучения производится со скоростью света, а подвод его к излучающей
поверхности определяется температурным градиентом и коэффициентом
теплопроводности вещества.
На
атомном уровне процесс преобразования тепловой энергии в энергию излучения
сводится к тому, что фонон при выходе на поверхность твердого тела подвергает
граничный атом сжатию. При этом кинетическая энергия фонона преобразуется в
потенциальную энергию атома. Последующий переход, которого из сжатого состояния
в состояние, разрешённое объемом ячейки твердого тела, сопровождается
электромагнитным излучением.
Процесс
излучения внутренней поверхностью полости, в которой установлен полный вакуум,
отличается от излучения поверхностью в пустое пространство тем, что излучение
граничным атомом в полость будет происходить до тех пор, пока давление фононного
газа со стороны твердого тела на излучающий атом будет равно давлению фотонного
газа со стороны полости. При достижении этого равенства граничный атом не излучает
и не поглощает энергии. При таких условиях в замкнутой полости достигается
равновесная плотность теплового
излучения. При этом в поверхностном слое вещества исчезает температурный
градиент, а граничный атом находится в таких же условиях, как и атомы внутри тела.
Экспериментально
определение равновесной плотности и спектрального состава теплового излучения
производится путём измерения суммарной энергии светового потока, выходящего
через небольшое отверстие в замкнутой полости. Однако, как следует из вышесказанного,
действительно равновесная плотность излучения в замкнутой полости может быть
достигнута только в том случае, если исключен полностью отток излучения из
полости.
При
равновесной плотности излучения атом испытывает равные давления двух идеальных
газов. При этом давление в атоме равно давлению в полости или давлению фононного
газа в твердом теле. Выравнивание внутреннего давления в самом атоме достигается
путем сдвига электронной оболочки, способность которой к деформации определяется
потенциалом ионизации.
Отсюда следует, что по внутреннему давлению сжатого атома можно определить равновесное давление излучения в полости.
Равновесное состояние двух систем можно описать
равенством
. (7)
Где 
, 
, - давление соответственно в атоме и полости; 
- обьем атома, 
-единица объема
полости.
Из формул (4) следует, что плотность излучения в световом потоке определяется одной частицей, которая находится в единичном объеме.
Для определения единичного
объема полости 
воспользуемся боровской
теорией водородного атома. Из этой теории следует, что если потенциальную
энергию сжатого граничного атома
преобразовать в кинетическую энергии электрона, то электрон
перейдет на одну из разрешенных орбит, где его энергия будет равна (3).
(8)
При этом радиус орбиты n определяется по формуле
(9)
где
- порядковый номер
орбиты
Далее
вычислим энергию в объеме сферы, радиус которой равен радиусу орбиты 
для n=1
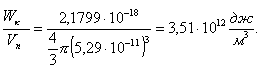(10)
Приравнивая 
к единичному объему 
, получаем равновесную плотность энергии излучения в
замкнутой полости.
Зная обьем фотона, вычислим
количество фотонов в объеме 1
:
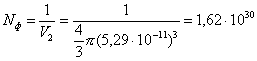фотонов.
Отсюда энергия излучения в 1
.
Далее вычислим при этой же
энергии количество фотонов в 1
по формуле (2):
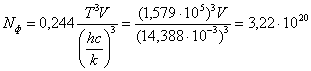фотонов.
При этом энергия излучения в 1
.
Полученное значение в 
раз меньше, чем энергия, вычисленная по формуле (10). В
приведенной формуле отсутствует обьем атома, что исключает возможность определения
равновесного состояния излучения с излучателем. Поэтому задача вычисления количество
фотонов в полости по одной температуре становится неопределенной.
Формуле (8) можно записать как
(11)
Из последнего равенства находим длину
волны 
(12)
Поскольку известны значения 
и 
, вычислим отношение
(13)
Обозначив полученное отношение как атомную константу
отметим, что
это отношение не зависит от порядкового номера орбиты электрона.
Далее
выразим кинетическую энергию электрона через температуру.
Для
n=1 
=1,579
K. Поскольку значения
и 
для уровня n=1
известны, то можно вычислить произведение
(14)
Для
сравнения вычислим 
при n=10. Для
этого уровня 
м., а 
. Отсюда
Далее
будем обозначать эту константу обозначать, как 
. Константа 
не зависит от уровня электрона и отражает закон сохранения
энергии.
Величину 
можно определить из равенства 
. Однако, важно показать, что 
можно определить,
используя атомную теорию Бора. Здесь 
имеет строго
определенный физический смысл, который заключается в том, что 
не зависит от уровня орбиты электрона. Постоянная 
указывает на то, что закон смещения Вина не согласуется с законами
сохранения и превращения энергии. Однако следует отметить, что 
не входит в формулы,
описывающие тепловое излучение без множителя 4,965. Умножая постоянную Вина 
на множитель 4,965, получаем 
, т.е тот же закон сохранения энергии.
Таким образом, получены две
константы 
и 
, в которых отражены физические свойства атома и закон сохранения
тепловой и электромагнитной энергии при их взаимном превращении.
При
вычислении формулы (10) значение радиуса орбиты 
для n=1
использовались справочные данные. Однако 
можно выразить через константы 
и 
.
В этом случае выражение для 
будет иметь вид
(15)
Подставляя
из формулы (15) в формулу (10), находим
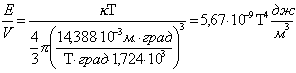. (16)
Формула
(16), как и формула (7) определяет равновесную плотность теплового излучения в
замкнутой полости. Она отражает свойства атома, закон сохранения энергии и согласуется
с атомной теорией Бора. Из формул (16) и (4) следует, что плотность в замкнутой
полости превышает плотность в потоке в 
раз.
Подставляя
в формулу (16) значение Т=1,579
получим
. (17)
Данный результат совпадает с величиной 
вычисленной по
формуле (10).
Затем,
подставляя в формулу (15) значение Т=1,579
имеем
(18)
Полученное
значение радиуса соответствует радиусу первой орбиты атома водорода.
При
экспериментальном подтверждении формул (1) и (16) достаточно в первом случае
измерить интенсивность излучения на выходе отверстия полости, во втором – измерить
давление в замкнутой полости без отверстия. В обоих случаях эксперименты проделаны
многократно и для различных целей. Давление в замкнутой полости измеряется при
установлении шкалы газового термометра или абсолютной термодинамической шкалы
Кельвина.
Колба
газового термометра помещается в термостат, которому задается требуемый уровень
температуры, при этом это количество газа в колбе можно изменять, приближаясь к
нулевому давлению.
Экспериментально
газовая шкала определяется соотношением (4):
, 
(19)
Здесь Т – температура,
подлежащая определению; 
- температура тройной точки воды.
Согласно (19) температура кипения
воды
(20)
Предел соотношения
устанавливается, экспериментально приближая давление газа в
колбе к нулю. Для воды 
, где 
- давление в колбе при температуре кипения воды и при 
.
Почему предел 
для воды стремиться к такому значению?
Этот вопрос при экспериментальном построении шкалы газового термометра не обсуждается.
Кроме того, для идеального газа, при сверхнизких давлениях и постоянном объеме равенство
(21)
(здесь К – постоянная Больцмана) должно выполнятся
при любом N. Однако при экспериментальном определении шкалы по
мере увеличения частиц газа в колбе термометра значение P/
изменяется.
Физическое обоснование работы газового термометра целесообразно рассматривать совместно с построением термодинамической шкалы Кельвина. Здесь же отметим, что равенство (21) является еще и отношением энергии. Действительно если в (21) числитель и знаменатель правой и левой части умножить на 3, то получим отношение энергии идеального газа.
Для отношения энергии
теплового излучения можно записать как
или 
(22)
Далее значение 
и 
вычисляем по формуле 
При 
, 
; при 
, 
.
Разделив 
на 
,получаем 
. Отсюда 
.
Таким образом, выражение (22) позволяет определить температуру излучаемого тела по длине волны спектра. Приведем примеры вычисления по формуле (22).
Выше отмечалось, что для
электрона уровня n=1 
. Находим соотношение
Используя формулу (22)
находим 
, что совпадает с температурой электрона уровня n=1, полученной
по данным теории Бора.
Известно, что длина волны в
максимуме спектра излучения Солнца за пределами атмосферы равно 
. Это позволяет записать отношение 
Отсюда определяем температуру
Солнца 
.
Согласно закону смещения
Вина температура Солнца 
. Однако, возбужденный атом до температуры 6000К не может
испустить квант электромагнитной энергии с длиной волны 
, поскольку это противоречит закону сохранения и превращения
энергии.
Реперные точки Международной практической температурной шкалы получены с помощью газового термометра. Их численное значение совпадает с численным значением, полученным при использовании соотношения (22). Это указывает на то, что определение температуры источника по формуле Вина приводит к ошибочным результатам. Эти ошибки имеют неустранимый характер.
Однако следует обратить внимание на то, что излучение может быть вызвано не только тепловым столкновением атомов, но, например, столкновением электронов с атомами при прохождении тока по проводнику. Или другой пример. Спектр тормозного рентгеновского излучения кроме коротковолновой границы практически не отличается от спектра теплового излучения. Если определить температуру катода по длине волны в максимуме спектра, то ее значение может достигать миллионы градусов Кельвина, но при этом катод, как источник излучения, будет находиться в твердом состоянии, т.е. ниже температуры плавления. Эти примеры указывают на то, что измерение температуры по длине волны излучения требует особой оговорки.
По-видимому, физически наиболее обоснованным источником теплового излучения может быть только одноатомный неполярный газ. Поскольку известно, что энергия излучения стенкой и его спектральный зависит от химической, термической и механической обработки поверхности этой стены. Механизм влияния обработки на излучение поверхности не установлен. Без учета этого влияния невозможно также определить температуру тела. Однако по излучению стенкой можно судить о том, что плотность этого излучения ниже плотности излучения полостью через небольшое отверстие. Отсюда следует, что максимальная плотность энергии теплового излучения достигается в замкнутой полости, т.е. в полости без отверстия. Промежуточную плотность излучения можно получить при выходе излучения через небольшое отверстие в полости. Наименьшая плотность получается при излучении стенкой в пустое пространство.
При температуре Т=
давление создаваемое излучением в полости без отверстия
будет 
. Такое давление может оказывать существенное влияние на
состояние реального газа. Однако взаимодействие излучения с реальным газом
следует описать отдельно.
Литература
1.
Майер
Дж. и Гипперт-Майер М. Статистическая механика. М.: Мир, 1980, 554с.
2.
Ландау
Л.Д. и Лившиц Е.М. Статистическая физика. Часть 1.М.: Наука, 1976, 583с.
3.
Савельев
И.В. Курс общей физики, том III. М.: Наука, 1973, 305с.
4.
Фен
Дж. Машины, энергия, энтропия.М.: Мир, 1986, 333с.
CONCERNING AN ERROR IN THEORY OF THERMAL RADIATION
Konov A. F.
Examples of the contradictions in theory of thermal radiation are given
in this paper. Elimination of the contradictions allows to determine that the
equilibrium density of radiant energy in a closed cavity exceeds the density of
energy in the flux of radiation by 7,5
times. The formula for calculation of energy
in the closed cavity is obtained on the base of the Bohr's theory of the hydrogen
atom.
The relation that binds the law of thermal radiation with the Kelvin’s
absolute thermodynamic scale is obtained as well and presented in this paper.
Key words: thermal radiation, wave length, radiation
spectrum peak, Planck’s formula, Wien displacement law, radiation pressure in
the closed cavity.
ГУ Всероссийский научно-исследовательский
институт сельскохозяйственной метеорологии
(ГУ ВНИИСХМ) г. Обнинск
Поступила в редакцию 10.11.2011