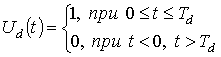Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 10. -

Вып. 4. - 2011. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-32-html/TITL-32.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-32-html/cont.htm

 

 

УДК 621.390

 

АНАЛИТИЧЕСКОЕ ОПИСАНИЕ ЧАСТОТНО-ВРЕМЕННОГО ПАРАМЕТРА РАССЕИВАНИЯ РАДИОИМПУЛЬСА С ВУХЧАСТОТНЫМ КФМ СИГНАЛОМ

 

Ó 2011. г. Коцур А. А., Усов М. П.

 

(kotsur.doc)

 

Рассматривается аналитическое описание частотно временного параметра для двухчастотного радиоимпульса с прямоугольным законом амплитудной модуляции.

Ключевые слова: КФМ сигнал, аналитическое описание.

 

Решение задачи по нахождению аналитического описания частотно-временной параметра рассеяния и приема будем искать во временной области, сформированной двухчастотным КФМ сигналом и  описываемой выражением

 

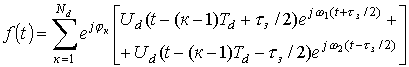                          (1)

 

где  Nd

-

число дискретов в КФМ радиоимпульсе;

-

начальная фаза к-го дискрета;

-

закон модуляции дискрета;

;

Td

-

длительность дискрета;

tз

-

время между излучениями сигналов на разной частоте;

w1,

w2

-

несущая частота КФМ радиоимпульсов;

Импульсная характеристика согласованного фильтра есть функция комплексно сопряженная функции зондирующего сигнала

 

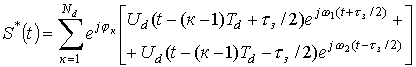            (2)

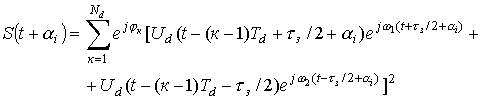    (3)

сигнал на входе СФ, отраженный от i-ой БТ без учета .

Определим  значение нормирующего коэффициента Q .

Для упрощения выкладок введем обозначения:

 

;

.

Раскроем квадрат модуля как произведение комплексно сопряженных функций  и .

 

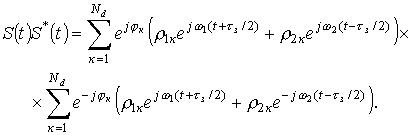
Результатом произведения сумм будет матрица из Nd Nd  элементов. Элементами матрицы будут составляющие вида Вк В*к (диагональ матрицы), Вк В*z и Вz В*к , где к=1.. Nd , z=(к+1).. Nd . Определим значения элементов матрицы.

 

;

.

 

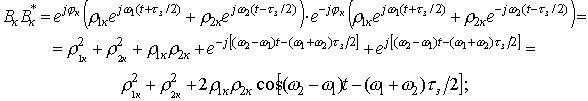
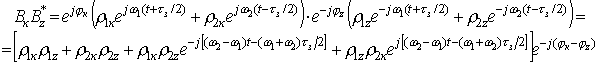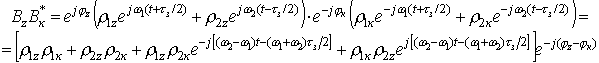Представим сумму элементов Вк В*к матрицы в виде

 

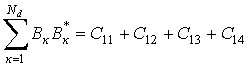,                           (4)

где

;    ;

;   ;

;   .

 

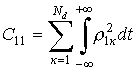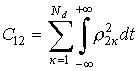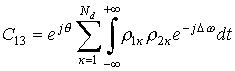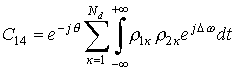Проведем расчет каждого слагаемого суммы (4)

;

.

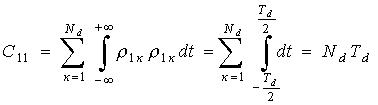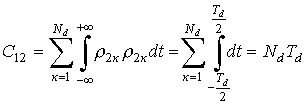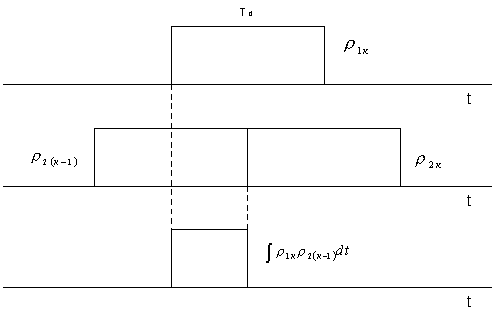
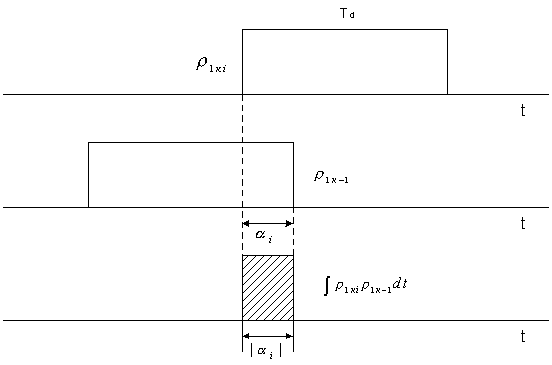
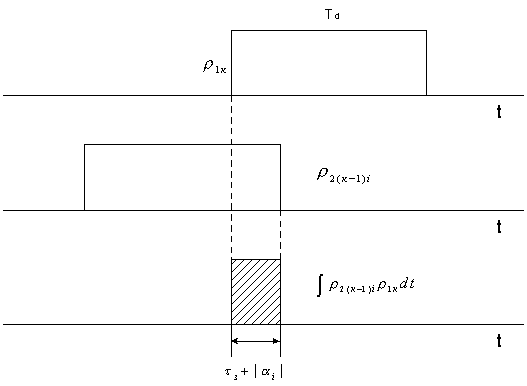
Изменяя пределы интегрирования, выбор которых поясняет рис. 1 получим

 

;

;

;

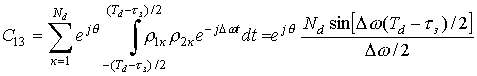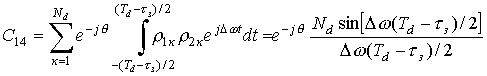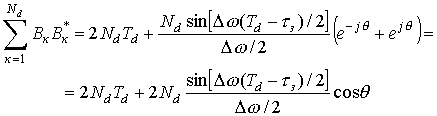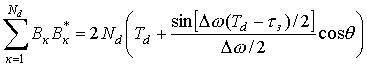.                               (5)

 

 

Аналогичным образом представим сумму элементов Вк В*z  матрицы в виде

 

,

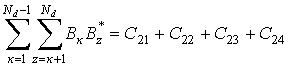  (6)

где  ; ;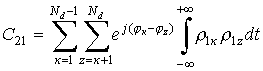

; .

 

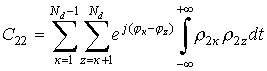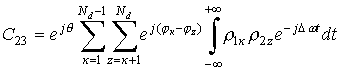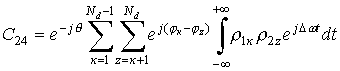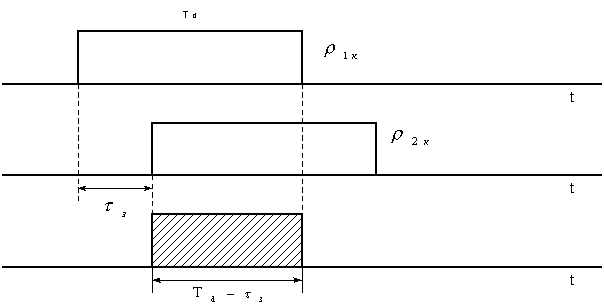
Рисунок 1

 

Из всей выборки сумм С21 и С22 значения интегралов равны нулю, что для примера поясняется рис. 2 для интегралов суммы С21 . Таким образом С21=С22=0.

Из всей выборки сумм С23 ненулевое значение интеграла имеется только для сочетания . Изменяя пределы интегрирования, выбор которых поясняет рис. 3 имеем

 

.

 

 

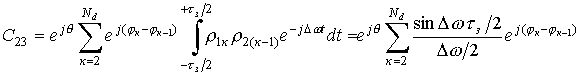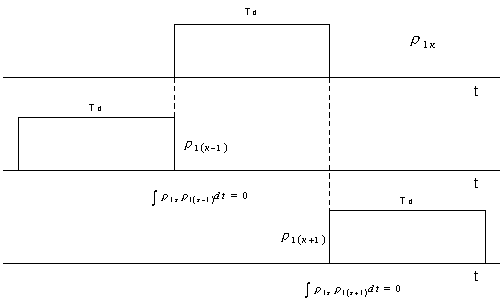
Рисунок 2

 

Аналогичным образом получаем решения для С24

 

.

 

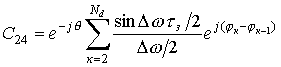Используя результаты составляющих суммы, имеем

 

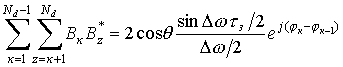.              (7)

 

 

Рисунок 3

Используя алгоритмы вычисления суммы элементов Вк В*z решение для суммы элементов Вz В*к может быть определено в следующей форме записи:

 

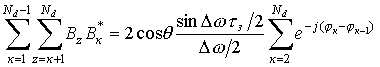.                   (8)

Суммируя результаты (5), (7), (8) получаем значение интеграла для  двухчастотного КФМ сигнала

 

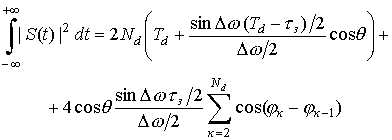                            (9)

 

Находим значение нормирующего множителя  Q

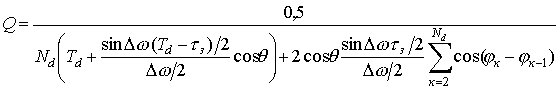                                                                            (10)

 

Для нахождения аналитического описания частотно временного параметра рассеяния и приема двухчастотного КФМ сигнала воспользуемся выражением

 

.

 

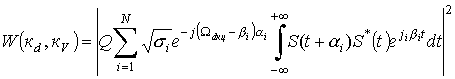Произведем преобразования с использованием выражений (2), (3). Для упрощения записи введем обозначения:

 

;

.

 

Вычислим произведение подынтегрального выражения

 

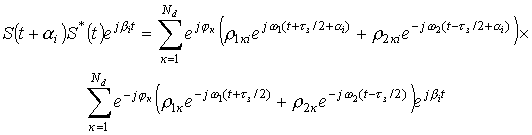
Результатом произведения сумм будет матрица с элементами Тк Т*к , Тz Т*к , Тк Т*z , где к=1..Nd . Определим значения элементов матрицы

;

;

.

 

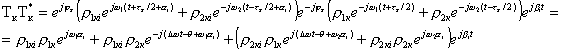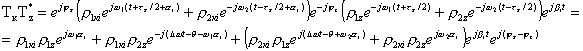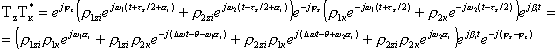Представим сумму элементов Тк Т*к  матрицы в виде

 

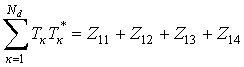,                              (11)

где    ;  ;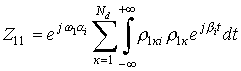

;

.

 

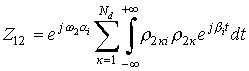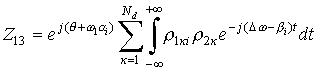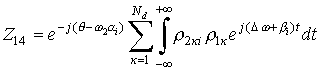Проведем расчет каждого слагаемого суммы выражения (11). Изменяя пределы интегрирования, выбор которых поясняет рис. 4 для элементов Z11, Z12 получим

 

;

.

 

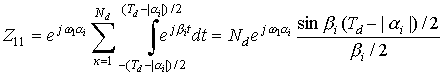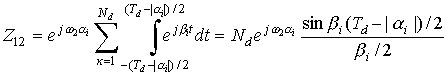Изменяя пределы интегрирования для слагаемых Z13, Z14 получаем:

 

;

.

 

 

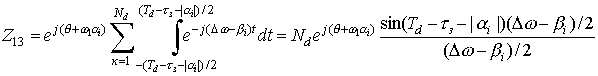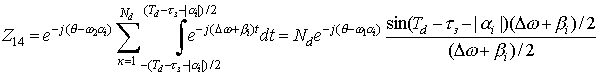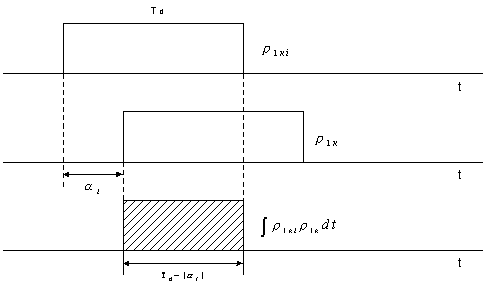
Рисунок 4.

 

Подставляем полученные результаты в выражение (1)

 

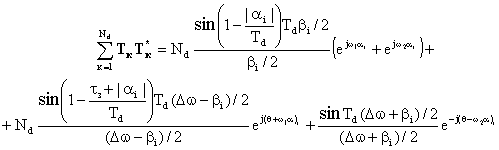                 (12)

 

 

Рисунок 5

 

Аналогичным образом представим сумму элементов Тк Т*z  матрицы в виде

 

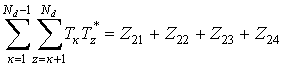,                          (13)

где                         ;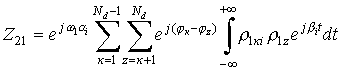

;

;

.

 

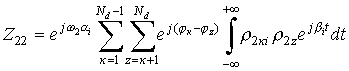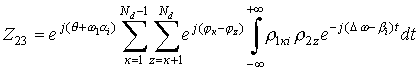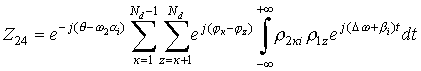Проведем расчет каждого слагаемого суммы выражения (13). Из всей выборки сумм слагаемых Z21 и Z22 ненулевое значение интеграла имеется только для сочетаний  и . Для наглядности решения интеграла слагаемого Z21 поясняется рис. 6.

 

 

Рисунок 6

;

.

 

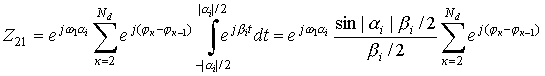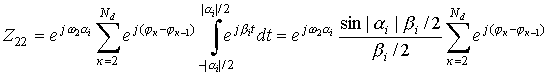Изменяя пределы интегрирования для слагаемых Z23, Z24 ( рис.7) получаем:

 

;

.

 

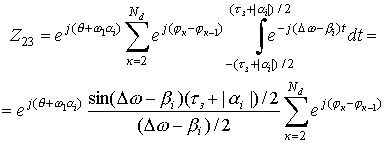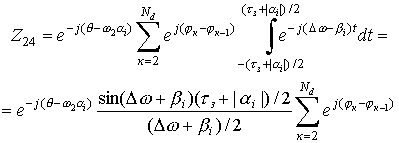Подставляем полученные результаты в выражение (13)

 

 

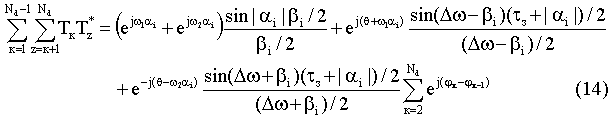
Используя алгоритмы вычисления суммы элементов Тк Т*z решение для суммы элементов Тz Т*к  может быть определено в следующей форме записи:

 

 

 

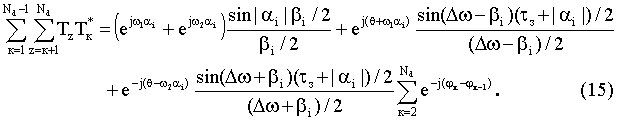
Рисунок 7

 

Суммируя результаты выражений (12), (14), (15) получаем значение интеграла выражения с учетом множителя

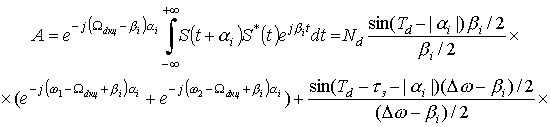
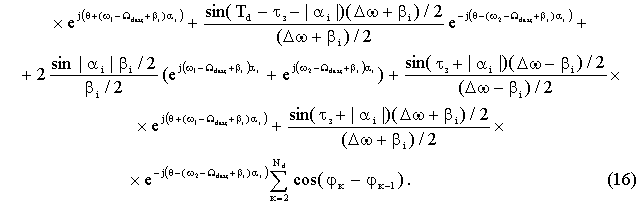
Введем вспомогательные переменные

 

 ,  ,

,           ,

 ,    ,

 ,    ,  .

 

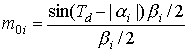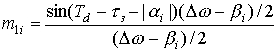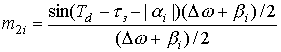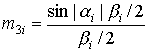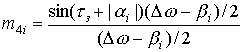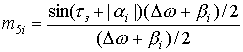Подставим их в выражение (16) и приведем подобные.

 

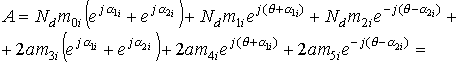       (17)

.

 

Введем вспомогательные переменные

 

; ; .

 

С учетом последнего выражение (17) примет вид

 

.                (18)

 

Используя выражения (18) получаем

.

 

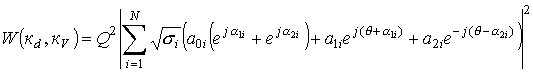Раскроем квадрат модуля |D|2=DD* . Произведение сумм D и D* запишем в виде матрицы

 

.

 

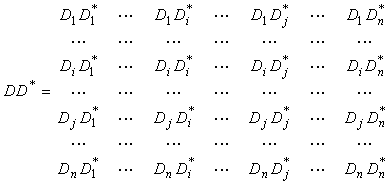Вычислим значения элементов главной диагонали матрицы

;

;

;

;

;

;

;

;

.

 

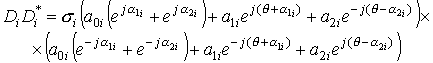
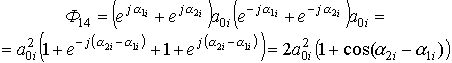
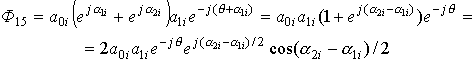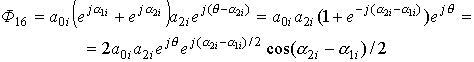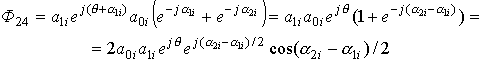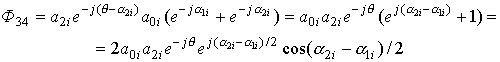После приведения подобных имеем

 

      

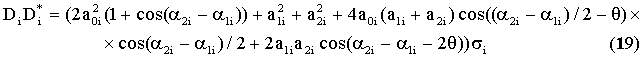
 Определим значения элементов DiD*j

 

. ;

;

;

;

;

;

;

;

;

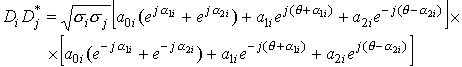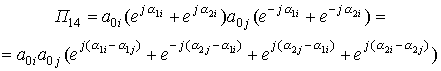.    (20)

 

Найдем значения элементов матрицы DjD*i

 

              (21)

.

 

Объединяя равенства (20) и (21) имеем:

 

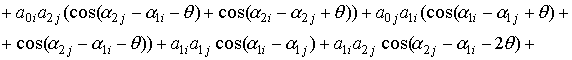
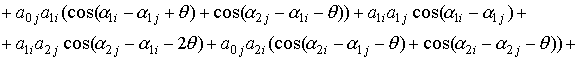
 .                           (22)

 

Суммируя значения элементов матрицы (19) и (22) получаем аналитическое описание частотно временного параметра для двухчастотного КФМ сигнала с учетом времени запаздывания их излучения (tз < Td )

 

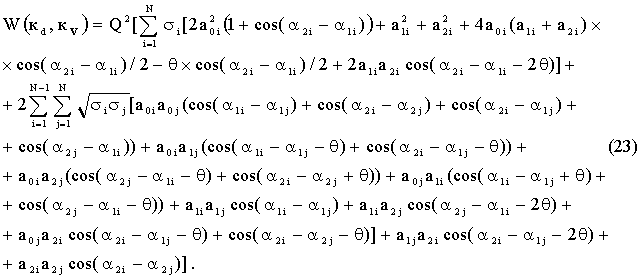
При tз =0 (q=0) выражение (23) примет вид

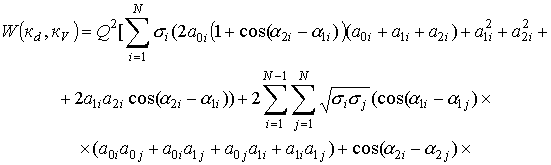
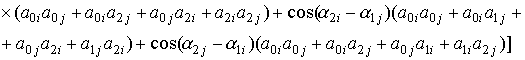 (24)

 

Несмотря на громоздкость, выражение (24) позволяет перейти к аналитическому описанию частотно временного параметра других, в том числе более простых радиолокационных сигналов.

Для КФМ сигнала с одной несущей частотой w1=w2=w0  выражение (24) примет вид

 

 

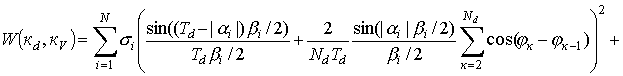
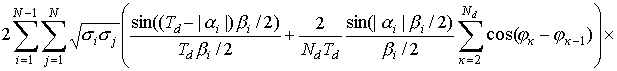
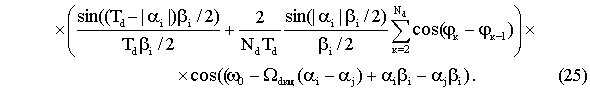
Аналитическое описание частотно временного параметра для двухчастотного радиоимпульса с прямоугольным законом амплитудной модуляции получается из выражения (24), если принять Nd =1, Тd =tз . При этом выражение имеет вид:

 

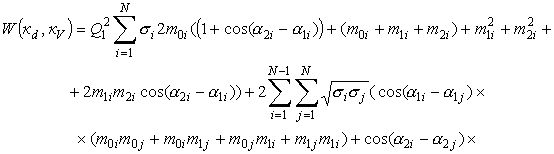
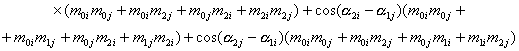, (26)

 

где

.

 

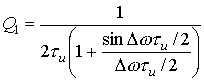Составляющие вида moi , m1i , m2i описываются выражениями (а) при условии tз =0.

Выражение для двухчастотного сигнала получается из выражения (26) при условии tи→¥, что длительность импульса приближается к бесконечности, тогда

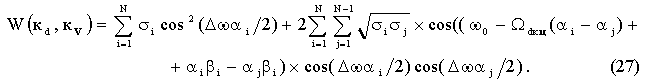
Если в выражении (26) принять Dw=0, то можно придти к выражению (4), описывающему частотно временной параметр рассеяния и приема РИ с прямоугольным законом амплитудной модуляции.

Полученные аналитические выражения могут быть использованы при разработке систем распознавания в которых используются КФМ сигналы.

 

 

THE ANALYTICAL DESCRIPTION OF TIME-AND-FREQUENCY PARAMETER OF DISPERSION OF THE RADIO IMPULSE WITH THE TWO-FREQUENCY KFM SIGNAL

 

Kotsur A. A., Usov M. P.

 

The analytical description is considered is frequency time parameter for a two-frequency radio impulse with the rectangular law of peak modulation.

Key words: KFM signal, analytical description

 

Военная академия войсковой ПВО Вооруженных Сил Российской Федерации

имени Маршала Советского Союза А.М. Василевского                                                                        

(ВА ВПВО ВС РФ)

Поступила в редакцию 30.09.2011.