Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 10. -
Вып. 4. - 2011. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-32-html/TITL-32.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-32-html/cont.htm
УДК [611.13/.16+611.423]:616-006-092.9
Распространение пульсовой волны по
большим кровеносным сосудам
Ó 2011 г. Меркулов В. И.
В работе с помощью математического моделирования изучаются
процессы распространения пульсовой волны по крупным кровеносным сосудам. В
частности объясняется наблюдаемый эффект повышения амплитуды по мере удаления
от сердца источника пульсовой волны. Отдельно рассматривается вопрос об определении
полного артериального давления, для чего используется зависимость скорости
распространения пульсовой волны от
среднего давления.
Ключевые слова: математическое
моделирование, пульсовая волна, кровеносные сосуды, полное артериальное давление.
Введение
Система кровообращения для каждого живого организма
является важнейшей системой, нормальное или патологическое функционирование которой
определяет нормальное или патологическое
функционирование всего организма.
Механике кровообращения посвящено огромное количество научных работ и монографий. Из отечественных монографий укажем на коллективную монографию [1] и обзор [2], из зарубежных монографию [3], в которой можно найти достаточно полное изложение проблемы и обширную библиографию. В этих книгах нас будут интересовать особенно те аспекты проблемы, которые, по мнению авторов, не получили достаточного объяснения.
В монографиях [3, 4] излагается теория пульсового движения крови в сосудах, и приводятся экспериментальные данные по распространению пульсовой волны вдоль сосудистого русла. Обращает на себя внимание тот факт, что по мере продвижения волны по всем крупным артериям и аортам ¾ восходящая аорта, грудная аорта, брюшная аорта, бедренная артерия, большая подкожная артерия ¾ амплитуда пульсовой волны возрастает почти в два раза, а среднее давление сохраняется на входном уровне, как это показано на рис.1, заимствованном из монографии [3].
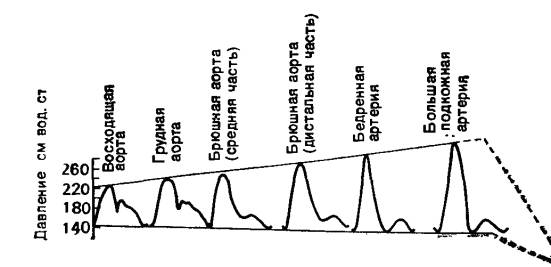
Рис. 1
Это тем более удивительно, что волна на своем пути несколько раз проходит точку
бифуркации, последовательно переходит в сосуды меньшего диаметра.
Стенки крупных кровеносных
сосудов кроме эластичных материалов включают в себя мышечные волокна. Их
функция в работе сердечно-сосудистой системы
особенно важна, если учесть, что потребление кислорода этими мышцами,
которое определяет их энергетику, на порядок превышает потребление кислорода
скелетной мускулатурой в покое [5].
Обычно роль сосудистых
гладких мышц сводят к управляемому изменению упругости стенок сосудов, что
называют тонусом. Легко понять, что упругость стенок сосудов, независимо от
того, является она управляемой или неуправляемой, не меняет энергетику процесса
кровотока и не способна поднять амплитуду импульсной волны.
В попытках объяснить эффект
увеличения амплитуды пульсовой волны мы обратили внимание на открытый сто лет
назад эффект, который получил название феномен Остроумова-Бейсселя [6].
Этот эффект состоит в том,
что на быстрое растяжение гладкие мышцы реагируют повышением напряжения. Этот
механизм наблюдается даже в отсутствие нервных волокон и, следовательно, не
требует участия нервной системы.
1. Физическая постановка задачи
Рассмотрим движение несжимаемой жидкости, в данном случае крови, по трубке, стенки которой способны растягиваться под действием внутреннего давления и сжиматься не только под действием упругих сил, но и под действием гладких мышц, включенных в стенки кровеносного сосуда.
В отличие от упругой силы,
которая по величине и фазе определяется величиной и фазой деформации, величина
и фаза сокращения мышечных волокон может иметь другие значения, что и
определяет ее активную функцию. При этом движение крови будет вызываться не
только действием перепада давления, в рассматриваемом случае ¾ импульсного перепада давления,
но и под действием ответной деформации стенок сосуда. Кровь будет рассматриваться
как ньютоновская вязкая несжимаемая
жидкость, текущая в ламинарном режиме.
2. Математическая модель процесса
В кровеносном сосуде выделим
элементарную струйку тока по направлению движения крови. Введем обозначения: w ¾ вектор скорости, ориентированный
вдоль струйки, df ¾ площадь поперечного сечения
элементарной струи, r ¾ плотность крови.
Количество жидкости, которое
протекает через рассматриваемое сечение, будет равняться 
Уравнение импульса вдоль
струи запишется в виде
(1)
Здесь p ¾ давление в текущей точке
струи, 
¾ постоянный для ламинарного течения коэффициент, определяющий
гидравлическое сопротивление для жидкости с кинематической вязкостью n, текущей в канале диаметром d.
В уравнении (1) опущено
слагаемое 
, что соответствует малости динамического давления по
сравнению со статическим давлением 
, которое считается независящим от поперечной координаты.
Для этой же струйки должно
выполняться уравнение неразрывности
(2)
Суммируя по всему сечению
соотношения (1) и (2), получим следующие дифференциальные уравнения:
(3)
(4)
где 
¾ массовый расход.
Приведенная
система уравнений использовалась в монографии Чарного [7].
Для замыкания системы
уравнений (3),(4) необходимо указать связь между изменением площади поперечного
сечения и давлением. В пассивном
упругом сосуде эта связь определяется законом Гука, который для малой деформации
записывается как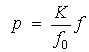
, где 
¾ среднее значение площади
поперечного сечения, K ¾ его жесткость на
растяжение.
Для активно-упругого сосуда
нужно указать связь между скоростями изменения давления и площади поперечного
сечения в соответствии с феноменом Остроумова-Бейсселя и законом Гука[9]:
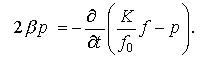(5)
Коэффициент 2
определяет ту долю давления, которая вызывается работой
сосудистой мускулатуры и подлежит определению по экспериментальным данным.
С использованием соотношения
(5) линеаризованные уравнения (3), (4) запишутся в виде
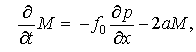(6)
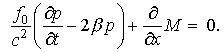(7)
Здесь использовано
обозначение 
Перекрестным
дифференцированием исключим из системы уравнений (6), (7) давление и получим
одно уравнение для массового расхода.
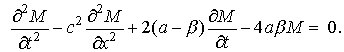(8)
Исключая массовый расход,
получим такое же уравнение для давления
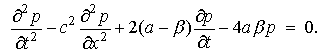
Уравнение
(8) является хорошо изученным телеграфным уравнением.
Введя в рассмотрение
безразмерные независимые переменные 
, мы сможем получить уравнение в безразмерной форме:
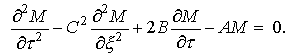(9)
И
такое же уравнение для давления.
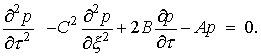(10)
Здесь 
¾ безразмерная скорость
распространения пульсовой волны, 
¾ логарифмический декремент
затухания (нарастания) волны, 
3. Периодическое течение в артериальном русле
Идентификация выбранной математической модели требует
выбора входящих сюда параметров по условию согласования результатов вычисления
и наблюдения. Если работу сосудистой мускулатуры приравнять работе сил вязкости,
то это позволит определить параметр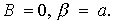 
При этом уравнение
для волны давления приобретет вид
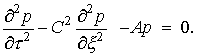
Периодическое решение этого
уравнения можно искать в виде
,
Уравнение для амплитудной
функции запишется как 
где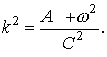 
В свою очередь решение этого
уравнения имеет следующий вид:
.
Входящие сюда постоянные
коэффициенты могут быть выражены через амплитудные
значения давления и градиента давления на входном конце сосуда:
.
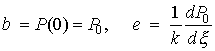Нерегистрируемый
в эксперименте входной градиент давления с помощью уравнения импульса выразим
через регистрируемую величину массового расход.
Уравнение импульса в
пренебрежении вязких сил в безразмерной форме запишется так:
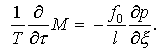
Учитывая временные
зависимости
,
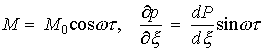получим
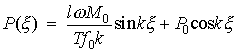. (11)
Исходные данные для
числового примера мы возьмем из монографии [3] применительно к кровеносной
системе собаки.
В
теории импульсного движения крови используется безразмерный параметр Уомерсли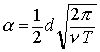 
[3]. Здесь d —
диаметр кровеносного сосуда, T ¾ период пульсационного течения, 
кинематическая вязкость крови.
Коэффициент гидравлического
сопротивления, который входит в наши уравнения, может быть выражен через
параметр Уомерсли следующим образом
Параметр Уомерсли для
различных участков артериального русла имеет значения в интервале 3,5—12. Для
определения закона распространения волны давления нет необходимости знать
численное значение параметра Уомерсли, достаточно знать, что для крупных
кровеносных сосудов он имеет значение значительно больше единицы. Из этого
будет следовать малость гидравлического сопротивления по сравнению силами
инерции. То же самое относится к скорости распространения пульсовой волны.
Литературные источники указывают различные значения от 8 до 10 м/с в
зависимости от тонуса сосудистой системы.
Для других параметров
выберем следующие значения: T =
0,4 с, С = 10 м/с, 
.
По этим данным, применяя формулу (11), находим
. По литературным данным (3) артериальное давление в
подкожной артерии собаки в полтора раза больше давления сердечного выброса. Как
видим, принятая математическая модель в предположении 
позволяет получить
удовлетворительное согласие с наблюдением.
Строго говоря,
кровеносную систему нужно рассматривать как некоторую сеть. Принятая выше
математическая модель применима только в пределах от одной точки ветвления до
другой. Определение краевых условий в этих точках требует составления системы
уравнений, охватывающей всю сеть кровеносных сосудов. Для построения линейной модели, применимой к большому участку кровеносного русла, мы должны выделить
тонкую струйку, которая без ветвления проходит от сердца до запястья.
Применение уравнений (9) и (10) к такой
струйке возможно только при выполнении специальных условий. На всем своем
протяжении струйка переходит из одной артерии в другую, которые отличаются своим
диаметром, а ,следовательно,
гидравлическим сопротивлением, могут отличаться скоростью распространения
пульсовой волны С и скоростью течения крови. Принятое нами условие В=0, которое
соответствует равенству работы мускулатуры работе сил вязкости, обеспечивает нулевое гидравлическое
сопротивление вдоль всего русла. Мы
вправе ожидать, что упругие и геометрические параметры артерий в точках
ветвления меняются так, что скорость распространения пульсовой волны С и
скорость кровотока 
сохраняют свое значение. В противном
случае в каждой точке ветвления
пульсовая волна будет отражаться, а
импульс теряться.
Из приведенного ниже рисунка следует, что скорость течения в сосудах сохраняется постоянной в плоть до миллиметровых размеров.
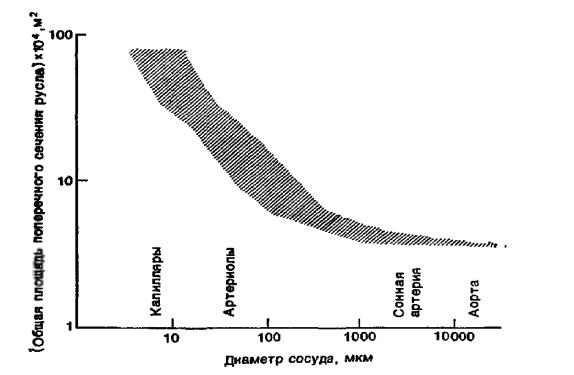
Рис.2.
Физическое условие поглощения
пульсовой волны в мелких артериях кисти, по-видимому, хорошо согласуется использованным
нами условием периодического решения в полубесконечном русле.
Выполнение перечисленных
условий обеспечивает применимость принятой
нами линейной модели и объясняет хорошее согласование расчетных и наблюдаемых величин.
Полезно сравнить полученное
решение с законом распространения периодической волны по пассивному упругому
каналу. Такое движение описывается тем же уравнением (10)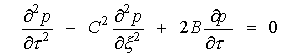 
при значении параметров
. Как известно [8], решение такого уравнения имеет следующий
вид: 
, где функция 
является решением волнового уравнения без
диссипативного члена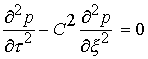 
, которое описывает незатухающие колебания.
Отсюда можно видеть, что в
то время как активно-упругий кровеносный сосуд обеспечивает незатухающие
колебания, течение в пассивном упругом
сосуде сопровождается затуханием амплитуды по экспоненциальному закону.
Чтобы определить
количественно величину затухания, рассмотрим некоторый пример. Для этого
выберем среднее значение параметра Уомерсли равное 8. По нему определим
величину 
и величину уменьшения
амплитуды волны за период 
.
Определение
давления по скорости течения
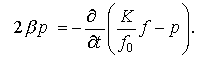
Ультразвуковыми методами можно
измерить среднюю по сечению скорость
движения крови 
и скорость изменения
площади поперечного сечения f(x,t)
В то время как для целей
диагностики требуется знание давления p(x,t) и массового расхода M(x,t),
который так связан со скоростью и площадью поперечного сечения
Последнюю формулу можно заменить приближенной зависимостью
,
которая
позволяет определить массовый расход по результатам измерения скорости и
площади поперечного сечения.
Для стационарных течений закон Гука позволяет выразить давление через деформацию сосуда
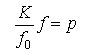
В предыдущих вычислениях мы использовали такую зависимость давления и площади поперечного сечения
(14)
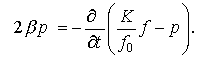
которая учитывает как закон Гука, так и закон
Остроумова-Бейсселя.
Представим измеряемую
функцию 
в виде суммы
и перепишем уравнение (14) следующим образом
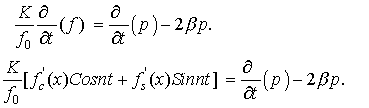
Подвергнем последнее уравнение преобразованию Фурье.
В результате можно получить систему уравнений
(15) 
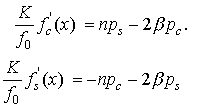
Где
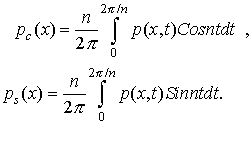
коэффициенты Фурье.
Разрешим систему
уравнений (15)
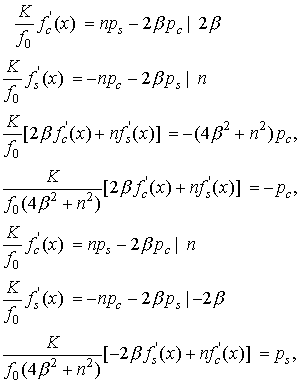
Окончательно получим
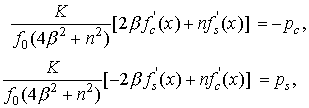
Знание коэффициентов Фурье позволяет определить
давление по известной формуле
4. Среднее артериальное давление
Рассмотренная выше пульсовая
волна представляет собой колебания возле некоторого среднего значения. Однако
диагностическим показателем является величина полного давления, систола и
диастола. В стационарных условиях эта величина определяется с помощью манжеты,
которая обеспечивает переменное давление на кровеносный сосуд. Для целей круглосуточного мониторинга такой
способ оказывается очень не удобным.
Для определения среднего
давления можно использовать зависимость скорости распространения пульсовой
волны от величины среднего давления.
На приведенном ниже рисунке, который мы позаимствовали из цитированной
ранее монографии [3] приведена такая зависимость для собаки.
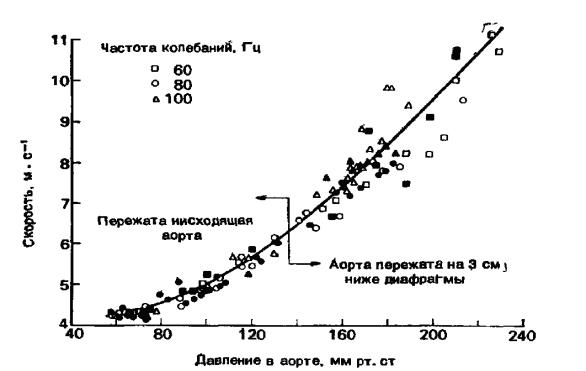
Обработка этой
экспериментальной зависимости позволяет получить аналитическую зависимость
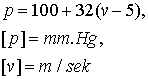
с помощью
которой можно определить величину среднего значения давления по результатам
измерения скорости распространения пульсовой волны.
Такую же зависимость можно получить и для человека с некоторыми другими числовыми параметрами.
По этой формуле можно определить чувствительность принятого способа.
Изменение давления на 10мм. рт. ст. приведет к увеличению скорости распространения пульсовой волны на 0.31м/сек.
Отдельному рассмотрению подлежат вопросы разброса экспериментальных точек, требуемая точность измерения и вариабельность параметров в зависимости от состояния человека.
Заключение
Полученные
результаты позволяют лучше понять активную роль сосудов в работе всей сердечно
сосудистой системе.
Удается
лучше понять, как отличия в морфологии стенок артериальных и венозных сосудов
приводят к различной их функции в механики кровообращения. В свою очередь это
позволяет глубже решать вопросы, связанные с диагностикой
работы сердечно-сосудистой системы и протезированием ее элементов.
литература
1.
Физиология
кровообращения. Физиология сосудистой системы. Л.: Наука, 1984, 643 с.
2.
Павловский Ю. Н.,
Регирер С. А., Скобелева И. М. Гидродинамика крови // Итоги науки. М.: ВИНИТИ,
1970. Сер. Гидромеханика, 1968.
3.
Каро К., Педли Т.,
Шротер Р., Сид У. Механика кровообращения. М.: Мир, 1982. 624 с.
4. McDonald D.A. Blood
Flow in Arteries. Baltimore: Williams, Wilkins, 1974. 496 p.
5.
Lehninger A.L. The metabolism of the arterial wall. In The Arterial
Wall. Baltimore: Williams, Wilkins, 1959. P.
220–246.
6.
Орлов Р.С. Попов С.В. Влияние
растяжения на сократительные ответы гладкой мускулатуры изолированной воротной
вены // Физиолог. журн. СССР. 1977. Т. 63, №2. С. 303–312.
7.
Чарный И.А.
Неустановившееся движение реальной жидкости в трубах. М.: Недра, 1975. 296 с.
8.
Смирнов В.И. Курс высшей математики. Т. 2. М.; Л.: ГИТТЛ, 1952. 628 с.
9.
Меркулов В. И. Новые
открытия и новые задачи гидромеханики. Изд. НГТУ, Новосибирск, 2010, 160 с.
Работа поддержена грантом 13.G25.31.0071
(H-01/08-10)
Меркулов Владимир Иванович
Доктор физ-мат наук, Главный научный сотрудник,
профессор
Новосибирский государственный университет
Институт теоретической и прикладной механики СО РАН
Поступила в редакцию
4.10.2011