Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 10. -
Вып. 4. - 2011. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-32-html/TITL-32.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-32-html/cont.htm
Поиск условий культивирования, влияющих на синтез микроорганизмами
экономически значимого продукта
Ó2011 г. Шулюпин О. К.
Биологические системы, зависящие от большого
количества факторов с сильным межфакторным взаимодействием при современных требованиях
практики сложно изучать, моделировать и управлять процессом на основе мало
связанных однофакторных зависимостей по методу Зайделя-Гаусса. Методология
проведения однофакторных зависимостей хорошо разработана и в дополнительных
объяснениях, на наш взгляд, не нуждается
[1].
Представление полученных нередко весьма разнородных результатов измерений в виде графиков, таблиц, корреляционных полей, нахождение аналогий с более изученными родственными объектами служат основой к проведению активных поисковых работ и дальнейшей оптимизации процесса с количественным учетом влияния нескольких факторов на синтез целевого продукта.
Состояние популяции микробов
существенно зависит от разнообразных по своему характеру (качественно
различных) и по интенсивности (количественно различных) факторов. Поэтому пред
современным микробиологом стоит задача – комплексное исследование объекта,
установление причинно-следственных связей между различными явлениями, выделение
управляемых факторов и воздействие на них. Молекулярное клонирование не решает
проблемы, т.к. в состав гибридного репликона переносят структурный ген вместе с
регуляторными участками.
Микроорганизмы способны расти на
субстратах, недоступных другим живым системам [2], а так же имеют большое
прикладное значение в качестве вакцин в
медицине и ветеринарии и продуценты антибиотиков и других физиологически активных
веществ. Но геном каждого микроорганизма кодирует 2 - 3 тысячи белков [2, 3],
далеко не все из которых представляют интерес.
Кроме того, нередко гены, ответственные за такие белки, находятся под сложной
регуляцией компонентами питательной среды [1- 4].
Среди микробиологов известны
следующие задачи - есть некий штамм, который продуцирует нужный продукт при культивировании
на плотной среде, либо в организме животного, но не продуцирует при глубинном
культивировании. Такой организм не продуцирует
пи культивировании на простых питательных средах на основе гидролизатов
и вытяжек природного сырья, либо синтез представляющего интерес продукта при
глубинном культивировании зависит от
партии питательной среды. Как правило, это означает, что в питательной среде
должны присутствовать индукторы или метаболизируемые ингибиторы нужных
синтезов.
С точки зрения молекулярной
биологии, структурный ген может находиться под регуляцией любым промоторно –
операторным участком и регуляторным фактором может быть любая комбинация из
индивидуальных компонент питательной среды или интенсивностей физико-химических
факторов (температура, рН и т.д.). Причем за счет рекомбинационных процессов,
прочих внутригеномных перестроек и спонтанного мутагенеза конкретное сочетание
промоторно-операторный участок - структурный ген будут носить
штаммовоспецифичный характер [1-5].
По нашему мнению, часть задач такого
типа можно решить, если перейти к средам максимально известного, контролируемого
химического состава, в том числе и к синтетическим питательным средам.
Проведение поиска возможных
регуляторных факторов иногда бывает проще осуществить путем конструирования семейства
сред известного химического состава из индивидуальных химических соединений,
синтетических питательных сред и добавок
известных компонентов к питательным средам неизвестного состава,
уменьшив до минимума компоненты типа сыворотки, крови или иного продукта из
сырья природного происхождения с неизвестным составом. В идеале, вообще отказавшись
от таких добавок. Тем не менее, осталось ряд проблем, мешающих широкому
применению вышеназванных возможностей.
Несмотря на то, что в литературе
описано колоссальное количество сред известного химического состава и синтетических
питательных смесей и добавок для представителей различных таксономических групп
микроорганизмов и культур эукариотических клеток, в литературе описана лишь
очень общая стратегия конструирования таких сред. Недостаточно подробно рассмотрена
роль активного многофакторного
отсеивающего эксперимента для поиска регуляторных факторов нужных синтезов /2,4,5/, отсутствуют четко
сформулированные критерии оптимальности поиска, а также недостаточно подробно
прокомментированы слабые места и области применимости двухуровневых
оптимизационных экспериментов. Планы трех – и более уровней варьирования
управляемых переменных в литературе упоминают, но не приводят в конкретных
работах и руководствах. В предлагаемой работе сделана попытка восполнить
указанные пробелы в практической теории планирования эксперимента на примере
микробиологических задач.
Выход процесса (ВП), в зависимости от концентрации регуляторных
компонентов питательной среды (интенсивности фактора) имеет сложный вид. В
общем случае это многомерная поверхность (поверхность отклика), о форме которой
можно сделать достаточно общие предположения на основании большой работы,
проведенной при изучении значительного количества конкретных объектов и
опубликованных в многочисленных статьях и руководствах, а так же на основании
собственных неопубликованных ранее данных.
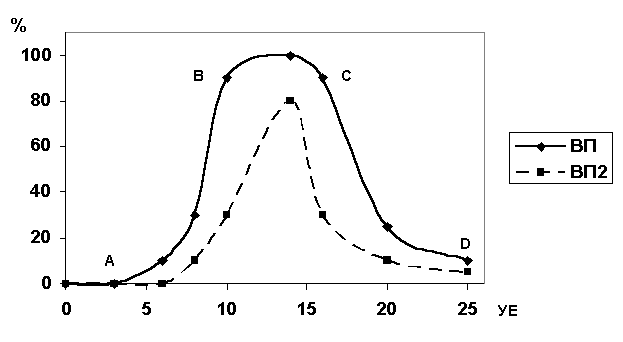
Рис. 1. Зависимость ВП от концентрации
метаболизируемого индуктора в питательной среде.
В простейшем случае, когда ВП
зависит от одного фактора, можно отобразить
зависимость в виде двумерной кривой, рис.1. Можно выделить следующие
участки 0 – А допороговый уровень концентрации регуляторного фактора,
нераспознаваемый микроорганизмом, не вызывающий нужного синтеза, А – В участок
лимитирования, В – С уровень насыщения
влияния регуляторного фактора, С –D
участок ингибирования нужного синтеза
контролируемым фактором (группой факторов). На рис.1 отображен наиболее
общий случай. Углы наклона кривой в каждой точке будут строго индивидуальны и
могут варьировать в широких пределах. В частности, некоторые факторы могут не
достигать уровня ингибирования, прерываясь на т.С. При влиянии на ВП второго
фактора кривая может сильно изменится
(кривые 1 и 2, рис.1).
Для каждого конкретного продуцента и
конкретного ВП необходимо определить количественно эти концентрации (интенсивности)
и выделить их как управляемые переменные, за которыми необходим первостепенный
контроль; найти общий фон прочих питательных веществ и условий культивирования,
обеспечивающих возможность нужного синтеза, как достаточно постоянных
параметров технологического процесса.
Таблица 4.
План ОЭ первого шага, близкий к оптимальному.
|
№э/ф |
1 |
2 |
3 |
4 |
5 |
1-2 |
1-3 |
1-4 |
1-5 |
2-4 |
2-5 |
1-10 |
1-11 |
2-6 |
2-10 |
3-4 |
4-5 |
3-5 |
4-5 |
2-9 |
В у |
|
1 |
1 |
|
|
4 |
|
|
|
8 |
|
|
11 |
12 |
|
|
15 |
|
|
18 |
|
20 |
8 |
|
2 |
1 |
|
|
4 |
|
|
|
8 |
|
|
11 |
12 |
|
14 |
15 |
|
|
18 |
|
20 |
9 |
|
3 |
1 |
|
|
4 |
5 |
|
|
|
9 |
|
|
12 |
|
|
15 |
|
|
|
19 |
|
7 |
|
4 |
1 |
|
3 |
|
5 |
|
7 |
8 |
9 |
10 |
|
|
13 |
14 |
|
|
17 |
18 |
|
|
11 |
|
5 |
1 |
|
3 |
|
5 |
|
7 |
|
9 |
10 |
|
|
13 |
|
|
|
17 |
18 |
|
|
9 |
|
6 |
1 |
|
3 |
4 |
|
|
7 |
|
|
|
11 |
|
13 |
14 |
|
16 |
17 |
|
|
20 |
10 |
|
7 |
1 |
2 |
3 |
4 |
|
6 |
7 |
|
|
|
|
12 |
|
|
15 |
16 |
|
|
|
|
9 |
|
8 |
1 |
2 |
|
|
5 |
6 |
|
|
9 |
10 |
11 |
|
|
14 |
|
16 |
17 |
|
|
20 |
11 |
|
9 |
1 |
2 |
|
|
|
6 |
|
8 |
|
|
|
|
13 |
|
|
16 |
17 |
18 |
19 |
|
9 |
|
10 |
1 |
2 |
|
|
|
6 |
|
8 |
|
|
|
|
13 |
|
|
16 |
|
18 |
19 |
|
8 |
|
11 |
1 |
2 |
3 |
|
5 |
6 |
7 |
|
9 |
|
11 |
12 |
|
14 |
15 |
|
17 |
18 |
|
20 |
14 |
|
12 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
20 |
|
13 |
|
2 |
3 |
4 |
5 |
|
|
|
|
10 |
11 |
|
|
|
|
16 |
17 |
18 |
19 |
|
10 |
|
14 |
|
2 |
|
4 |
|
|
7 |
8 |
9 |
10 |
|
12 |
13 |
14 |
15 |
|
|
18 |
|
20 |
12 |
|
15 |
|
2 |
|
|
5 |
|
7 |
8 |
|
|
11 |
12 |
|
|
15 |
|
|
|
|
|
7 |
|
16 |
|
2 |
3 |
4 |
5 |
|
|
|
|
10 |
|
|
|
|
|
16 |
17 |
18 |
19 |
|
9 |
|
17 |
|
2 |
|
|
|
|
7 |
|
9 |
|
11 |
12 |
13 |
14 |
15 |
|
17 |
18 |
19 |
20 |
12 |
|
18 |
|
2 |
3 |
4 |
|
|
|
|
9 |
10 |
|
12 |
|
14 |
|
|
|
|
|
20 |
8 |
|
19 |
|
|
3 |
|
|
6 |
|
8 |
9 |
10 |
11 |
12 |
13 |
|
15 |
16 |
|
|
19 |
|
11 |
|
20 |
|
|
3 |
|
|
6 |
|
8 |
|
10 |
11 |
|
13 |
|
15 |
16 |
17 |
|
19 |
|
10 |
|
21 |
|
|
3 |
|
|
6 |
|
8 |
|
10 |
11 |
12 |
13 |
|
15 |
|
|
|
19 |
|
9 |
|
22 |
|
|
|
4 |
5 |
6 |
7 |
|
|
|
|
|
|
14 |
|
16 |
|
|
19 |
20 |
8 |
|
23 |
|
|
|
4 |
5 |
6 |
7 |
|
9 |
|
|
|
13 |
14 |
|
16 |
|
|
19 |
20 |
10 |
|
24 |
|
|
|
|
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
14 |
|
|
17 |
|
|
20 |
9 |
После
постановки серии активных экспериментов достаточно провести ранжировку и
выбрать серию опытов с максимальным выходом процесса. Анализируя эти
эксперименты в парах с худшими, несложно
сделать выводы о значимости той или иной группы без явной математической
обработки и арифметических вычислений. При большой ошибке измерения ВП может
быть сложно выбрать единственное
сочетание в первой же серии. Скорее будет найден группа из 2-3 примерно равноценных
экспериментов, недостоверно отличающихся друг от друга по величине ВП. Лучше
сравнивать группы, сильно отличающиеся по выходу процесса, при, желательно,
небольшом качественном различии. Это несложно сделать, представив результаты в
виде корреляционной таблицы, переставляя строки и столбцы первоначального плана
в наиболее удобном и наглядном виде.
После нахождения сильно действующих групп факторов из
разных классов, можно перейти к поиску многокомпонентной синтетической добавки,
уменьшая компоненты неизвестного состава и применяя отсеивающие эксперименты по
сверхнасыщенной схеме для большего количества факторов. В руководстве Максимова, Федорова [2]
приведено много планов, позволяющих проверить влияние факторов при расстановке двух факторов в одном столбце,
размещая каждый фактор на своем уровне (сверхнасыщенность второго типа).
Для
проведения поиска факторов, влияющих на синтез целевого продукта, можно выбрать
план, представленный в таблице 4. В отличие
от обозначений факторов двухуровневых планов, принятых в литературе [1,4]
в виде (+/-), введена нумерация каждого фактора на верхнем уровне и отсутствие
обозначений для нижнего уровня. Номер столбца соответствует новому фактору.
Очень важно, что серия активных
опытов по плану, близкому к оптимальному, позволяет оценить тенденцию влияния того
или иного фактора или комбинации факторов на выход процесса. Это позволяет
более рационально и обоснованно ставить последующие эксперименты.
Обозначение факторов легко увязать с нумерацией столбцов. Упорядоченность расположения факторов в
таб. 6 меньше напрягает внимание и
уменьшает вероятность промаха исполнителем. Это отвечает 0-гипотезе о
наибольшей значимости сочетания факторов
(1,-2) на указанных уровнях. Кроме этого, было увеличено количество
проверяемых факторов путем размещения
на каждом уровне новой добавки (сверхнасыщенность плана поискового эксперимента
2-го типа). Так, в первом столбце поместили пару глюкоза 2г/л – эритрит 2г/л,
т.е. на верхнем уровне - глюкоза, на нижнем - эритрит. Во втором столбце –
фосфат натрия 4 г /л, рН 7,2, на верхнем уровне (ВУ), на нижнем уровне (НУ)-
фосфат той же концентрации, рН 7,8.
Столбец 3 – ВУ гидролизате казеина кислотный 10 г /л, НУ – 5 г /л.
Столбец 4 ВУ аргинин 20 мг/ л, НУ лизин 30 мг/ л. Далее остальные аминокислоты.
На втором этапе, после нахождения
группы активных факторов, можно поставить уточняющий эксперимент по плану
таб.9, построенному на основе ПФЭ 23 по правилу таб.5.
.
Таблица 9.
План второго шага ОЭ на основе ПФЭ 23
|
№э |
|
|
|
1-2 |
1-3 |
2-3 |
3-4 |
К-во верхних уровней в опыте |
Альт столбец 3-4 |
|
1 |
1 |
|
|
|
|
6 |
7 |
3 |
|
|
2 |
1 |
|
3 |
|
5 |
|
|
3 |
7а |
|
3 |
1 |
2 |
|
4 |
|
|
|
3 |
7а |
|
4 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
7 |
|
|
5 |
|
2 |
|
|
5 |
|
7 |
3 |
|
|
6 |
|
2 |
3 |
|
|
6 |
|
4 |
7а |
|
7 |
|
|
3 |
4 |
|
|
7 |
3 |
|
|
8 |
|
|
|
4 |
5 |
6 |
|
4 |
7а |
В таб. 9
условие ортогональности всех вектор - столбцов выполнено, но столбец 7 исходной
таблицы можно заменить на противоположный
(альтернативный) столбец при сохранении ортогональности вектор -
столбцов (равномерному учету пар факторов). Это приведет к потере сочетаний факторов
(1;6;7) и (1;5;7) и некоторых других. Такой план оптимален при наличии информации
об ингибирующем или нейтральном действии указанных сочетаний факторов.
Сочетания (3;4;6), (4;6;7), (5;6;7) присутствуют по 2 раза, что можно учесть
при наличии информации из предварительных экспериментов об их возможной важной
роли. Все возможные варианты рассмотреть сложно и нет смысла в этом. Необходимо производить выбор или построение
плана, близкого к оптимальному, для каждого конкретного случая. Наличие априорной или полученной на первом
этапе информации о сильнодействующих сочетаниях факторов, либо нейтральных по
влиянию на ВП позволяет учесть это и применить планы поиска, оптимальные для
каждого конкретного случая, особенно на последующих, уточняющих этапах поиска.
План табл. 9 построен из ПФЭ 23 по правилу
табл.5. Его так же можно рассматривать как дробную реплику максимальной
дробности от ПФЭ 27. В этом плане учтены все возможные сочетания
факторов по 2 (ортогональность вектор - столбцов) и смещены оценки для
сочетаний факторов высших порядков.
После реализации первого ОЭ возможно, что только в
нескольких экспериментах ВП отличен от 0 и это уже хорошо, т.к. искомое
сочетание факторов попало в проверяемое множество.
Из плана таб.9 можно построить 7! других, заменяя
первоначальные столбцы на их противоположные (альтернативные). Каждый план
будет оптимален для своих начальных условий, по разному смещая частоты учета сочетаний
факторов по 3 и выше.
Первоначальный выбор на проверку группы подозреваемых
факторов и их интенсивностей (концентраций) из очень большого количества потенциально
возможных лежит вне математики, в принципе не формализуем и полностью
определяется интуицией исследователя.
При нахождении небольшой группы сильно действующих
факторов перед постановкой ПФЭ для оптимизации процесса, есть смысл поставить
уточняющую (переходную) серию опытов для экспериментального обоснования выбора
активной группы и их концентраций (интенсивностей), варьируя переменные на 3-х
уровнях по близкому к оптимальности плану таб.10. Как и приведенные выше, план
не единственный, возможны вариации по выбору сочетаний уровней интенсивностей
(концентраций) факторов.
Таблица 9.
План
трехуровневого переходного к оптимизации уточняющего эксперимента.
|
1 |
А1 |
В1 |
С1 |
D1 |
E1 |
|
2 |
А1 |
В3 |
С2 |
D3 |
E2 |
|
3 |
А2 |
В3 |
С3 |
D2 |
E1 |
|
4 |
А2 |
В2 |
С1 |
D3 |
E3 |
|
5 |
А3 |
В1 |
С2 |
D2 |
E3 |
|
6 |
А3 |
В2 |
С3 |
D1 |
E2 |
В плане таб. 9 буквами обозначены факторы, нижними индексами – уровни,
парные сочетания факторов присутствуют с одинаковыми частотами, хотя учтены не
все, теоретически возможные. План не единственный, но близкий к оптимальному согласно
сформулированным выше критериям.
Количество экспериментов в серии в
первую очередь зависит от стоимости каждого опыта. План таб.9. можно расширить
до 8 экспериментов (строк), добавляя эксперименты, в которых все факторы
находятся на одном уровне, т.е. все факторы на 2-ом и все факторы на 3-ем
уровнях. Такое числа испытаний в серии расширение сохраняет учет парных сочетаний факторов, увеличивает
количество учтенных сочетаний факторов и увеличивает представленность сочетаний
факторов более высоких порядков, незначительно смещая частоты представленности
сочетаний факторов более высоких, чем парные, порядков. Наличие трех уровней
варьирования интенсивностей каждого фактора облегчает оценить тенденцию влияния
фактора на ВП. В отличие от двухуровневых планов, наличие трех уровней
варьирования интенсивностей факторов позволяет более точно и надежно оценить
тенденцию по влиянию на синтез ЦП при большой ошибке измерений, что строго
доказано математиками ранее.
Описанный подход был использован для
поиска регуляторных факторов, влияющих на синтез протективного диагностически
важного антигена F41 E/coli и были найдены условия
культивирования , при которых значительно возросло количество названного антигена
в отличии от среды - прототипа [7, 9] .
Поскольку регуляторными факторами выступали совокупности из трех условий
культивирования, найти из в серии однофакторных экспериментов было бы
невозможно.
Заключение
Описанный выше подход основан на минимальном знании
внутренней структуры изучаемого объекта, в первую
очередь генетики и физиологии, и предназначен быть базой как для изучения
(построения) частной физиологии, так и частной генетики живой системы.
Этот подход оперирует в основном контролем внешних условий и измерением реакций
системы, не обязательно с высокой точностью.
Допускается использование качественных
и экспертных оценок, что важно при сложных реакциях мало изученной системы. В ряде случаев можно
обойтись отображением результатов измерений
в виде графиков, корреляционных таблиц и полей при минимуме арифметических
вычислений. По нашему мнению, такой подход может быть применим и к
системам более высокой, чем микробы, организации и более сложным синтезам.
Поскольку ВП в большинстве случаев измеряют с применением химических методов,
то и для чисто химических процессов такой подход тоже применим, особенно для задач
поиска условий кристаллизации.
Литература
1.Максимов В.Н., Федоров В.Д., Применение методов
математического планирования эксперимента при отыскании оптимальных условий
культивирования микроорганизмов. М.,МГУ.,1969., 125 с.
2. Уотсон Дж.
Молекулярная биология гена. М. Мир. 1978. 456 с.
3.Ленинджер А.,Биохимия., М., “Мир”., 1874., 956 с.
4.Стейнер Р., Эдельберг Э., Ингрэм Дж., Мир микробов.,
т.1., М., “Мир” 1979.,320 с.
5.Максимов В.Н., Многофакторный эксперимент в
биологии. М.,МГУ.,1983. 452с.
6.Шулюпин О.К. Критерии оценки оптимальности
отсеивающих экспериментов. Депонированная рукопись. НПО “Медбиоэкономика”
17.11.88. реферат опубликован в библиографическом указателе ВИНИТИ “Депонированные
научные работы” 1989г,№ 3, стр.115.
7.Morris
J.A., Thorng C., Scott A.C., Adhesion in vitro and in vivo associated with an
adhesive antigen (F41) produced by a K99 mutant of the reference strain E.coli B41. Inf. Imm. 1982.v.38. № 3, р.1148-1153.
8.Архипов Г.П., Лаврова И.Г., Трошина И.М.,
Некоторые современные методы статистического анализа в медицине., М.
“Медицина”. 1971., 123 с.
9.Шулюпин О.К., Светоч Э.А., Жиленков Е.Л., Гусев
В.В., Тугаринов О.А., Малахов Ю.А., Питательная среда для выявления
фимбриального антигена адгезии F41. Патент SU
1720652., 23.03.1992 г. Бюл.№11., 4 с.
10.Корн Г., Корн Т., Справочник по математике. М.
“Наука”. ГРФМ. 1984.831с.
Поступила в редакцию
4.10.2011