Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 11. -

Вып. 1. - 2012. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-33-html/TITL-33.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-33-html/cont.htm

УДК 621.396.96

СПОСОБ ПЕЛЕНГАЦИИ ИСТОЧНИКОВ КОГЕРЕНТНОГО ИЗЛУЧЕНИЯ С ИСПОЛЬЗОВАНИЕМ МОДИФИЦИРОВАННОГО МЕТОДА ПРОНИ

Ó 2012 г. Фатов А. В.

(fatov-1.doc)

Пеленгация объектов, представляющих собой сложную систему источников излучения, в условиях присутствия источников излучения когерентных помех представляет собой сложную техническую задачу. Применение модифицированного метода Прони, использующего параметрическую экспоненциальную модель анализируемого сигнала, позволяет получить оценки пеленга геометрического центра лоцируемого объекта в условиях постановки когерентных помех.Приведены результаты имитационного моделирования процесса пеленгации системы, состоящей из двух источников когерентных излучения дополненной источником-эквивалентом фонового излучения, доказывающие работоспособность предлагаемого способа.

Ключевые слова: способ пеленгации, модифицированный метод Прони, когерентные источники излучения

В настоящее время существует класс задач, требующих получения оценок пеленга геометрического центра объекта, представляющего собой сложную систему источников излучения. Локальные источники излучения, входящие в систему объекта следует считать частично когерентными во времени и по пространству. В то же время полностью когерентные (помехи) и некогерентные источники излучения, входящие в систему можно считать частными случаями.

Рассмотрим принцип действия простейшего пеленгатора, например, моноимпульсного типа.В основе его работы лежит предположение о том, что источник излучения точечный. Фазовый фронт волны излучаемой точечным источником представляет собой сферу с центром в точке нахождения источника излучения, поэтому оценкой пеленга точечного источника послужит измеренное значение углового положения нормали к фронту принимаемой волны относительно оси пеленгатора. Для измерения углового положения точечного источника излучения достаточно двух приемных каналов в каждой плоскости пеленгации. Если в диаграмме направленности приемной антенны моноимпульсного пеленгатораприсутствуют нескольких источников излучения, то появляются ошибки оценок пеленга. Величина этих ошибок в общем случае является случайной величиной и будет зависеть от амплитудно-фазовых соотношений между источниками излучений.

В случае когерентности локальных источников излучения, составляющих систему, что соответствует постановке когерентных помех, ошибки пеленгации становятся систематическими.Математическое ожидание ошибок оценки пеленга будет отлично от нуля[1], и будет максимальнов случае, если сигналы излучаемые источниками когерентных помех будут равны по амплитуде и излучаютсяв противофазе.

Получить достоверные оценки пеленга лоцируемого объекта представляющего собой систему источников излучения в условиях когерентных помехвозможно двумя путями. Первым наиболее простым путем является увеличение число приемных каналов. Однако этот путь не всегда рационален, так как увеличение числа точек приема приводит к увеличению массогабаритных характеристик приемной антенной системы, а также увеличивает ее стоимость.Поэтому увеличивая количество приемных антенных каналов, необходимо применять такой способ обработки отсчетов измеренных напряжений на выходе них, который позволяет использовать для своего функционирования наименьшее их количество. Второй путь предполагает собой увеличение числа уравнений в системе уравнений, описывающих многомерное пространство сигналоввточках пространства соответствующих положению антенн [1]. Увеличение числа линейно-независимых уравнений в такой системе уравнений может осуществляться либо за счет использования многоотсчетных алгоритмов обработки принимаемых сигналов, либо с использованием дополнительной корреляционной (функциональной) обработки. Перечисленные способы увеличения количества линейно-независимых уравнений так же имеют свои недостатки, основными из которых являются, увеличение времени выработки оценок пеленга, усложнение конструкции устройства обработки принимаемых сигналов, а также рост объема вычислительных процедур.

Одним из путей решения задачи пеленгации объектов, представляющих собой сложную систему источников излучения, является применение современных параметрических методов цифрового спектрального оценивания, а в частности метода Прони. Одним из его достоинств является эффект сверхразрешения, достигаемый при сравнительно небольших вычислительных затратах.

Метод Прони - один из эффективных методов измерения угловых координат источников сигналов линейной эквидистантной решеткой изотропных антенных элементов [2,3,4]. Он основан на представлении принимаемых сигналов в виде линейной комбинации комплексных экспонент. Каждый источник сигнала характеризуется комплексной амплитудой и комплексной экспонентой, значение которой зависит от угловой координаты источника и номера элемента антенной решетки, на котором сигнал регистрируется.

Суть метода заключается в следующем. Выходной сигнал n-го антенного элемента представляется моделью вида

(1)

где М – количество источников сигналов; a_m – комплексная амплитуда сигнала m-го источника; z_m – комплексная экспонента сигнала m-го источника; d– шаг антенной решетки; l– длина волны; θ_m – угловая координата источника сигнала. Сигналы на выходах всех антенных элементов регистрируются одновременно. Применительно к данной модели последовательность из M отсчетов можно записать в виде системы линейных уравнений, относительно комплексных амплитуд

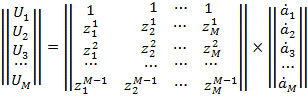(2)

Для решения данной системы используется способ раздельного нахождения неизвестных значений комплексных экспонент z_m, подстановка которых в выражение (2) позволяет определить значения амплитуд . Подход к оценке величины комплексных экспонент основывается на том, что матрица, составленная из их значений в уравнении (1) имеет структуру матрицы Вандермонда и может рассматриваться как решение однородного линейного разностного уравнения с постоянными коэффициентами. Данное линейное разностное уравнение представляет собой полином вида:

, (3)

где коэффициенты полинома заменяются коэффициентами линейного предсказания, которые, в свою очередь, являются решениями систем уравнений, составленных из одновременно измеренных на выходах антенных элементов напряжений. Возможность такой замены базируется на эквивалентности коэффициентов полинома и линейного предсказания:

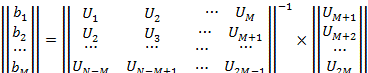(4)

Именно уравнение (4) позволяет получить коэффициенты b_m полинома (3), корни которого принимаются за искомые комплексные экспоненты z_m. Значения комплексных амплитуд экспонент модели вычисляются из системы уравнений (2).

Подробнее остановимся на рассмотрении модифицированного метода, который является самой экономичной разновидностью метода Прони и требует M+M/2 комплексных отсчетов сигнала. Характеристики точности и разрешимости этого метода аналогичны исходному методу [3]. Ввиду минимальных требований к количеству отсчетов принимаемого сигнала необходимых для его работы, данный метод является более предпочтительным, чем выше перечисленные.

Если о принимаемом сигнале известно, что он образован линейной комбинацией незатухающих гармонических сигналов, что обуславливается тем, что структура электромагнитного поля непрерывна как на апертуре, так и за ее пределами и не имеет разрывов, то закономерности формирования поля сохраняются и за пределами апертуры антенны.

Из [2] известно, что уравнение вида (4) для вычисления коэффициентов характеристического полинома (3) может быть сформировано из любых последовательностей отсчетов сигнала размером М. Это утверждение справедливо и для последовательностей отсчетов с отрицательными номерами (относительно первого элемента антенны). Рассмотрим столбец номеров отсчетов от –M до 0 в виде линейного уравнения согласно принятой экспоненциальной модели сигнала (1)

.

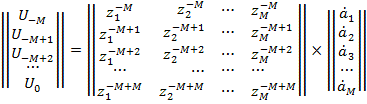Но поскольку z^-1=z^*, то справедливо следующее выражение

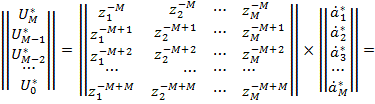
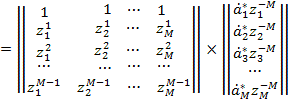, (5)

отличия от (2) будут лишь в столбцах амплитуд. Столбец отсчетов напряжений в выражении (5) представляет собой последовательность комплексно сопряженных отсчетов входных данных.

Поэтому если z_n – незатухающая экспонента с модулем , то любую строку формируемой матрицы исходных данных в (4) можно заменить строкой обратной последовательности комплексно сопряженных отсчетов:

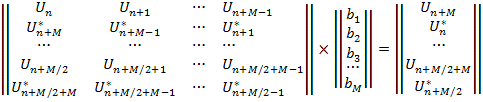. (6)

Уравнение (6) позволяет получить коэффициенты b_mполинома (3), корни которого принимаются за значения искомых комплексных экспонент z_n. По полученным значениям z_n,исходя из модели сигнала (1) можно вычислить значения пеленга θ_m. То есть оценить угловое положение источников сигнала, образующих систему лоцируемого объекта.

Эффективность предлагаемого способа пеленгации объекта представляющего собой систему источников излучения подтверждается результатами имитационного моделирования.

Математическая модель лоцируемого объекта представляет собой систему двух источников когерентных сигналов (сигналов помех) и источника-эквивалента фонового излучения менее интенсивных источников излучения. Источник – эквивалент фонового излучения объекта располагается в точке его геометрического центра, и излучает сигнал, значения амплитуды, которого распределены в соответствии с обобщенным законом Релея, а фаза – равномерно внутри интервала от 0 до 2π. Источники помехового излучения разнесены в пространстве относительно геометрического центра объекта на фиксированное расстояние. Линейная база между источниками помехи равна 25 м. Они являются изотропными и излучают когерентные сигналы равные по амплитуде и сдвинутые по фазе относительно друг друга на π. Истинное значение пеленга на геометрический центр объекта принято равным α₀ = 30°. Угловая база между источниками помехового излучения ∆α принималась равной 0,1; 0,3; 0,5 ширины главного лепестка диаграммы направленности пеленгатора. В соответствии с величиной угловой базы изменялось текущее значение дальности между объектом и пеленгатором. Исходная величина отношения мощностей помехового и фонового излучения 45 дБ. Значения величин амплитуд помехового и фонового излучения сигналов, принимаемых пеленгатором, изменялись в соответствии с текущим значением дальности между ним и лоцируемым объектом.

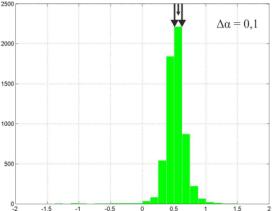
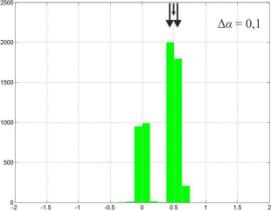
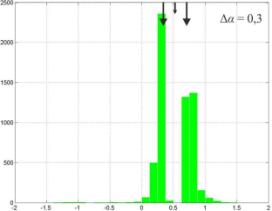
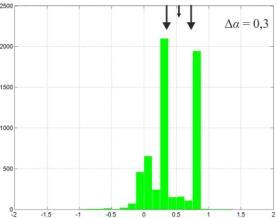
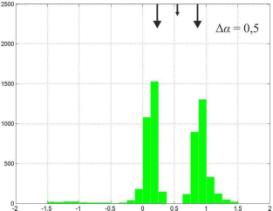
Результаты имитационного моделирования представлены на рисунке1, на котором изображены гистограммы распределения оценок пеленга на источники помехового и собственного излучения. Положения источников излучения, соответствующие истинному значению пеленга обозначены стрелками. Левая колонка результатов соответствует использованию трех приемных каналов, правая – пяти соответственно.

Из рисунка1 видно, что в случае, когда источники сигналов не разрешаются (величина угловой базы между источниками помехового излучения равна 0,1 ширины главного лепестка антенны), выдается оценка лоцируемого объекта соответствующая его геометрическому центру.

Пеленгатор, использующий три приемных канала при наличии базы между источниками сигналов когерентных помех ∆α ≥ 0,3 ширины главного лепестка антенны, вырабатывает оценки пеленга соответствующие доминирующим источникам сигналов (сигналов помех).

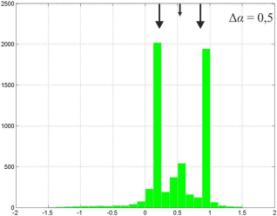
Использование пеленгатором пяти приемных каналов при наличии базы между источниками сигналов помех ∆α ≤ 0,3 ширины главного лепестка антенны приводит к тому, что вырабатываются ложные оценки пеленга. Это объясняется тем, что для указанных выше значений величины угловой базы (на соответствующих дальностях) все три источника излучения сигналов не разрешаются. Из [3,4] известно, что при выборе больших порядков предсказания (порядок модели больше, чем количество сигнальных составляющих) наряду с истинными значениями оценок появляются шумовые, что влечет за собой проблему последующего отделения истинных и ложных оценок измеряемого параметра. При увеличении величины угловой базы между источниками когерентных сигналов ∆α ≥ 0,3 пеленгатор использующий пять приемных каналов вырабатывает оценки всех трех источников сигналов, составляющих систему постановщика когерентных помех.

Рисунок1 – Гистограммы распределения оценок в зависимости от величины угловой базы и использовавшегося количества приемных каналов

Анализируя результаты имитационного моделирования (рисунок 1) можно сделать следующие выводы:

1. В случае если все три источника сигналов составляющих систему источников излучения лоцируемого объекта не разрешаются, пеленгатор как в случае использования трех, так и пяти приемных каналов вырабатывает значения равные и близкие положению его геометрического центра.

2. В случае отсутствия априорной информации о составе системы источников излучения составляющей лоцируемый объект использование большего количества приемных каналов, чем необходимо для реализации способа, приводит к появлению ложных оценок пеленга отдельных источников излучения ∆α ≤ 0,3. Полученные при этом оценки находятся за контуром лоцируемого объекта. Использование же меньшего количества каналов приводит к тому, что вырабатываются оценки пеленга доминирующих источников излучения, что не снижает возможности определения углового положения геометрического центра лоцируемого объекта.

Литература

1. Царьков Н. М. Многоканальные радиолокационные измерители. М., Сов.радио, 1980. 256 с.

2. Марпл-мл С. Л. Цифровой спектральный анализ и его приложения. – М.: Мир, 1990. 342 с.

3. Савинов Ю. И. Метод Прони: моногр. – Смоленск, изд. ВА ВПВО ВС РФ, 2007. 74с.

4. Абраменков В. В. Измерение координат радиолокационных целей методами многосигнальной радиолокации. Монография. Смоленск: ВУвойсковойПВОВСРФ, 2002.

DIRECTION FINDING METHOD OF SOURCES OF COHERENT RADIATIONUSING A MODIFIEDPRONY'S METHOD

Fatov A.

A direction-finding of object represented as a complex system of sources of radiation in the presence of radiation sources of coherent noise is a technical challenge. Application of the modified Prony method that uses a parametric exponential model of the analyzed signal allows obtaining estimates of bearing geometric center of located object in a coherent gamming. The results of simulation of the process of direction finding system consisting of two sources of coherent radiation source, supplemented with the equivalent background radiation, demonstrating the efficiency of the proposed method are adduced.

Key words: direction finding method, the modified Prony's method, coherent radiation sources.

Военная академия войсковой ПВО Вооруженных Сил Российской Федерации

имени Маршала Советского Союза А.М. Василевского

(ВА ВПВО ВС РФ)

Поступила в редакцию 21.02.2012.