Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 11. -
Вып. 1. - 2012. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-33-html/TITL-33.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-33-html/cont.htm
УДК 57.017.6
Старение живых организмов
Ó
2012 г. Седова Г. П.
Все организмы
– как одноклеточные, так и многоклеточные, с возрастом замедляют свой рост и
стареют. Но у одноклеточных организмов после митоза потенциал роста восстанавливается, а у многоклеточных – нет.
Поэтому, популяции свободно живущих одноклеточных организмов удваивают свою
массу с постоянным временем, т. е. не стареют. Многоклеточные же организмы, являющиеся
популяциями связанных между собой клеток, с возрастом замедляют свой рост и
стареют. Математический анализ имеющихся
экспериментальных данных по количественному росту многоклеточных организмов
позволяет сделать вывод о том, что каждое удвоение массы многоклеточного
организма связано с потерей k-ой части его
начального потенциала. Здесь k – параметр,
показывающий скорость старения организма.
Ключевые
слова: старение одноклеточных, старение многоклеточных организмов.
Содержание
1.
Общие сведения о
старении живых организмов
2.
Старение одноклеточных
3.
Старение многоклеточных
Общие сведения о старении живых организмов
Все живое на Земле стареет и умирает. Стареют и
отмирают отдельные клетки и целые организмы, животные и растения.
В чем причина старения? Можно ли замедлить этот процесс
и отодвинуть смерть? Эти вопросы с
давних времен волновали людей.
Над ними думали многие известные представители
медицинской науки.
В настоящее время отношение ученых к проблеме старения
и смерти двойственное. Одни из них с легкостью обещают нам бессмертие, т. е. вечную
жизнь, причем в самом недалеком будущем. Другие утверждают, что бессмертие
недостижимо и что предельный возраст человека 125 лет.
«Геном человека расшифрован, путь к бессмертию открыт»
- бодро восклицают одни.
Другие, более сдержанные, говорят о том, что этот
проект нисколько не приблизил нас к
тайне жизни, и ничего не дал для практики.
Надежда, если не на бессмертие, то, по крайней мере,
на увеличение продолжительности жизни появилась когда было открыто, что с возрастом
длина концевых участков хромосом – теломер укорачивается. Было установлено, что
у одноклеточных организмов есть фермент – теломераза, который восстанавливает
укороченные участки хромосом. Этого фермента нет у многоклеточных организмов.
Ученые надеялись с помощью этого фермента увеличить продолжительность жизни
человека.
Но оказалось, что вмешательство в клетки
многоклеточного организма с помощью теломеразы чревато злокачественным ростом
клеток. Хотим мы такого бессмертия? Конечно, нет.
Специалисты также выражают беспокойство по поводу
использования стволовых клеток, вокруг которых сейчас так много сенсаций. Нет
уверенности в том, что они также не могут провоцировать рак.
Похоже на то, что Природа жестоко наказывает за всякое
вмешательство в живой организм с целью увеличения продолжительности его жизни.
Необходимо также иметь в виду, что результаты по увеличению
продолжительности жизни отдельной клетки невозможно распространить на многоклеточный
организм. Можно сказать, что на уровне одноклеточного организма указанная
проблема давно решена, и решена довольно просто. Для этого достаточно отрезать
от него часть массы и не доводить его до митоза. Так, немецкий зоолог М. Гартман 64 раза отрезал у амебы часть ее
тела, которая успешно восстанавливалась. Тем самым продолжительность жизни
амебы многократно увеличивалась.
Но если мы то же самое проделаем с многоклеточным
организмом, то мы его искалечим, нисколько не продлив ему жизнь.
Еще один способ биологического продления продолжительности
жизни связан с периодическим
ограничением питания или полным лишением пищи живого организма. Это направление опирается на работы профессора
военно-медицинской академии В. В. Пашутина. Они относятся к концу 19-го и началу
20-го века. В. В. Пашутин проделал большое количество опытов над животными и
пришел к выводу о том, что лечебное голодание замедляет старение и продлевает
жизнь голодающих животных по сравнению с регулярно питающимися особями. Сейчас
за давностью уже затруднительно найти в литературе описание этих опытов.
Но удивляет повторяющаяся в некоторых статьях,
посвященных проблеме долголетия, фраза, что путем лечебного голодания «например,
можно продлить жизнь дождевым червям в 19 раз, мышам в 4 раза, а высокоразвитым
крупным млекопитающим в 1,5-2 раза». Вот, оказывается, как, по мнению подобных
авторов, все обстоит просто. Уверена, что никаких подобных выводов из своих
опытов профессор Пашутин не делал. Это
последующие авторы произвольно их истолковали.
Вообще, литература, посвященная продолжительности
жизни живых организмов, поражает своими необоснованными, безответственными выводами.
Авторы порой сами не отдают себе отчета, о какой продолжительности жизни они
ведут речь: о максимальной видовой продолжительности жизни животного, о средней
видовой продолжительности или о времени хозяйственного использования данного
вида животных.
Вот, например, в одной из статей читаем, что биолог
Сурен Аракелян с применением физиологически полезного голодания увеличил
продолжительность жизни коров в 3 раза. Возникает вопрос: какую продолжительность
жизни коров увеличил экспериментатор? Явно, не максимальную, которая у коров
составляет 20-25 лет. (См., напр. Сб. ст. «Биология старения» Л., Наука, 1982 г.).
А по некоторым источникам она составляет 30 лет. Если бы речь шла о
максимальной продолжительности жизни, то экспериментатору нужно было бы
наблюдать этих коров, по крайней мере, в течение 20х3 = 60 лет. Так о какой продолжительности
жизни идет речь? О средней? Тогда нужно указать, какова она у коров. Может
быть, речь идет о той продолжительности жизни, которая отведена корове от
момента ее рождения до того времени, когда ее сдадут на мясокомбинат? Но
последняя не зависит ни от каких других причин, кроме желания хозяина.
Вернемся к ранее упомянутым дождевым червям, которым с
помощью того же голодания экспериментаторы увеличили продолжительность жизни аж
в 19 раз. По разным источникам, максимальная продолжительность жизни дождевых
червей составляет 4-10 лет. В этом случае эксперимент должен был длиться 4х19 =
76 лет.
Приведенные примеры свидетельствуют о том, что никакой
строгости суждений в подобных публикациях нет, и они не могут приниматься в качестве
доказательства преодоления максимального видового предела продолжительности
жизни живого организма.
Если распространить метод продления жизни путем
периодического голодания на человека, то думаю, что мало найдется желающих
вести полуголодную жизнь ради того, чтобы увеличить ее на несколько лет.
Правда, С. Аракелян утверждает, что путем периодического
голодания можно продлить жизнь человека до 300-500 лет. Хорошо было бы, если бы
авторы подобных утверждений демонстрировали их на собственном организме.
Изучением
процесса старения живых организмов занимается медико-биологическая наука – геронтология. Выводы, к которым
пришли выдающиеся геронтологи мира следующие: увеличение максимальной продолжительности
жизни человека является нереальной задачей.
Реально только увеличение средней продолжительности
жизни, как следствие того, что все большее количество людей будет доживать до
максимального видового предела продолжительности жизни человека. Но в экономически
развитых странах фактически исчерпан резерв
увеличения средней
продолжительности жизни за счет дополнительных социальных преобразований.
Понятно, что Россия к таким странам не относится.
Время от времени в научно-популярных журналах
появляются статьи с названиями типа «Таблетка от старости», «Генетики
приблизили бессмертие человека», «Подредактировав ДНК, человек сможет жить до
800 лет» и т. д.
Выдающийся британский геронтолог Робин Холлидэй задает
вопрос:
«Как можно делать такие заявления?».
«Все это движение против старения не только
превращается в научную фантастику, но и является поразительной наглостью».
Р. Холлидэй считает, что громадное количество
опубликованных исследований по старению живых организмов указывает на то, что
смерть человека в возрасте 125 лет неизбежна. Такой вывод согласуется с реальностью.
Супердолгожителями являются люди в возрасте 110-120 лет. Разумеется, речь идет
только о тех случаях, когда возраст подтвержден документально.
Природа установила для каждого вида живых существ
максимальный предел продолжительности жизни, преодолеть который ни одно
существо данного вида не может.
По-видимому,
125 лет – это максимальный предел продолжительности жизни человека,
которого достигают лишь отдельные представители человеческой популяции.
Не все ученые согласны с таким выводом. И если есть
те, кто считают, что способны одарить людей бессмертием, то пожелаем им всяческих
успехов. Как хорошо заметил корреспондент одной газеты в беседе с одним из
таких ученых - бессмертие бы нам не помешало. Но нельзя выдавать желаемое за
действительность.
Старение одноклеточных
В качестве основного аргумента в пользу возможности достижения
бессмертия его сторонниками приводится факт о якобы имеющем место бессмертии в
мире одноклеточных. Отсюда делаются далеко идущие выводы, а именно: если одноклеточные
организмы бессмертны, то смерть живых существ вовсе не запрограммирована
Природой, следовательно, ее можно обойти и что человек со временем может достигнуть бессмертия.
Но представление о бессмертии одноклеточных организмов
является ошибочным и исходит из того, что в литературе по одноклеточным организмам
происходит постоянная путаница вокруг двух разных понятий, а именно, продолжительности
жизни одноклеточного существа как индивидуума, как отдельной особи, и
продолжительности существования популяции одноклеточных организмов.
Жизнь одноклеточного организма продолжается от митоза
до митоза. За этот период одноклеточный организм растет, стареет и умирает. Но
для него процесс смерти и процесс размножения совпадают.
Воспользуемся экспериментальными данными акад. И. И.
Шмальгаузена по росту бактерии Micrococcus . (1926г.). Необходимо подчеркнуть, что речь идет не о
том, как растет популяция этих бактерий, а о том, как увеличивается с течением
времени масса одной не видимой невооруженным глазом бактерии. Бактерия эта
имеет шарообразную форму. Измерялся ее диаметр через каждые 6 минут. По
диаметру мы можем найти объем, массу будем считать пропорциональной объему.
Произведя необходимые вычисления, заполним таблицу.
Рост бактерии Micrococcus в бульон-пептон агаре
|
Время, минуты |
Диаметр, микроны |
Объем, микроны кубические |
Прирост объема, микроны кубические |
|
0 |
1,360 |
1,317 |
|
|
6 |
1,440 |
1,564 |
0,247 |
|
12 |
1,506 |
1,787 |
0,223 |
|
18 |
1,559 |
1,981 |
0,194 |
|
24 |
1,609 |
2,178 |
0,197 |
|
30 |
1,658 |
2,361 |
0,183 |
|
36 |
1,687 |
2,51 |
0,149 |
|
42 |
1,717 |
2,647 |
0,137 |
|
48 |
1,744 |
2,778 |
0,131 |
|
54 |
1,765 |
2,885 |
0,107 |
|
60 |
1,790 |
3,004 |
0,119 |
Рассматривая эту таблицу, мы видим, что прирост объема
( массы) бактерии за равные промежутки времени ( 6 минут ) в течение ее жизни
уменьшается, т. е. бактерия замедляет свой рост, стареет, причем наибольший прирост
массы происходит непосредственно после митоза в самом начале роста. В самом
конце роста, перед следующим митозом имеет место некоторое увеличение скорости
роста, я не знаю, как это объяснить.
Замедление роста является признаком старения
организма, оно свидетельствует о замедлении процессов биосинтеза в клетке.
Такая же закономерность прослеживается при анализе
роста двух других одноклеточных
организмов – дрожжевой клетки и парамеции.
Экспериментальные
данные акад. И. И. Шмальгаузена.
Рост дрожжевой клетки
Измеряли каждый раз длину и ширину, по которым
выводили среднюю величину l . По
изменению этой величины будем судить о скорости роста дрожжевой клетки
|
Время, минуты |
Средняя величина l ,
микроны |
Прирост средней величины, микроны |
|
20 |
13,7 |
|
|
40 |
31,06 |
17,36 |
|
60 |
42,83 |
11,77 |
|
80 |
51,53 |
8,7 |
|
100 |
57,15 |
5,62 |
|
120 |
61,14 |
3,99 |
|
140 |
64,24 |
3,1 |
|
160 |
66,63 |
2,39 |
|
180 |
68.03 |
1,4 |
|
200 |
70,57 |
2,54 |
Рост парамеции
Бактерия растет в длину. Поэтому объем
пропорционален длине.
|
Время часы |
Длина микроны |
Прирост
длины за каждые 3 часа, микроны |
|
0 |
175 |
|
|
1 |
215 |
|
|
2 |
230 |
|
|
3 |
235 |
60 |
|
6 |
250 |
15 |
|
9 |
260 |
10 |
|
12 |
265 |
5 |
|
15 |
270 |
5 |
|
18 |
275 |
5 |
Некоторые
авторы считают, что при размножении одноклеточных нет трупа, а следовательно,
и нет смерти материнской особи. Но специалистами доказано, что при этом
процессе имеют место трупные явления, т. к. происходит гибель части живой
материи.
Т. о., никакого бессмертия в мире одноклеточных
организмов нет. Относительно бессмертны только их популяции, но не отдельные
особи. Об этом хорошо сказано, например, в сборнике «Биология старения» (Л. «Наука»,
1982 г., раздел – Старение и смерть одноклеточных). Говорить о бессмертии
одноклеточных также неправомерно, как утверждать, что человек бессмертен, на
том основании, что в человеческой популяции происходит постоянная смена
поколений. Относительно бессмертна (пока есть условия для ее существования)
человеческая популяция, но каждый человек смертен.
Старение
многоклеточных организмов
Многоклеточный организм, в сущности, представляет
собой клеточную популяцию, но в отличие от популяции независимых друг от друга
клеток, эти клетки связаны между собой в единую массу.
Промежуточные положения, когда одноклеточные после
митоза, могут объединяться в отдельные группы или колонии, здесь не рассматриваются.
Сравним по характеру роста популяцию свободно живущих
одноклеточных организмов и многоклеточный организм.
Популяция одноклеточных, в условиях полного
обеспечения питанием и отвода вредных продуктов жизнедеятельности, удваивает
свою массу с постоянным периодом, т. е. она не замедляет роста и не стареет на
протяжении жизни многих поколений клеток, в среднем порядка нескольких тысяч
поколений. Это экспериментально установленный факт. Т. о., можно сказать, что
потенциал роста популяции одноклеточных организмов ( но не отдельной особи ) не
снижается с течением времени.
В то время как многоклеточный организм, представляющий
собой также клеточную популяцию, замедляет рост, т. е. стареет с самого начала
роста, т. е., его потенциал роста снижается с возрастом. И это также экспериментально
установленный факт.
Акад. И. И. Шмальгаузен установил, что рост куриного
эмбриона замедляется уже после 2-х суток насиживания.
Можно доказать, что снижение потенциала роста многоклеточного
организма подчинятся строгой математической зависимости.
Для этого я очень коротко повторю вывод из своей ранее напечатанной работы «Закономерность
роста биологических объектов» («Математическая морфология», 2004 г.).
Рассматриваем многоклеточный организм, как единое
целое и поставим перед собой задачу установить закономерность нарастания его
массы с возрастом.
Возьмем за характеристику скорости роста время,
необходимое для удвоения массы живого организма. Воспользуемся имеющимися в литературе
экспериментальными данными по росту. Вычислим указанное время, соответствующее
разному возрасту живого организма, обозначим его a = f ( t ). Разумеется, экспериментальные данные должны быть достаточно
точными. Никакие приближенные данные не могут быть использованы, т. к. они
дадут искаженные результаты. Построим графики
a = f ( t ) для разных организмов. Эти графики для всех
организмов представляют собой прямую линию.
Это означает, что время,
необходимое для удвоения массы живого организма с его возрастом увеличивается
по линейному закону. В виде
формулы это выглядит следующим образом:
a = a0
+ kt ,
где
a0 -
начальный период удвоения массы
k - коэффициент
замедления роста.
a0 и k - параметры, постоянные для каждого организма на всем
протяжении его роста, но разные для разных организмов.
Отсюда получается формула массы многоклеточного
организма, соответствующая его возрасту t :
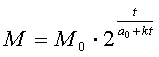 ,
,
где
M0 -
начальная масса организма.
Как частный
случай этой формулы получаем формулу
для массы популяции одноклеточных:
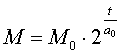 .
.
Введем величину, обратную времени удвоения массы, обозначим
ее q и назовем потенциалом
роста q= ![]() . Ясно, что чем
время удвоения массы меньше, тем потенциал роста больше, и наоборот.
. Ясно, что чем
время удвоения массы меньше, тем потенциал роста больше, и наоборот.
Начальный потенциал роста живого организма заложен в
зиготе. Обозначим его q0 = ![]() . Это максимальный потенциал, в процессе
роста он будет только уменьшаться.
. Это максимальный потенциал, в процессе
роста он будет только уменьшаться.
Поставим перед собой задачу: опираясь на полученную
нами ранее эмпирическую формулу a = a0 + kt установить, как изменяется потенциал роста в зависимости от числа удвоений, т. е.
получить формулу q = f ( n ) ,
где n - число удвоений массы.
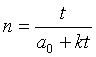
Откуда 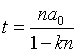
a = a0 +kt
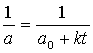 .
.
Подставив в эту формулу ранее полученное выражение для
t
, после некоторых преобразований,
получим:
![]() .
.
Последняя формула означает, что на
каждое удвоение массы многоклеточного организма расходуется k-ая часть
его начального потенциала роста. Число
удвоений n может быть дробным, это означает, что
удвоилась не вся масса организма, а какая-то его часть.
Т. о., в многоклеточном
организме с каждым удвоением массы потенциал роста закономерно снижается, и, в
конце концов, исчерпывается полностью.
Поэтому, правы те авторы, которые считают старение и смерть многоклеточных организмов
« платой за многоклеточность ».
И. И. Шмальгаузен писал по этому поводу: «Строгая
закономерность его (падения скорости роста) свидетельствует о каком-то изменении
во внутреннем равновесии системы, вероятно, в изменениях тончайшей структуры
самого живого вещества, что связано с самим существованием организма. Рост
наталкивается на какое-то препятствие, увеличивающееся пропорционально времени
».
Выдающийся биолог Э. С. Бауэр (1980-1938) считал, что
существование живого вещества связано с особым, неравновесным состоянием молекул белка.
«Только живые системы никогда не бывают в равновесии и
исполняют за счет своей свободной энергии постоянно работу против равновесия,
требуемого законами физики и химии при существующих внешних условиях».
Рост же популяции свободно живущих одноклеточных организмов
происходит иначе. Потенциал роста такой популяции от поколения к поколению не
уменьшается, остается постоянным. Как мы видели, для каждой особи в течение
интерфазы потенциал роста снижается. Но после митоза, каким – то образом он
восстанавливается вновь, т. е. дочерние клетки получают тот же потенциал,
который имела материнская клетка в начале роста. Если бы это было иначе, то популяция
не удваивала бы свою массу с постоянным временем.
Возникает аналогия между установленным различием в
закономерности роста многоклеточных и одноклеточных организмов и аналогичным поведением теломер этих организмов.
Установлено, что в клетках многоклеточных организмов теломеры укорачиваются и
не восстанавливаются. У одноклеточных же они восстанавливаются.
На вопрос: есть ли связь между укорочением теломер и
закономерностью роста живых организмов, математика дать не может. Она только
устанавливает количественные закономерности.
Как справедливо утверждал акад. Н. П. Дубинин «Математика
является лишь методом, который отнюдь не компетентен в деле обнаружения самой
сущности явлений».
Последнее
слово всегда за экспериментом и правильным его истолкованием.
Литература
1.
Биология старения. Сб.
ст. – Л: Наука,1982. - 616с.
2.
Догель В. А. Общая
протистология. - М: Советская наука, 1951.
– 603 с.
3.
Седова Г. П.
Закономерность роста биологических объектов. // Математическая морфология. – 2004, - Вып. 2.
4.
Шмальгаузен И. И. Рост и
дифференцировка. Т. 1 – Киев: Наукова Думка, 1984. – 176 с.
5.
Шмальгаузен И. И. Рост и
дифференцировка. Т. 2. – Киев: Наукова Думка,1984. – 168 с.
Aging live organisms of
Sedova G. P.
All organisms – both monocelled, and
multicellular, slow down with the years the growth and grow old. But at
unicells after a mitosis the growth potential is restored, and at multicellular
– isn't present. Therefore, populations of freely living unicells double the
weight with constant time, i.e. don't grow old. The multicellular organisms
which are populations of cages connected among themselves, slow down with the
years the growth and grow old. The mathematical analysis of available
experimental data on quantitative growth of metaphytes allows to draw a conclusion
that each doubling of weight of a metaphyte is connected with loss k – oh parts
of its initial potential. Here k –
the parameter showing speed of aging of an organism.
Key words: aging monocelled, aging of metaphytes.
Орел. Пенсионерка.
Поступила в редакцию
6.12.2011