Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 11. -

Вып. 2. - 2012. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-34-html/TITL-34.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-34-html/cont.htm

 

 

УДК 681.3.001.57

 

ПРОГНОЗИРОВАНИЕ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ НА ОСНОВЕ МЕТОДА ГЛАВНЫХ КОМПОНЕНТ

 

Ó 2012 г. Волосенков А. В.

 

(volosenkov-1.doc)

 

Рассматривается задача прогнозирования многомерного временного ряда на основе метода главных компонент. Предложенный метод базируется на сингулярном разложении траекторной матрицы, столбцами которой являются вектора вложения – отрезки ряда равные длине окна. Метод позволяет построить рекуррентный прогноз многомерного ряда, не требуя предварительного задания модели ряда, и демонстрирует лучшие результаты, чем применение одномерного метода к рядам по отдельности.

Ключевые слова: многомерный временной ряд.

 

Одной из главных задач в теории временных рядов является вычисление прогнозных значений исследуемого временного ряда. В настоящее время существует множество различных методов прогнозирования временных рядов, но ни один из них нельзя называть универсальным или лучшим. Причиной этого является уникальность исследуемых процессов, а именно скрытая зависимость элементов временного ряда между собой. Большинство эконометрических методов анализа и прогнозирования временных рядов базируется на заранее принятых гипотезах о классе функциональных зависимостей, среди которых ведется поиск наилучшей. Это обстоятельство не позволяет утверждать однозначно, что построенная эконометрическая зависимость является действительно наиболее эффективной. Указанный недостаток полностью отсутствует при анализе многомерных временных рядов при помощи метода главных компонент. Особенности анализа многомерного временного ряда на основе метода главных компонент, а также его преимущества перед одномерным анализом уже были рассмотрены в [1]. Численные эксперименты подтверждают, что если ряды имеют похожую структуру, то прогноз, основанный на рассматриваемом методе, является более точным и имеет меньшие показатели средней квадратической ошибки по сравнению с применением одномерного метода главных компонент к рядам по отдельности.

Пусть наблюдается система из  временных рядов равной длины

,

где . Параметр  есть длина ряда. На этапе сингулярного разложения траекторной матрицы данного ряда при анализе многомерного временного ряда с помощью метода главных компонент [1] получаем  – ортонормированную систему собственных векторов  - матрицы вторых моментов полученной многомерной выборки, соответствующих собственным числам  матрицы , взятым в порядке убывания .

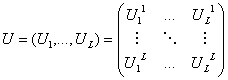
Введем следующие обозначения:

пусть , где , и

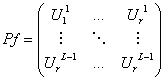
Рассмотрим следующую систему уравнений:

 (1)

Так как , то система (2.9), вообще говоря, несовместна, хотя и существует широкий класс функций, для которых она разрешима. Расширим понятие решения системы (1).

Обобщенным решением системы (2.9) назовем решение системы

 (2)

Очевидно, система уравнений (2) разрешима, если матрица  имеет ранг .

Пусть  есть решение системы уравнений (2). Тогда продолжением ряда  объявляется число

 (3)

Из общей теории решения линейных систем следует, что общее решение (2) может быть записано в виде:

где  - обобщенная обратная матрица к матрице , а  - произвольный вектор. Очевидно, обобщенное продолжение будет единственно, если . Следующая теорема дает критерий единственности обобщенного продолжения функции дискретного аргумента.

Теорема. Условие

 (4)

является необходимым и достаточным для единственности обобщенного продолжения ряда  [2].

Условие (2.12) может быть записано в следующем виде:

 (5)

Матрица , входящая в равенство (5), есть не что иное, как матрица Грамма системы векторов . Если эта система векторов линейно независима, то , и  обратима в обычном смысле. В этом случае равенство (5) тривиальным образом выполняется. Таким образом, справедлива следующая лемма.

Лемма. Для однозначного продолжения функции  достаточно, чтобы система векторов  была линейно независима.

Заметим, что в качестве сомножителя  в правой части системы (1) вместо первых  компоненты последнего столбца матрицы данных исходного ряда могут быть взяты соответствующие компоненты матрицы данных продолженного ряда. Это обстоятельство позволяет после вычисления по формуле (3) продолжить вычисление по этой же формуле следующих элементов ряда .

 

Литература

 

1.  Волосенков А.В. Анализ многомерных временных рядов на основе метода главных компонент.

2.  Главные компоненты временных рядов: Метод «Гусеница». Ред. Данилов Д.Л., Жиглявский А.А. Санкт-Петербург, СПбГУ, 1997]

 

 

FORECASTING MULTIVARIATE TIME SERIES BASED ON PRINCIPAL COMPONENT ANALYSIS

 

Volosenkov A.V.

 

The problem of forecasting multivariate time series based on principal component analysis. The proposed method is based on singular value decomposition trajectory matrix whose columns are the vector of embedding - a number of segments of equal length windows. The method allows one to construct a recursive multivariate prediction series, without requiring to specify the model of time series and shows better results than using the one-dimensional method to the series separately.

Key words: multivariate time series.

 

ФГБОУ ВПО «Национальный исследовательский университет «МЭИ»  в г. Смоленске»

Smolensk Branch of National research university

«Moscow Power Engineering Institute»

Поступила в редакцию 25.04.2012.