Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 11. -
Вып. 3. - 2012. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-35-html/TITL-35.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-35-html/cont.htm
УДК 536-33+536-34+536.78
КРИТИЧЕСКИЕ ПАРАМЕТРЫ И КРИТИЧЕСКИЕ ЯВЛЕНИЯ
Ó 2012 г.
Конов А.Ф.
В статье показывается, что определение критических
параметров по моменту исчезновения мениска приводит к возникновению неразрешимых
проблем, вызванных тем, что в критической точке термометр измеряет не
температуру газа в колбе, а температуру термостата.В критической точке
температура термостата в три раза выше, чем температура газа в колбе.
Приводится описание способа определения критических параметров с использованием
PV,P-диаграммы. Сравнение критических параметров, полученных двумя
способами, показывает, например, что 
и 
в критическом
состоянии это кажущеюся теплоемкости. Здесь тепловую энергию, необходимую для
увеличения уровня температуры в 2 раза превышающую критическую температуру газа,
ошибочно принимают за энергию необходимую для нагрева реального газа на 1K.
Согласование критических параметров, определенных по новому способу, с
физическими свойствами газа, наблюдаемые в различных процессах, создает
совокупность теории и эксперимента, которая не допускает возникновения ошибок.
Ключевые слова: тепловое
излучение, длина волны, максимум спектра излучения, формула Планка, закон
смещения Вина, давление излучения в замкнутой полости.
Данная
статья является продолжением описания работы теплового насоса [1] и статьи об
ошибке в теории теплового излучения [2].
Каждую
из этих статей, включая данную статью, можно считать отдельной и законченной
работой и, тем не менее, вместе они создают неразрывную совокупность доказательной
базы физического обоснования принципа работы теплового насоса с максимальным
отопительным коэффициентом.
В
новом тепловом насосе в качестве рабочего тела используется реальный газ, который
в начале цикла приводится в критическое состояние. Данное требование является необходимым
условием для получения максимального
отопительного коэффициента теплового насоса. Отсюда следует, что определение
критических параметров является одним из основных требований при решении практических
задач.
При
описании ошибки в теории теплового излучения отмечается, что плотность энергии
излучения в замкнутой полости (полость без отверстия) в 
раз превышает плотность излучения в световом потоке. В
предлагаемой статье предполагается, что кривая Бойля PV, P – диаграмме образуется в
результате давления теплового излучения на атом газа. Кроме того, в данной
статье приводится описание нового способа определения критических параметров
веществ по состоянию реального газа далекому от критической точки. И, наконец,
приводятся примеры согласования полученных значений критических параметров с
работой теплового насоса, эффектом Джоуля-Томсона и критическими явлениями.
В
настоящее время определение критических параметров веществ производится по
моменту исчезновения мениска в процессе нагревания вещества в герметически
закрытой колбе [3].
В этом
способе считается, что если закрытая колба с веществом помещена в термостат с
определенной температурой, то естественно, что и температура вещества в колбе
имеет температуру термостата. Такое предположение для критического состояния
приводит к возникновению неустранимых противоречий. Существование этих
противоречий приводит к необходимости введения отдельного рассмотрения
критических параметров и критических аномальных явлений. Примером таких аномальных
явлений в критической точке можно назвать изохорную теплоемкость 
. Из этого равенства следует, что подведенная теплота 
может быть бесконечно большой, при этом разность
температур всегда равна нулю, т.е. температура газа не изменяется при подводе неограниченного
количества энергии.
Как
отмечается в [4 c.173] « Из известных термодинамических соотношений
вытекает, что теплоемкость при постоянном давлении в критической точке,
бесконечно велика…».
Таким
образом, в критической точке при подведении неограниченной тепловой энергии
параметры газа 
, 
, 
не изменяются.
Возникает вопрос: На что расходуется подведенная энергия? Если эта энергия
исчезает бесследно тогда, как быть с фундаментальным законом сохранения
энергии?
Эта
проблема известна более 100 лет и конечно существуют различные теории, объясняющие
это явление. Одна из наиболее популярной является теория флуктуации.
Однако ни одна теория не может объяснить
существование реального процесса в газе на поддержания, которого требуется
бесконечная энергия.
Характер
противоречий отмеченных при описании состояния газа в критическом состоянии
требует изменения точки зрения на свойства газа, которые определяются не только
движением атома в целом, но и взаимодействием электронов с его ядром.
Формула
Борна-Опенгейнера позволяет вычислить энергию электронов, считая неподвижным
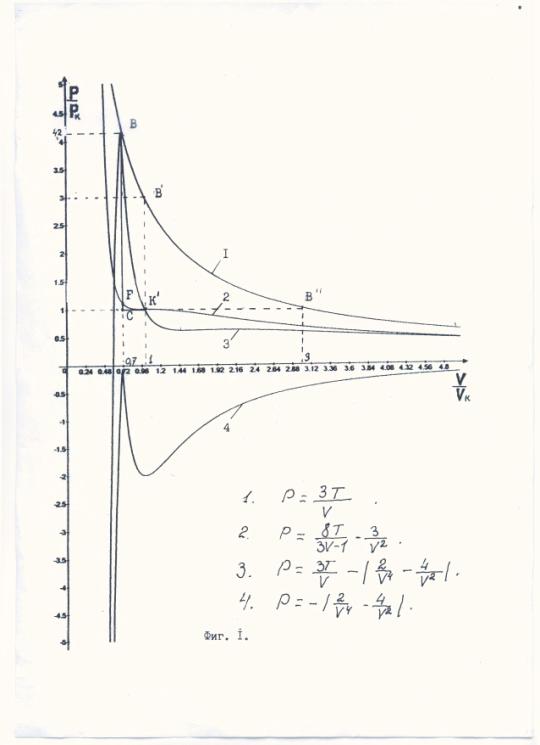
ядро атома. Уравнение (3) фиг.1 предсказывает, что кинетическая энергия атомов
в критической точке в два раза меньше
энергии электронов. Фактор сжимаемости
в критической точке, 
тогда как для
идеального газа этот фактор равен единице.
Таким
образом, в критическом состоянии существует две температуры, одна из которых
обусловлена движением электронов, другая – движением ядер атомов. Электронная
температура не создает давление, но может раскачать атомы измерительного
элемента термометра до температуры внутренней поверхности колбы. В этом случае
термометр отметить не температуру ядер, а температуру термостата.
Вторая
температуру возникает в результате движения ядер. Эту температуру термометр не
«чувствует» поскольку она в три раза ниже электронной температуры. Однако
температура ядер создает давление. Поэтому вторую температуру можно вычислить
по величине произведения (PV) используя уравнения
идеального газа.
Описание
системы с двумя температурами позволяет не только определить критические
параметры, но и придать ясный физический смысл критическим явлениям.
Предлагается
новый способ определения критических параметров.
Для
описания способа представлены два рисунка фиг.1 и фиг.2 . Последовательность
определения критических параметров следующая. На фиг.1 изображены кривые
уравнений, аналитическое выражение которых представлены на этом же рисунке.
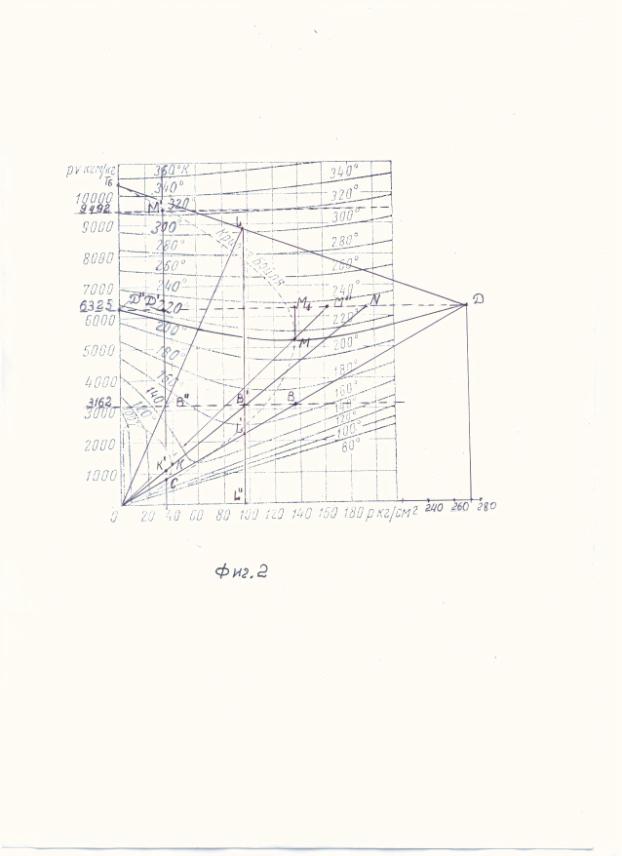
Рисунок на фиг.2 представляет собой PV, P-диаграмму воздуха [5]. По PV, P-диаграмме
определяют точку D.Эту точку пересекают две изотермы с одинаковой
температурой. Одна из этих изотерм 
является
изотермой идеального газа. Вторая изотерма 
, проходящая через максимум кривой Бойля (точка M),
является изотермой реального газа. Давление в точке D - 
(определяется графически).
Изохора DO проходящая через начало координат состоит из двух
равных отрезков DB и BO. На фиг.1 отрезок BC является
частью изохоры DO. Изотерма идеального газа 
на обеих
фигурах имеет одинаковое обозначение. Из фиг.1 видно, что давление в точке B в 4,24
раза выше, чем давление в критической точке 
. Отсюда давление в точке D 
. Поскольку давление
определено, тогда критическое давление равно 
.
Затем
по PV, P – диаграмме определяют 
. Из этого равенства вычисляют обьем в точке D,
который для воздуха равен 
. На фиг.1 видно, что критическая изохора 
равна 
или 
, что совпадает со справочным значением критической
плотности. Поскольку известны 
и 
то, используя
уравнение, 
определяют
критическую температуру. Для воздуха критическая температура 
.
На
фиг.2 отмечены две критические точки K и 
, при этом 
определяется по
новому способу, а точка K определяется по мениску.
Для
сравнения запишем полученные значения критических параметров двумя способами
Из
сравнения следует, что 
и 
практически
совпадают со справочными данными. Однако критическая температура 
, определенная по мениску в 3,68 раз превышает значение
критической температуры 
Далее
определим причины вызывающие расхождение данных при определении критических
параметров двумя способами. По новому способу определение критических параметров
производится путем вычисления по состоянию воздуха далекому от критической точки.
В
новом способе в критической точке не производят измерений.
В
известном способе производятся измерения 
и 
непосредственно
в критическом состоянии.
Таким
образом, в одном способе параметры вычисляются, в другом - измеряются. Забегая вперед, отметим, что
именно эти обстоятельства приводят к возникновению неустранимых противоречий.
По PV, P-диаграмме
определяем, что в точке 
температура 
, в точке 
- 
и в точке 
- 
. Обьем в этих точках соответственно равен 
и 
.
Это
означает, что параметры критической точки должны строго вписываться в сетку
изотерм идеального газа. Точка 
может служить
контрольной точкой, по которой можно судить о точности определения критических
параметров.
Если
согласно этим требованиям подставить в точку 
значение критической
температуры, определенную по способу исчезающего мениска, тогда получим
температуру в точке 
- 
. Данное значение выходит за рамки PV, P-диаграммы
воздуха. Поэтому даже с этой точки зрения критические параметры, определенные
по мениску можно считать ошибочными.
Из
фиг.2 следует, что температура изотермы идеального газа, проходящая через точку
в три раза выше
температуры изотермы проходящей через точку 
. Если непосредственно измерить температуру в точках 
и 
то показания
термометра будет одинаковым, причем термометр будет демонстрировать температуру
. Однако согласно PV, P-диаграмме температура в
точке 
- 
, а точке 
- 
.
При определении
критических параметров по мениску температура измеряется непосредственно в
колбе и в термостате, при этом показания термометра в колбе будет равно
показанию в термостате Ткол.=Ттер.=132,5К. Подставляя результаты измерения в отношение
. Полученный результат является фактором сжимаемости.
По существу фактор сжимаемости ни о чем не говорит,
когда в действительности это выражение является изотермой идеального газа с
температурой, которую можно определить как 
или 
. Здесь 
- показания термометра при исчезновении мениска. Однако
изотерма с температурой 
не является
критической, поскольку она не удовлетворяет требованию контрольной точки 
.
Здесь
важно отметить, что при измерении температуры непосредственно в критической
точке, показания термометра в три раза выше вычисленной температуры по величине
(PV) . Отсюда следует:
1.
Термометры не измеряют действительную температуру в колбе. Показания термометров
отражают температуру термостата, т.е. ту температуру среды, в которую помещена
колба или цилиндр с испытываемым веществом.
2.
Действительную температуру реального газа в любой точке PV, P-диаграммы
можно вычислить по величине (PV).
3. В
каждой точке PV, P-диаграммы можно вычислить
отдельно энергию ядер и энергию электронов.
4.
Теплоемкость одноатомных простых нейтральных молекул зависит только от температуры,
вычисленной по величине (PV).
Особо
следует отметить, что в точках Бойля газовая постоянная не претерпевает каких-либо
изменений. [7]
5. Из
фиг.1 следует, что точка 
является общей
для кривых 
и 
. Это означает, что в точке 
показания термометра
совпадает с действительной температурой реального газа в колбе и температурой
термостата. Существование общей точки указывает на то, что изменение
температуры реального газа должно строго согласоваться с изменением температуры
идеального газа. Это позволяет совместить шкалу 
со шкалой температур
на PV, P-диаграмме.
6. В
критической точке 
действительная
температура реального газа в колбе в три раза ниже температуры термостата, при
этом тепло из термостата не поступает в колбу.
7.
Кривая 
является адиабатой реального газа. При переходе реального
газа из состояния соответствующего точке 
в точку 
тепло из термостата не поступает в цилиндр. В этом
переходе происходит превращение кинетической энергии молекул в потенциальную
энергию электронов.
На
данном процессе можно показать, что при расширении производится работа, но
тепло из термостата не расходуется на выполнение работы. Работу производят
внешние силы, переводя газ из одного состояния в другое. Закон Джоуля применим
в этом случае не только к идеальным, но и к реальным газам.
Отмеченные
особенности реального газа в критическом состоянии обусловлены взаимодействием
электронной оболочки с ядром атома, которое можно описать следующим образом.
Давление
идеального газа возникает в результате столкновения частиц газа с поверхностью
ограничивающей обьем. В реальном газе энергия столкновения передается электронной
оболочке. Критическое состояние газа наступает при такой плотности, при которой
колебание электронов и атомов внутренней поверхности колбы или цилиндра передаются
электронному полю всего газа в колбе, поскольку вес электрона на много меньше веса
ядра, то электронное поле более восприимчиво к внешнему воздействию, чем массивное
поле ядер. Электронное поле строго отслеживает все колебания стенки колбы. В
этом случае температура электронного поля равна температуре термостата. Ядра, в
виду их инертности не могут воспринимать все частоты колебаний электронного
поля, поэтому температура ядер ниже температуры электронного поля и значит ниже
температуры термостата. Возникает система с двумя температурами. Эта система
имеет частично свойство механической колебательной системы и частично свойство термодинамической
системы. В механической колебательной системе перенос энергии осуществляется не
только путем столкновений, но и резонансно-колебательными процессами. Кроме
того, электронное поле по своей природе является колебательной системой. Если в
такое поле поместить термометр, то электронное поле раскачает ядра атомов его
измерительного элемента до такой же температуры, что и температура стенки
колбы, т.е. до температуры термостата. Поэтому показание термометра будут
отражать только температуру термостата.
Электронное
поле не создает давления. Движение ядер создает давление, но его температуру
термометр не «чувствует», поскольку она ниже температуры термостата. Однако
температуру ядер можно вычислить по величине (PV).
Энергия
идеального газа определяется по формуле[6]
Здесь 
. Подставляем это значение в формулу, получим
. (5)
Заменив
в (5) 
и
продифференцировав по температуре, получаем 
.
Отсюда
теплоемкость идеальных газов зависит только от температуры.
Далее
вычислим энергию воздуха в точке 
. Обьем в точке 
- 
. Давление - 
. Энергия в точке 
согласно уравнению (5) равна 
. Теплоемкость в точке
M - 
, здесь R – газовая постоянная воздуха.
Температура
в точке 
равна 
. Однако термометр будет демонстрировать температуру 
. Таким образом, теплоемкость ядер равна теплоемкости
идеального газа, но при этом
температура не измеряется термометром, а вычисляется по величине(
).
Далее
при постоянном объеме переведем газ из точки M в точку 
и вычислим энергию в этой точке. При объеме 
, давление 
, температуре 
энергия 
. Теплоемкость 
.
Разность
энергий 
. Данная энергия равна энергии электронов в точке M.
Далее
из точки M при постоянном давлении переведем газ в точку 
. Энергия в точке 
. Теплоемкость 
.
Таким
образом, энергии в точках 
и 
равны между собой. Не зависимо от процессов в
результате которых газ оказался в точках M, 
и 
его теплоемкость не изменяется.
В процессах
и 
термометр
зафиксирует изменение температуры, только тогда когда температура газа будет
выше 216K, т.е. когда действительная температура увеличится с
180K до 216K. Здесь изменение уровня температуры на 36K
принимается за изобарную 
и изохорную 
теплоемкость.
Здесь теплоемкости 
и 
являются кажущеюся. Если «изобарную» теплоемкость 
измерять слева
и справа от точки M, то эта «теплоемкость» будет убывать. Это означает,
что кажущеюся теплоемкость в точке M является максимальной.
Отсюда следует, что там, где минимум изотермы реального газа на PV,P-диаграмме,
там максимум кажущеюся теплоемкости, и кривая Бойля становится кривой
максимумов 
.
На PV,P-диаграмме
отрезок 
в два раза меньше отрезка 
. Поскольку отрезок 
означает, что
термометр отметит изменение температуры, только когда газ нагреется на 36K, то
отрезок 
показывает, что
в критической точке термометр отметит изменение температуры газа, только когда
газ нагреется с 36K до 108K. Здесь тепловая энергия необходимая для изменения
уровня температуры на 72K принимается за теплоемкость
в критической точке 
.
Описание
причин вызывающих возникновения бесконечной теплоемкости можно выполнить более
подробно, однако основные причины при этом не изменятся.
Далее,
целесообразно привести пример, в котором критические параметры используются при
определении отопительного коэффициента тепловых насосов.
На
фиг.1 изображен термодинамический цикл теплового насоса 
. В качестве рабочего тела в этом цикле используется
реальный газ. На этой же фигуре изображен цикл 
. В этом цикле рабочим телом служит идеальный газ. В
цикле 
работа сжатия 
. Для цикла 
работа сжатия
, что в 6,8раза больше работы сжатия реального газа.
Поэтому отопительный коэффициент теплового насоса работающего на реальном газе 
, а на идеальном газе 
.
Используя
уравнение(5) отопительный коэффициент цикла 
можно выразить
через критические параметры. В этом случае выражение определяющее 
будет иметь
вид:
(6)
Здесь
в числителе теплота, перенесенная за цикл. Знаменатель – затраченная энергия в
процессе переноса тепла.
Выражение
(6) указывает на то, что отопительный коэффициент является следствием закона
сохранения и превращения энергии и закона соответствующих состояний.
Наконец
приведем еще один пример сравнения критических параметров полученных двумя
способами.
Выше
было отмечено, что в каждой точке лежащей на линиях 
и 
показание
термометра соответствует действительной температуре реального газа, при чем в
этих точках реальный газ приобретает свойства идеального газа.
Это
можно показать PV,P-диаграмме. Для
доказательства проведем изохору 
через точку 
. На прямой 
получим точку 
, через которую проведем изобару 
. В точках 
и 
известны
давление и обьем. Используя уравнение (5) вычислим температуру воздуха. Для
точки 
температура 
, а для точки
- 
, что соответствует изотермам воздуха как реального,
так и идеального газа на PV,P-диаграмме.
Возникновение
линии 
предсказывает
уравнение (3) фиг.1. Отрезок 
является частью изохоры 
фиг.2. На этой
линии потенциал Леонардо-Джонса обращается в нуль. Реальный газ преобразуется в
идеальный.
Превращение
реального газа в идеальный на линии 
принимаем
только как результат эксперимента, без физического обоснования.
Таким
образом, на PV,P-диаграмме образуется
треугольник 
. Из этого треугольника следует, что если реальный газ
подвергать сжатию в области от 
до 
, то в газе образуется потенциальная энергия отталкивания.
Возникновение этой энергии обусловлено сопротивлением атомов их бесконечному
сжатию. Если скачкообразно освободить атомы от сжатия, то атомы приобретут
кинетическую энергию. Температура газа увеличится.
Физически,
дросселирование, является процессом, в котором происходит мгновенный сброс
давления, т.е. до перегородки атом находится в сжатом состоянии, после прохождения
перегородки, давление на атом снижается скачком. Уравнение (3) предсказывает
этот процесс.
Если
сжатие и расширение производить в области изменения объема от 
до 
, то процесс дросселирования будет сопровождаться охлаждением.
Отсюда
следует вывод: PV,P-диаграмма позволяет
определить положительный, отрицательный и равный нулю эффект Джоуля-Томпсона,
при чем внутри треугольника 
будет
наблюдаться положительный эффект, вне треугольника – отрицательный. На сторонах
и 
эффект меняет знак, т.е. реальный газ становиться
идеальным газом, а эффект Джоуля-Томпсона равен нулю.
Если
выразить координаты точки 
через
критические параметры воздуха определенные по PV,P-диаграмме, то получаем:
; 
; 
.
Если
координаты этой же точки выразить через критические параметры, полученные с
использованием мениска, то получим:
; 
; 
.
Сравнение
координат одной и той же точки показывает, что в последнем случае определить
положение точки 
на PV,P-диаграмме
невозможно в принципе. Это еще раз доказывает ошибочность определения
критических параметров с использованием мениска.
Следует
добавить, что экспериментально определенные координаты точки 
совпадают с
координатами выражения через параметры 
.[7]
Если
сравнить кривую инверсии на PT-плоскости с треугольником 
на PV,P-диаграмме
воздуха, то нетрудно отметить их сходство. Ясно, что точка 
является точкой
максимума кривой инверсии. Для вандервоальского газа координаты точки инверсии
известны:
; 
; 
.
Для
точки 
координаты
воздуха:
; 
; 
.
Для
воздуха координата точки 
лежит на
изохоре 
. На этой изохоре потенциал Леннарда-Джонсона обращается
в нуль. Реальный газ преобразуется в идеальный газ. Здесь возникновение точки 
обусловлено физическими
свойствами атомов.
Максимум
кривой инверсии вандервоальского газа лежит на критической изохоре NO.
Однако, согласно фиг.1, дросселирование газа слева и справа от этой изохоры
должно приводить к охлаждению газа. Поэтому критическая изобара 
должна
находиться внутри треугольника 
, что и согласуется с PV,P-диаграммой.
Следовательно,
точка максимума кривой инверсии, физически не может лежать на критической
изохоре.
Приведенные
примеры показывают, что критические параметры, определенные по новому способу,
не только устраняют противоречия. Они объединяют незначительные и
фундаментальные закономерности, наблюдаемые в различных процессах реального
газа, и создают неразрывную совокупность теории и эксперимента, которая не
допускает возникновения ошибок.
PV, P – диаграмма
отражает эту совокупность. В каждой точке на PV, P – диаграмме можно вычислить
энергию ядер и электронов. Более того, в каждой точке можно указать причины,
вследствие которых реальный газ приобретает те или иные свойства. Образование
линии 
вызвано тем,
что силы отталкивания равны силам притяжения. Эти силы зависят только от расстояния
между молекулами. Однако, если бы энергия взаимодействия зависела только от
плотности газа, то следовало бы ожидать, что минимумы изотерм должны находится
на критической изохоре при любой температуре. В действительности смещение
минимумов изотерм при низкой температуре происходит вправо, а с повышением
температуры минимум смещается влево от критической изохоры.
По
линии 
обьем от точки 
до точки
пересечения с критической изобарой изменяется в девять раз, а температура по
оси PV изменяется всего в 1,5раза. И те не менее линия 
отражает
зависимость от температуры, а не зависимость от объема. Каждая изотерма
реального газа – дуга, которая стягивается хордой – изотермой идеального газа.
В точках пересечения дуги с хордой реальный газ преобразуется в идеальный. Понятно,
что реальный газ преобразуется в идеальный на оси PV. Однако не ясно, почему
реальный газ приобретает свойства идеального газа при пересечении линии 
. Кроме того, видно, что точки минимума изотерм лежат
на кривой Бойля, а сама кривая Бойля простирается до пересечения с осью PV, где
нет взаимодействия молекул. Другими словами кривая Бойля образуется там, где ее
по определению не должно быть. Значит, возникновение кривой Бойля обусловлено
изменением температуры и не зависит от объема.
Увеличение
температуры также как и увеличение объема
обращает в нуль второй член в скобках модуля уравнения (3).
Повышение
температуры газа не зависимо от объема
делает молекулу нейтральной.
Если
вспомнить о тепловом излучении, то следует отметить, что в замкнутом объеме
давление создается не только тепловым движением молекул, но и тепловым излучением.
Давление фотонов теплового излучения не зависит от объема полости и определяется
только температурой. Под действием давления теплового излучения электронная оболочка
атома становиться сферически симметричной и атом становится нейтральным. При
температуре Бойля световое давление достигает такого значения, при котором
полностью исключается поляризация атома, при этом реальный газ становится идеальным
газом. Ниже температуры Бойля возможна частичная поляризация атома. Эта
поляризация вызывает отклонение изотермы реального газа от изотермы идеального
газа.
Точки максимального
отклонения лежат на кривой Бойля. По мере удаления от этой точки вправо по
изотерме будет накапливаться потенциальная энергия отталкивания. В точках
пересечения изотерм с линией 
энергии притяжения и отталкивания становятся равными, а
фактор сжимаемости равен единице.
Таким
образом, возникновение кривой Бойля обусловлено давлением теплового излучения
на атом, которое делает его нейтральным.
К такому
заключению приводит вид кривой Бойля и область ее существования.
С
точки зрения светового давления следует рассматривать и критическую опалесценцию.
Здесь вытянутость индикатрисы рассеяния в сторону падающего светового потока
обусловлена тем, что световой поток, продавливая газ, образует конус, который и
формирует индикатрису рассеяния. При этом, чем меньше длина волны, тем меньше
площадь основания конуса и тем больше его высота. Отсюда вытянутость
индикатрисы рассеяния обратно пропорциональна площади основания конуса.
Далее,
в качестве заключения, рассмотрим возникновение бесконечной сжимаемости в
критической точке.
Из
фиг. 1 видно, что в критической точке потенциальная энергия достигает максимального
значения, которая при этом в два раза больше кинетической энергии. Это означает,
что ни в какой другой точке подобного соотношения энергий быть не может. Это
единственная точка, параметры которой кратны параметрам замечательных точек на PV, P – диаграмме.
Ось PV равнозначна оси температуры. Из фиг.2 следует, что температура в точке
в три раза ниже
температуры в точке 
. Однако при измерении температуры от 
до 
показание термометра будет постоянным. Термометр будет
демонстрировать постоянную температуру равную 
. Этот эффект описан выше. Современная трактовка этого
же эффекта заключается в том, что при постоянном давлении и постоянной температуре, когда изобара совпадает с
изотермой, теплоемкость 
в критической
точке равна бесконечности. Это означает, что при подведении неограниченного
тепла к газу в критической точке, его температура не изменяется. Однако это обоснование
противоречит закону сохранения и превращения энергии. В действительности в
каждой точке на отрезке изобары 
можно вычислить
температуру по величине PV, используя уравнение идеального
газа.
Причем
при 
уравнение
преобразуется в уравнение Гей-Люссака 
.
Отсюда
следует, что 
выполнить
физически невозможно, поскольку при изменении объема происходит изменение
температуры, причем это изменение происходит в результате превращения
потенциальной энергии взаимодействия в кинетическую энергию, т.е. без подвода
тепла и постоянной температуры термостата.
Здесь
важно также отметить, что подобное изменение температуры газа может происходить
только при условии, когда эта температура ниже температуры термостата. Данное
обстоятельство указывает на то, что два тела, находясь в тепловом контакте, при
различной температуре могут не обмениваться тепловой энергий. Этот факт требует
уточнения самого определения температуры и способа ее измерения.
CRITICAL PARAMETERS AND CRITICAL PHENOMENA
Konov A.
F.
In
article is shown that determination of critical parameters on the moment of disappearance
of a meniscus leads to emergence of the unsoluble problems caused by that in a
critical point the thermometer takes not gas temperature in a flask, and
thermostat temperature. In a critical point the temperature of the thermostat
is three times higher, than gas temperature in a flask. The description of a
way of determination of critical parameters with use of PV, the P-chart is
provided. Comparison of the critical parameters received in two ways, shows for
example, as in a critical condition it кажущеюся to a thermal capacity. Here
the thermal energy necessary for increase in level of temperature in 2 times
exceeding critical temperature of gas, wrongly take for energy necessary for
heating of real gas on 1K. Coordination of the critical parameters determined
by a new way, with physical properties of the gas, observed in various
processes, creates set of the theory and experiment which doesn't allow emergence
of mistakes.
Key words: thermal radiation, length of a wave, a maximum of a range of radiation,
Planck's formula, the law of shift of Wine, pressure of radiation in the closed
cavity.
Литература
1. Конов А.Ф.
Обоснование принципа работы теплового насоса с максимальным отопительным коэффициентом. //Альтернативная
энергетика и экология. №1. 2011г.
2. Конов А.Ф. Об
ошибке в теории теплового излучения //Математическая морфология. Электронный математический и медико-биологический
журнал. – Т.10. – Вып.4 – 2011.
3. Кикоин И.К.,
Кикоин А. Молекулярная физика. – М. Физматизд, 1963 С.233-235.
4. 4. Сб.ст.
Уравнение состояния газов и жидкостей. К 100-летию уравнения Ван-дер-Ваальса. Отв. Ред. Член-корр. АН
СССР И.И.Новиков. – М.: «Наука» 1975г.,
с.173
5. Энциклопедический
справочник. Т.1 / Гл. редактор Кобулошвили Щ.Н. – М.: Госторгиздат, 1960г., с.427-488.
6. Ландау Л.Д.,
Лифшиц Е.М. Статистическая физика. – М.: «Наука» 1976г., с.185.
7. Физическая
энциклопедия. Т.1 / Гл. ред. Прохоров А.М. – М.: «Советская энциклопедия» 1990г.
ГУ Всероссийский научно-исследовательский институт
сельскохозяйственной метеорологии
(ГУ ВНИИСХМ)
г. Обнинск
Поступила в
редакцию 10.09.2012