Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 11. -

Вып. 3. - 2012. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-35-html/TITL-35.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-35-html/cont.htm

УДК 661

Анализ техники оценки корреляционного интеграла диаграмм ритма сердца

Ó 2012 г. Плеханов А.А.

(plekhanov.doc)

В статье рассматриваются методические аспекты при расчете корреляционного интеграла при анализе диаграмм ритма сердца: применение технологии корреляционного анализа к хаосграммам реальных диаграмм ритма сердца, назначение величины задержки tau; выбор размерности пространства вложения М; определение величины ребра кубика-ловушки . Получены оригинальные оценочные закономерности, позволяющие адекватно определять вышеуказанные параметры.

Ключевые слова: корреляционный интеграл, ритм сердца.

В известной технике расчета фрактальной размерности () фазовых портретов динамических систем центральное место занимает корреляционный интеграл (), показывающий плотность скопления точек фазового портрета относительно выбранного состояния [1]. Сам алгоритм расчета фрактальной размерности (ФР) считается отлаженным для известных моделей динамических систем, таких как аттрактор Лоренца или Хеннона. Для реализаций реальных сигналов ритма сердца (ДРС) в формах хаосграмм (ХГ) существует неопределенность в самой возможности применения к ним технологии расчета ФР и интерпретации результатов анализа. С методической точки зрения, при расчете существует ряд подлежащих обсуждению моментов, связанных с выбором значимых параметров: размерность пространства вложения M; величина задержки компонентов исходного вектора , отражающего регистрируемый процесс; величина стороны ребра кубиков , которыми покрывается исследуемый фазовый портрет. Приведем формулу расчета для более ясного взгляда на проблему:

(1)

В формуле 1 функция Хэвисайда используется для определения принадлежности точки фазового портрета текущему кубику, покрывающему часть аттрактора. Выражение , по известной методике [1], для M = 4 переписывается в виде:

(2)

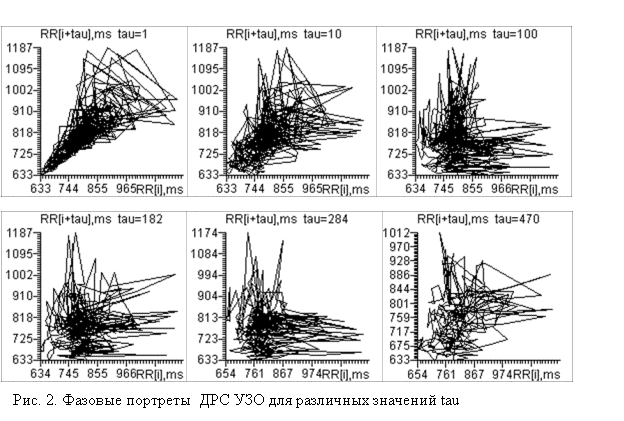
Формула 2 показывает переход от одномерного вектора к M-мерному вектору, описывающему ХГ в М-мерном пространстве. В каждом из векторов M-мерного аттрактора используется задержка , которая выполняет роль фильтра высоких частот. Это легко доказывается при наблюдении трансформации топологической структуры 2D ХГ при изменении (рис. 2).

На рис. 2 показано видоизменение ХГ ДРС условно здорового организма (УЗО). ХГ на рис. 2 (tau=1) имеет выделенную область значений (аттрактор) в форме веретена, а также набор простых геометрических фигур большой площади, наличие которых обусловлено присутствием на исходной RR-интервалограмме (рис. 1) высокоамплитудных значений – брадипауз.

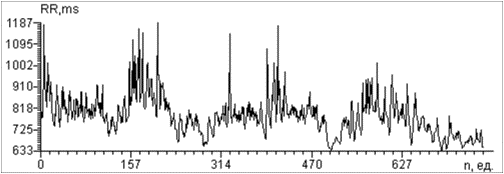
Рис. 1. ДРС УЗО

Простые геометрические фигуры предлагается трактовать наложенными друг на друга с небольшим смещением. Смещение обусловлено отклонениями в значениях амплитуд бради пауз. Практика показывает, что даже при относительно невысоких значениях tau (рис.2, tau=10) аттрактор ХГ трансформируется в клубок; простые геометрические фигуры также изменяются, но с эффектом поворота направо и налево относительно линии, образованной началом отсчета на текущем графике ХГ и условным центром аттрактора. Последнее является следствием чередования (периодичности) компонент сигнала высокой и низкой амплитуд. Чем ближе подобранное значение tau приближается к периоду определенной компоненты или становится кратным ему (речь именно о компонентах, а не только о гармониках), тем сильнее составляющие компоненты группируются около особой точки на ХГ. Принадлежность полигона гистограмм виртуальной диаграммы ритма сердца (ВДРС) [2] к нормальному распределению объясняет единственный аттрактор на фазовом портрете на разных величинах задержки, что обусловлено абсолютной случайностью каждого значения такого ряда. По всей длине ДРС присутствуют компоненты, порожденные активностью барорецепторов и вагуса, что привносит в ритмограмму множественные повторяющиеся локальные тренды, со сложной внутренней структурой. По рис. 2 (tau=100) видно, что аттрактор трансформируется в «неправильный крест», на котором каждая ветка, уходящая от аттрактора, является плотным скоплением точек в фазовом пространстве, и также имеет место за счет периодических включений определенных компонент сигнала, но на более длительном интервале регистрации. Пользуясь фильтрующим информацию свойством tau возможно получить информацию о фазовых траекториях любых компонентов сигнала, вплоть до трендовых (рис. 2, .

Несмотря на качественное различие структурных форм ХГ для разных величин задержки, значения корреляционного интеграла быстро стабилизируются и в последующем имеют малые отклонения от среднего. Тем не менее, наблюдается отличительная закономерность динамики в зависимости от tau. Суть её в том, что при определенном наблюдается высокая инвариантность корреляционного интеграла по отношению к tau. При этом выполняется требование, изложенное в [3]: «Величина должна стремиться к нулю, но не должна быть слишком малой». Эта, довольно свободная формулировка, являющаяся рекомендацией по назначению, по мнению автора, может быть перефразирована в виде: «Величина должна учитывать информацию о ширине амплитудных уровней на ДРС». Последняя формулировка вытекает из экспериментальных графиков зависимости (рис. 4), построенных для ДРС УЗО, насыщенной составляющими различного сорта: нормальный ритм в покое; ортостатическая проба; проба с фиксированным темпом дыхания (рис. 3).

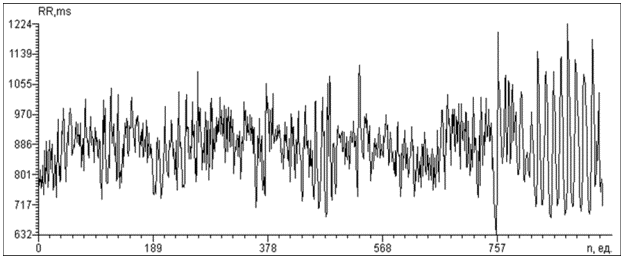
Рис. 3 ДРС УЗО, насыщенная различными видами составляющих

На рис. 4 представлено семейство графиков зависимости для различных . Из семейства графиков видно, что на относительно малых значениях стороны ребра кубиков величина корреляционного интеграла убывает с возрастанием tau, а после некоторого значения начинает возрастать. Величина , при которой зависимость приобретает свойство инвариантности находится, для данной RR-интервалограммы (рис. 3), около значения в 220 ms, которое как раз захватывает область аттрактора на фазовых портретах. Таким образом, специально подобранное значение может стать универсальным инструментом в определении площади, занимаемой аттрактором на фазовой плоскости ХГ.

Рис. 4 Семейство графиков зависимости для различных и

для постоянного М

Если в качестве меры инвариантности зависимости взять среднеквадратичное отклонение каждой функции семейства и представить относительно , получится гладкого вида функция, состоящая из одного локального максимума и, следующего за ним, локального минимума, в последствии являющаяся константой (рис. 5).

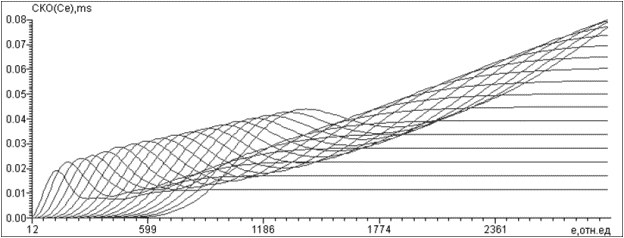Рис. 5 Семейство функций для разных значений М.

Первые локальные максимумы функций (рис. 5), по мнению автора, обусловлены тем, что кубик, с ребром по большей части посещает наиболее плотные скопления фазовых состояний, содержащих минимальное количество пустот, а, следовательно, при неизменной топологической структуре ХГ, оптимально покрывает фигуру (или тело, если речь идёт о размерности М > 2). Высокая вариативность функции отражает высокую чувствительность корреляционного интеграла к изменению топологии ХГ с возрастанием величины задержки tau. В этом случае более прозрачным становится требование к оптимальному покрытию ХГ кубиками с ребром. Также обращает на себя внимание тот факт, что при изменении размерности пространства вложения М амплитуда локальных максимумов функции возрастает по закону, близкому к линейному.

Последующий локальный минимум функций трактуется как возрастание количества пустот на фазовом портрете, захватываемых ловушкой при возрастании и повышение инвариантности функции .

а

б

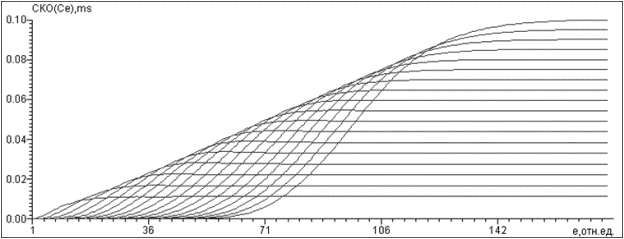
в

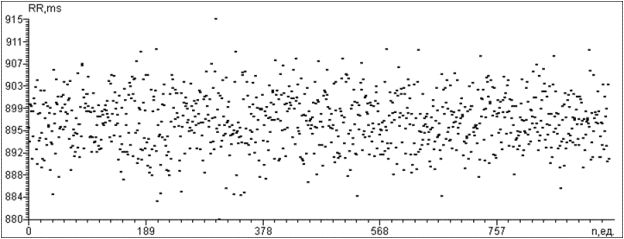
Рис. 6. Графики: а) ВДРС, б) Семейство функций для ВДРС, в) Семейство функций для разных значений М для ВДРС

Константные значения функции (рис. 5) объясняются тем, что величина начинает стремиться к бесконечности и все значения ХГ оказываются захваченными одной ловушкой. При этом условие о должных величинах перестаёт выполняться.

Сложность структуры функции вероятнее всего является продуктом степени разнообразия топологических структур ХГ. Это становится очевидным при рассмотрении ВДРС(рис. 6, а) [2], сгенерированной по нормальному закону для исследуемой ДРС УЗО (рис. 3). На рис. 6, в представлено семейство функций для ВДРС в виде набора s-образных кривых, монотонно возрастающих с увеличением . S-образность, свойственная функциям, показывающим насыщение параметра, и в данном случае отражает стабильную систему градиента точек фазового портрета для ВДРС. Стабильность структуры, в данном случае, подтверждается самой методикой генерации ВДРС.

Функции имеют общую топологию лишь для одной структуры фазового портрета, например для всех ВДРС, т.к. последним присуще наличие единственного аттрактора, который сгенерирован по одному и тому же закону. В случае отклонений в законе распределения исходной ДРС от одномодального в структуре фазового портрета начинают появляться пустоты сильно влияющие на оценку корреляционного интеграла. Примером такой ДРС может служить ритмограмма на рис. 7, а.

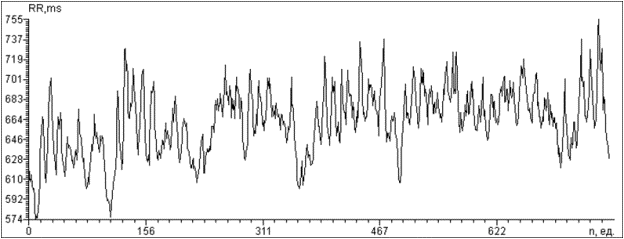
а

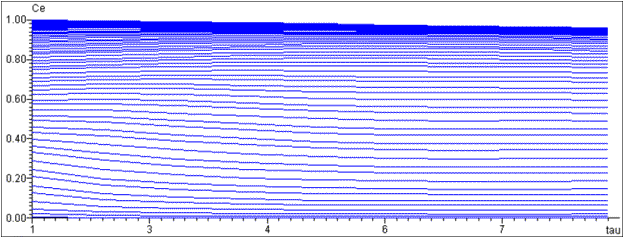
б

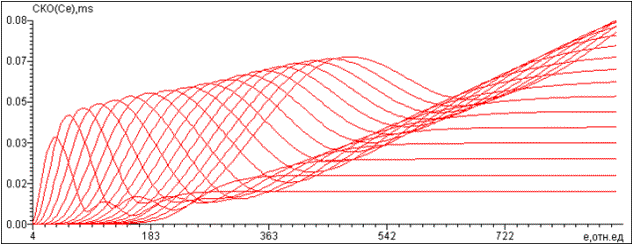
Рис. 7 Графики: а) ВДРС, б) Семейство функций для ВДРС, в)Семейство функций для разных значений М для ВДРС

На рис. 7, в показано семейство функций для ДРС на рис. 7, а. Особенностью некоторых функций (для малых значений М), входящей в набор семейства является наличие двух локальных максимумов и двух локальных минимумов. По мнению автора это объясняется неоднородностью в структуре ХГ ДРС, а именно: после оптимального покрытия ХГ на фазовой плоскости кубиками-ловушками, дальнейшее увеличение , как уже говорилось, приведет к захвату пустых областей, снижающих величину корреляционного интеграла; при относительно стабильной структуре ХГ, в последующем, функция должна принять константное значение, но тем не менее за счет дальнейшего увеличения и при потере значимости объёмов пустых мест на ХГ функция снова возрастает. В таком случае, на малых величинах М возникает неадекватность рассчитанного значения , связанная скорее с методической неопределенностью при покрытии ХГ кубиками-ловушками. Методически, ситуация исправляется выбором большего значения М и форма функции становится подобной форме функции на рис. 5. Для ВДРС на рис. 7, а семейство функций выглядит идентично семейству на рис. 6, в. (рис. 8).

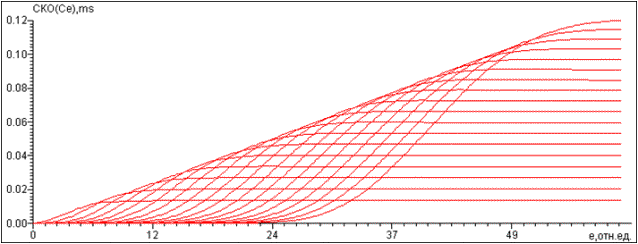
Рис. 8 Семейство графиков зависимости для различных М

Высокая степень подобия s-образных функций для ВДРС и методический подбор величины пространства вложения М для реальных ДРС может представлять собой критерий однородности аттракторов ХГ ДРС. Таким образом, величина приобретает триггерную зависимость от формы функции, где критерием выбора первой служит соответствие топологии функции её форме на рис. 5.

Выводы

1. В применении технологии фрактального анализа к ХГ ДРС получено свойство инвариантности корреляционного интеграла к величине задержки, при определенных , объясняемое попаданием в кубик-ловушку аттрактора ХГ; установлена нелинейная связь между чувствительностью корреляционного интеграла, к топологии ХГ и величиной .

2. Получен критерий оптимального покрытия топологии ХГ кубиками-ловушками как величина , приходящаяся на первый локальный максимум функции .

3. При увеличении размерности пространства вложения М амплитуда локальных максимумов функции возрастает по закону, близкому к линейному, что соответственно указывает на линейное усложнение топологии ХГ; для ХГ с большой неоднородностью макроструктуры, на малых значениях М, возникает неадекватность определения величины корреляционного интеграла, корректируемая повышением размерности пространства вложения.

4. В качестве величины tau предлагается брать единичную задержку, т.к. достаточный вклад при трансформации ХГ вносит величина размерности пространства вложения М.

5. Выбор величины размерности пространства вложения предлагается брать в случае обнаружения первой функции семейства с единичными локальными минимумом и максимумом. В качестве должного значениястороны ребра кубика-ловушки предлагается брать , приходящуюся на первый локальный максимум функции .

ЛИТЕРАТУРА

1. Кузнецов А.А., Плеханов А.А. О технике оценки фрактальной размерности фазовых портретов динамических систем. // Физика и радиоэлектроника в медицине и экологии. VIII международная научно-техническая конференция. Доклады в 2-х книгах. Кн. 1. ВлГУ, Владимир. 2008. С. 152-156. – ISBN 978-5-93767-039-7

2. Кузнецов А.А. Энтропия ритма сердца: монография. – Владимир: Изд-во Владим. гос. ун-та, 2009. – 172 с.

3. Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания. – М.: Наука. 1987. – 424 с.

Analysis of technology assessment of the correlation integral RR-intervalogramm

Plekhanov A. A.

The article discusses methodological aspects of the calculation of the correlation integral in the analysis of RR-intervalogramm: the appointment of the delay tau; choice of embedding space of dimension M, the determination of the edges of the cube trap ε. We obtain estimates of the original laws that allow adequate to define the above parameters.

Key words: correlation integral, analysis of RR-intervalogramm.

Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых» (ВлГУ).

Кафедра «Биомедицинской инженерии».

Поступила в редакцию 1.09.2012.