Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 12. -

Вып. 1. - 2013. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/TITL-37.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/cont.htm

УДК 623.465

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СИСТЕМЫ НАВЕДЕНИЯ С ОПТИМАЛЬНЫМ УПРАВЛЕНИЕМ

Ó 2013 г. Финогенов С. Н., Хамра В. Або

(finogenov.doc)

В данной работе изложен способ формализации математических моделей систем наведения с оптимальным управлением. В результате предложена обобщенная структура формализованной математической модели системы наведения.

Ключевые слова: математическая модель систем наведения.

Задача формирования оптимальных управлений является в общем случае нелинейной задачей оптимального управления с ограничениями на управляющие и фазовые переменные. Оптимизация проводится с помощью формализованной математической модели (ФММ) процесса наведения, называемой обычно контуром наведения. ФММ должна включать: систему дифференциальных уравнений кинематики и динамики движения ракеты; уравнения измерений; области определения правых частей уравнений; интервал измерения времени; класс допустимых управлений; законы распределения и числовые характеристики возмущений.

При синтезе оптимальных управлений и реализации их в СУП используются два типа ФММ:

использование уравнений в форме Коши;

векторный вид уравнений наведения.

Первый тип моделей используется при постановке задач; второй – при поиске конкретных решений.

Модель ракеты с использованием уравнений в форме Коши можно представить в виде

где	t	–	время, определенное на интервале [ti, tf];
	хр	–	вектор фазовых координат;
	εр	–	n-мерный вектор возмущений;
	Ggi	–	параметры, определяющие динамику ракеты;
	Gкi	–	параметры кинематических связей;
	ggi	–	m-мерный вектор случайных отклонений параметров ракеты;
	ауi	–	параметры, определяющие функционирование системы управления и стабилизации;
	Тм	–	метеорологические факторы (плотность, давление, температура воздуха и т. д.);

u = {u₁, u₂}, u₁ – вектор управлений с обратной связью (законы управления рулями), u₂ – вектор управлений без обратной связи (управляющие функции, алгоритмы).

Множества фазовых координат G_x и их производных считаются заданными: x_р(t) Î , Î. Заданные множества , определяются функциональными структурами, конструктивными особенностями ракеты.

Области определения х_р, u, f характеризуются неравенством вида > 0 и т. д.

Вектор измерений у_р(t) удобно представить в виде

Y_р(t) = Ψ_р(t, x_р, u, g_и), (1)

где g_и – вектор случайных инструментальных ошибок измерения.

Компонентами вектора измерений y(t) являются значения проекций линейных и угловых скоростей, линейных ускорений на оси чувствительности датчиков линейных ускорений (ДЛУ) и угловых скоростей, а также углы, характеризующие взаимное положение осей ракеты относительно базовой системы координат.

Вектор вычисленных элементов движения у_рв(t) можно записать в виде

y_рв(t) = Ψ_рв(t, x_р, u, g_и, g_м),

где g_м – вектор методических ошибок вычисления.

С учетом выражения (1) можно записать так:

y_рв(t) = F_в(y(t)). (2)

Возможны два случая:

количество выходных координат x_р(t) совпадает с количеством измеренных параметров y_р(t);

число скалярных составляющих x_р(t) больше количества измеренных параметров y_р(t).

Второй случай является более общим: при синтезе управлений решается задача в условиях недостаточной информации. Если представить, что параметры характеризуются к-мерным вектором

Y_р(t) = {y₁(t), …, y_к(t)},

то связь между x_р(t) и y_р(t) можно представить через некоторый непрерывный оператор R_р, называемый кинематическим:

y_р(t) = R[x_р(t), t].

Законы распределения и числовые характеристики вектора инструментальных и методических погрешностей, как правило, задаются в составе исходных данных.

На рисунке 1 представлена структурная схема ФММ управляемого объекта.

Модель кинематики движения ракеты и цели (относительного движения):

= f(t, х_к, u₂, ε_к),

где х_к – вектор фазовых кинематических координат

ε_к – n-мерный вектор фазовых возмущений (движение цели, помехи и т. п.).

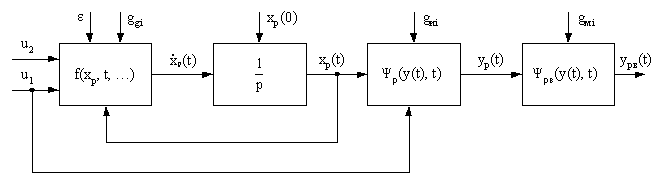
Рисунок 1 – Структура ФММ управляемого объекта

Множество фазовых координат G_хк и их производные считаются заданными х_к(t) Î G_хк; Î .

Вектор измерений у_к(t) можно представить в виде

у_к(t) = Ψ(t, x_к, u₂, g_ки),

где g_ки – вектор случайных инструментальных ошибок измерений (оценок).

Компонентами вектора измерений у_к(t) могут являться значения абсолютных координат и параметров движения цели и ракеты; координат и параметров относительного движения «ракета – цель», проекций линейных ускорений на оси чувствительности ДЛУ.

Вектор вычисленных элементов кинематики движения у_кв(t) можно записать в виде

y_кв(t) = Ψ_к(t, x_к, u₂, g_ки, g_км),

где g_км – вектор методических ошибок вычисления (оценок).

ФММ кинематики движения представлена на рисунке 2.

Рисунок 2 – Структура ФММ кинематики движения

Модель системы управления полетом определяется алгоритмами программно-терминальных управлений (ПТУ), в частности:

алгоритмами ПТУ на основе функциональных зависимостей;

алгоритмами оптимального терминального управления;

аппроксимирующими функциональными зависимостями квазиоптимального терминального управления.

Задача оптимизации для динамической системы, описываемой векторным дифференциальным уравнением в форме Коши,

t Î [t₀, t_f],

где x(t) = {x₁(t), …, x_n(t)}^Т – вектор-функция управляющих параметров заключается в определении управления , минимизирующее значение функционала F₀

При этом должно быть выполнено условие Î U при всех t Î [t₀, t_f], где U – ограниченная замкнутая область m-мерного пространства E_m и дополнительные ограничения

i =1, 2, …, q. (3)

Здесь – функционалы; обозначение – функция, взятая целиком, как элемент функционального пространства, т. е. – вектор, являющийся значением в момент времени t.

Функционалы (3) можно интерпретировать как некоторые терминальные фазовые ограничения

i =1, 2, …, q. (4)

Одно из ограничений вида (4) можно сформулировать как условие, чтобы фазовая траектория принадлежала некоторой заданной области S фазового пространства:

Î S при всех t Î [t₀, t_f].

Вопрос о выборе критерия оптимизации решается в зависимости от дополнительных требований, например, как минимум перегрузок, затрат на управление, максимального быстродействия и др. В общем случае функционал (3) удобно записать в виде

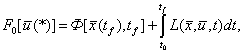
где описывает влияние на критерий значений фазовых координат в конечный момент времени t_f; функция характеризует зависимость критерия оптимизации от изменения фазовых координат и от управления в процессе полета ракеты.

Условие Î U при всех t Î [t₀, t_f] на практике обычно имеет вид

где и – нижняя и верхняя границы допустимых значений управляющих параметров.

Одним из путей решения задачи оптимизации с учетом ограничений вида (3) и (4) является использование метода штрафных функций, который считается простейшим из числа существующих методов (принцип максимума Л. С. Понтрягина, динамическое программирование и др.) [1].

Суть его состоит в следующем.

Если на интервале t Î [t₀, t_f] задано ограничение в виде неравенства , то критерий оптимизации F₀ может быть преобразован путем введения дополнительного слагаемого к виду

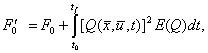
где

Очевидно, что возможны и другие варианты задания формы функции штрафа. Единственным требованием к ним является то, чтобы они равнялись нулю или были бы малы внутри и на границе допустимой области и положительны и велики за границей этой области. В общем случае, если ограничения на управляющие и фазовые переменные имеют вид и , то можно записать критерий оптимизации в виде

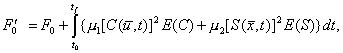(5)

где μ₁, μ₂ – постоянные коэффициенты.

Аналогично можно ввести штрафные функции за несоблюдение терминальных фазовых ограничений:

Соответствующие преобразования критерия оптимизации можно рассматривать как введение дополнительного специального «штрафа» за невыполнение заданных ограничений. Метод штрафных функций, таким образом, позволяет сводить задачу с ограничениями к задаче на безусловный экстремум – классической вариационной задаче Лагранжа [1]. Оптимальное управление для такой задачи определяется решением двухточечной краевой задачи. Подбором постоянных коэффициентов μ_i ограничения могут быть приближенно удовлетворены. Чем больше выбранные значения μ_i, тем меньше будет соответствующее значение интеграла в расширенном критерии (5). Однако, если μ_i брать слишком большим, то итерационные алгоритмы будут в основном стремиться удовлетворить соответствующее ограничение, а не минимизировать исходный критерий F₀. В результате сходимость к удовлетворительному решению будет весьма медленной.

Задача оптимизации управления в системах терминального наведения ракет решается с использованием достаточно сложных математических моделей. Существенное упрощение решения задачи дает переход от точной задачи к так называемой модельной [1]. Построение оптимального управления для модельной задачи рассматривается как квазиоптимальное для точной задачи, а управляющие параметры, полученные с таким управлением, в качестве квазиоптимальных.

В результате решения модельной задачи оптимизации устанавливается структура закона управления и функциональные зависимости компонентов фазового состояния, используемых при формировании алгоритмов управления. Функциональные зависимости устанавливаются при помощи аппроксимации изменения во времени компонентов фазового состояния.

Одним из методов решения модельной задачи оптимизации можно считать аналитическое конструирование [1].

С учетом вышеизложенного формализованную математическую модель системы наведения можно представить обобщенной структурой вида (рисунок 3)

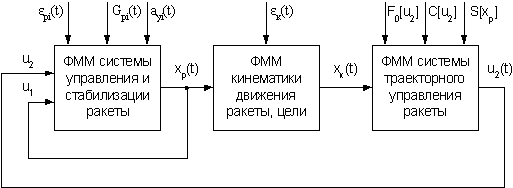
Рисунок 3 – Обобщенная структура ФММ системы наведения

На рис. 3 F₀[u₂] – функционал оптимизации траекторного управления полетом ЗУР, С[u₂], S[x_p] – области ограничений на управляющие и фазовые переменные.

Литература

1. Красовский А. А., Буков В. Н., Шендрик В. С. Универсальные алгоритмы оптимального управления непрерывными процессами. М., Наука, 1977. 271 с.

MATHEMATICAL MODEL OF SYSTEM OF TARGETING WITH OPTIMUM CONTROL

Finogenov S. N., Hamra V. Abo

In this work the way of formalization of mathematical models of systems of targeting with optimum control is stated. The generalized structure of the formalized mathematical model of system of targeting is as a result offered.

Key words: mathematical models of systems of targeting.

Военная академия войсковой ПВО

Вооруженных Сил Российской Федерации

 имени Маршала Советского Союза А.М. Василевского

(ВА ВПВО ВС РФ)

Поступила в редакцию 3.02.2013