Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 12. -

Вып. 1. - 2013. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/TITL-37.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/cont.htm

 

УДК 621.391.161

 

ИЗМЕРЕНИЕ ДАЛЬНОСТИ ДО ЦЕЛЕЙ С ПЕРЕКРЫВАЮЩИМИСЯ ВО ВРЕМЕНИ СИГНАЛАМИ

 

Ó 2013 г. Илларионов Е. А., Коцур А. А.

 

(illarionov.doc)

 

В данной работе изложен алгоритм разрешения по дальности двух перекрывающихся во времени сигналов с существенно различающимися амплитудами. Принцип действия алгоритмов разрешения эхо-сигналов целей основан на нормировании сигнала к амплитудам источников, его образовавших. Подобное нормирование позволяет исключить зависимость точности измерений от соотношения амплитуд источников сигнала и в значительной степени ослабить эффект маскирования слабого сигнала более мощным. Для оценки возможности использования метода нормирования амплитуд в дальномерной области необходимо получить аналитическое выражение для сжатого ЛЧМ сигнала.

Ключевые слова: метод нормирования амплитуд.

 

1. Модель сжатого ЛЧМ сигнала

 

При воздействии на вход измерителя сигналов М источников переизлучения и выполнении условий линейности распространения сигнала в пространстве и тракте обработки, каждый дискретный отсчет ЛЧМ сигнала с номером s можно представить выражением

 

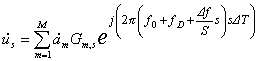,                                      (1)

 

где  – комплексная амплитуда сигнала m-го источника, – функция, принимающая значение 0 или 1 и определяющая относительное запаздывание сигналов различных источников друг относительно друга,  f0 – средняя частота спектра ЛЧМ сигнала, fD – доплеровское приращение частоты, Df – девиация частоты ЛЧМ сигнала, S – количество дискрет, из которых состоит ЛЧМ импульс, DТ – период дискретизации (примем его равным 1/(2 f0)).

Для сжатия необходимо каждую реализацию из S дискретных отсчетов принятого сигнала по принципу «следящего окна» перемножить со своей копией (осуществить корреляционную обработку).

 

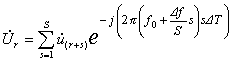r=1…R-S,                       (2 )

где R – количество дискрет, укладывающихся на период повторения.

Рассмотрим односигнальную ситуацию, после чего полученные результаты обобщим на другие случаи. Пусть взаимное положение принятого сигнала и копии такое, как показано на рисунке 1.

 

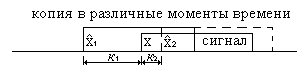
Рисунок 1 – Пример взаимного положения принятого сигнала и копии

 

k– количество дискрет, на которые копия запаздывает по отношению к сигналу (взаимное рассогласование, или разность запаздывания сигнала Х и копии относительно нулевой дальности). С учетом этого подставим в выражение (2) значение выражения (1) и проведем необходимые преобразования. В результате получим

 

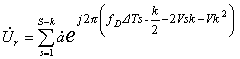,                                     (3)

где .

Выражение (3) представляет собой сумму S-k членов геометрической прогрессии, знаменатель которой можно получить в виде

 

.                                                         (4)

 

С учетом этого выражение (3), раскрытое как сумма S-k членов геометрической прогрессии примет вид

 

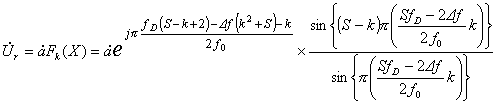.                 (5)

 

Из анализа этого выражения можно сделать следующие выводы:

1.     Огибающая сжатого ЛЧМ сигнала имеет комплексный характер, т.е. в зависимости от рассогласования меняется не только ее амплитуда, но и фаза.

2.     И амплитуда, и фаза мгновенных значений огибающей в высшей степени нелинейно зависят от рассогласования между сигналом и его копией.

 

2. Нормирование сигнала к собственным амплитудам

Для получения алгоритма измерения дальности двух целей необходимо иметь две независимые тройки отсчетов огибающей ЛЧМ сигнала. Эти отсчеты можно получить, используя пару соседних импульсов. Значения напряжений будут выглядеть в виде

 

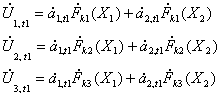                                          (6)

 

для первого импульса и в виде

 

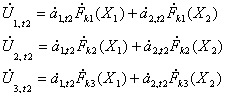                                      (7)

 

для второго импульса. В этих выражениях величины представляют собой значения огибающей сигнала при различных значениях рассогласования. Предполагается, что амплитуды источников за интервал зондирования изменились.

Из полученных, таким образом напряжений составим систему уравнений вида

 

,

 

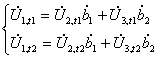которая в матричном виде будет выглядеть

 

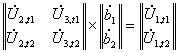.                                      (8)

 

Для отыскания неизвестных коэффициентов  воспользуемся правилом Крамера [2], согласно которому

 

,                                                      (9)

 

где D – определитель системы (8), Dm – определитель, полученный заменой m-го столбца определителя системы столбцом свободных членов.

 

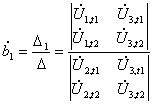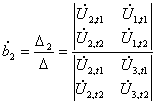,  .                              (10)

 

Если в выражения (10) подставить значения напряжений из (6,7), получим

 

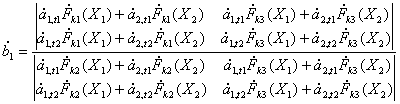.                       (11)

 

Перепишем числитель и знаменатель этого выражения в виде произведения определителей

 

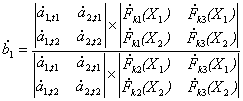.                                          (12)

 

Определители, составленные из амплитуд одинаковы в числителе и знаменателе выражения (12), в результате чего они сокращаются при делении, и выражение для коэффициента принимает вид

 

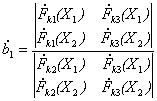.                                                     (13)

 

Аналогично для второго коэффициента получим

 

 

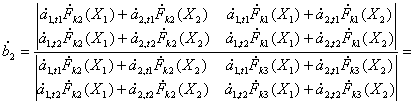
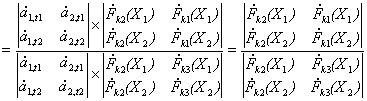.                      (14)

 

В итоге искомые коэффициенты  оказываются независящими от амплитуд источников, образовавших входной сигнал. Величина их определяется только значениями огибающей принятого сигнала, которые в свою очередь однозначно связаны с дальностями источников переизлучения. Именно это позволяет считать процесс нахождения указанных коэффициентов эквивалентным нормированию входного сигнала к амплитудам образовавших его источников, причем указанное нормирование можно осуществлять независимо от соотношений и скорости флуктуаций амплитуд.

Следующим этапом является нахождение неизвестных дальностей источников излучения. Для этой цели необходимо в выражения (13, 14) подставить значения огибающей и выразить из полученных зависимостей дальности до источников излучения.

 

3.     Измерение дальностей до источников переизлучения

 

Если в выражения (13, 14) подставить истинное значение огибающей вида (5), то, как отмечалось выше, получится крайне нелинейная система уравнений, решить которую можно только итерационными методами [3]. В силу известных недостатков такого пути остается заменить истинное значение огибающей ЛЧМ сигнала более простой аппроксимирующей функцией.

В соответствии с исходными данными были рассмотрены следующие варианты:

1. Огибающая сжатого ЛЧМ импульса описывается зависимостью вида , где Хm – времена запаздывания сигналов целей, kХ0 – рассогласование между временем образования пикового значения огибающей и временем, в которое взят отсчет для измерения. Близкую к данной форму огибающая ЛЧМ сигнала будет иметь после весовой обработки, которая производится с целью подавления боковых лепестков.

2. Огибающая сжатого ЛЧМ импульса описывается зависимостью вида

 

,

 

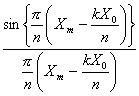где n – количество отсчетов в главном лепестке огибающей сжатого сигнала.

В первом случае выражения для коэффициентов вида (13, 14) будут выглядеть

 

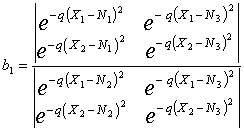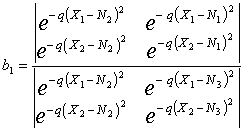,   ,          (15)

 

где Nk =kX0. Если все три отсчета взять через одинаковые интервалы времени и выполнить необходимые преобразования, выражения для коэффициентов примут вид

 

.                                (16)

 

Похожими зависимостями коэффициенты квадратного уравнения связаны со своими корнями. Этот факт позволяет составить следующее уравнение

 

, где .

 

Искомые времена запаздывания получаются при помощи выражений

 

.                                             (17)

 

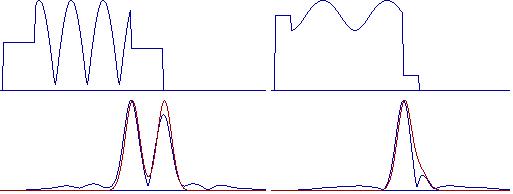
На рисунках 2, 3 показаны модули огибающих несжатых импульсов (верхние части рисунков) и сжатых (нижние части рисунков). Эти огибающие показаны синим цветом. Красным цветом показана аппроксимирующая функция.

 

 

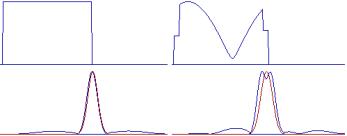
                                           а)                                               б)

Рисунок 2 – Огибающая ЛЧМ сигнала и экспоненциальной аппроксимирующей функции

На рисунке 2а представлена одноцелевая ситуация. На рисунке 2б показана огибающая сигналов двух источников соизмеримой интенсивности и малым взаимным рассогласованием.

 

 

а)                                               б)

Рисунок 3 – Огибающая ЛЧМ сигнала и экспоненциальной аппроксимирующей функции

На рисунке 3а показаны аналогичные огибающие для сигналов соизмеримой интенсивности при большом рассогласовании, а на рисунке 3б для сигналов различной интенсивности.

Анализируя представленные результаты, можно сделать вывод, что даже визуальная оценка точности аппроксимации показывает, что удовлетворительной она оказывается только для односигнальной ситуации.

Результаты моделирования процесса измерения дальностей двух целей при подобной аппроксимации огибающей положительный эффект дали только для случая соизмеримых амплитуд источников переизлучения и высоких отношений сигнал/шум.

Еще одним существенным недостатком подобной аппроксимации является то, что отсчеты для измерения обязательно должны быть на равноудаленных расстояниях друг от друга (в противном случае уравнения не решаются в радикалах). Это требование снижает гибкость алгоритма, а в некоторых случаях приводит к его неработоспособности.

При использовании второго типа аппроксимации были получены более высокие результаты, но точностные характеристики все равно оказались недостаточными для практического использования рассматриваемых алгоритмов.

Крупным недостатком рассматриваемого способа является то, что для составления системы уравнений необходимы напряжения, измеренные в соседних зондированиях. Это приводит к тому, что при больших скоростях цели ее перемещение за интервал зондирования оказывается существенным и вносит дополнительные ошибки в измерение дальности.

Учитывая то, что измерительный алгоритм предназначен для измерения координат не более, чем двух целей, последний недостаток можно устранить за счет того, что в системах уравнений (8) использовать не комплексные напряжения соседних импульсов, а квадратурные составляющие одного и того же импульса

 

.

 

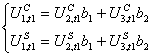Дальнейшая обработка сигнала остается неизменной, но ошибки за счет перемещения цели за интервал зондирования устраняются.

Для снижения погрешностей аппроксимации, кроме перечисленных в исходных данных были разработаны измерительные алгоритмы для аппроксимаций огибающей вида  и . Последняя аппроксимация оказалась достаточно точной, что позволило значительно улучшить точностные характеристики измерительного алгоритма.

Но, тем не менее, при существенных отличиях в амплитудах сигналов (по результатам моделирования больших 20 дБ) точность измерения дальности источника меньшей интенсивности оказалась недостаточно высокой.

 

4.     Метод измерения дальности, основанный на компенсации сигнала цели

большой интенсивности

 

В ходе исследования было выяснено, что наиболее эффективным и простым в реализации оказался метод измерения дальности источников сигналов различной интенсивности, принцип действия, которого основан на компенсации сигнала мощного источника [5].

Пусть принятый сигнал образован одним источником переизлучения и на огибающей сжатого ЛЧМ импульса произведена выборка, состоящая из двух отсчетов

 

.                                            (18)

 

Получим коэффициент, представляющий собой отношение модулей этих напряжений

 

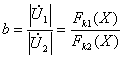.                                                     (19)

 

Из выражения (19) видно, что указанный коэффициент так же, как и в рассматривавшемся выше методе, не зависит от амплитуды источника переизлучения. Над квадратурными составляющими выборки проделаем следующую операцию

 

.                                                  (20)

 

Если в выражение (20) подставить значения напряжений из (18), получим

 

.

 

Иными словами, в случае наличия одиночного источника, приведенный алгоритм позволяет скомпенсировать его сигнал. Рассмотрим теперь ситуацию, когда входной сигнал образован двумя источниками переизлучения. Напряжения для различных рассогласований в этом случае будут выглядеть

 

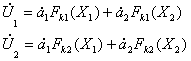.                                            (21)

 

Коэффициент, представляющий собой отношение модулей этих напряжений примет вид

 

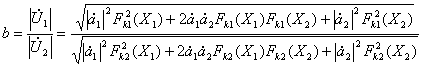 .               (22)

 

Очевидно, что если над квадратурными составляющими напряжений (21) проделать операцию, аналогичную (20), то компенсации сигнала в данном случае не произойдет. Рассмотрим, чему будут равны остатки величин ZС и ZS для ситуации, когда к примеру . Если второй отсчет взять вблизи пикового значения огибающей сжатого сигнала, то окажется, что , а . При этом условии выполнится приблизительное равенство

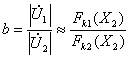,                                                 (23)

 

причем b всегда меньше 1. Если подставить b в выражения для ZС и ZS, получим

 

 

,

 

 

и, учитывая сделанные допущения,    .

Таким образом, рассмотренный алгоритм, который по сути представляет собой одноканальный алгоритм компенсации активной помехи, но трансформированный во временную область, позволяет выделить сигнал более слабого источника на фоне более сильного.

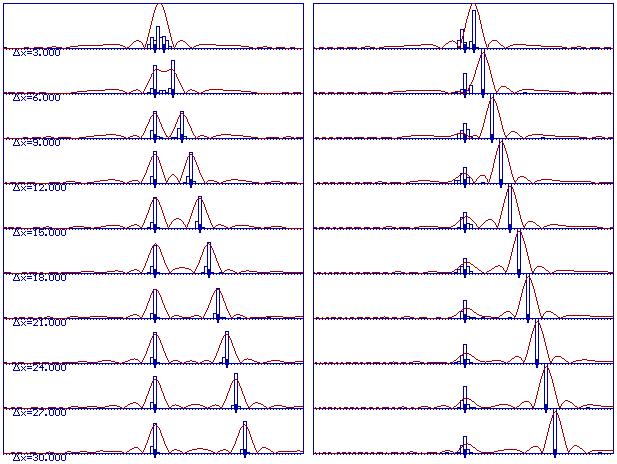
Для подтверждения работоспособности предлагаемого алгоритма было выполнено математическое моделирование процесса измерения дальности двух источников в следующих условиях: f0=12 МГц, 1/DT=24 МГц, S=128, Df=3 МГц, sш=1, амплитуда источника меньшей интенсивности =1. Амплитуды источников флуктуировали с sа=10% от номинальных значений. Результаты приведены в виде гистограмм. На горизонтальных осях указано количество отсчетов, составляющее расстояние между источниками переизлучения. Красным цветом показана огибающая сжатого сигнала. Рисками показано истинное положение целей.

 

а)                                                                          б)

Рисунок 4 – Результаты измерения дальностей двух целей при соотношении

их амплитуд 0 дБ (а) и 14 дБ (б).

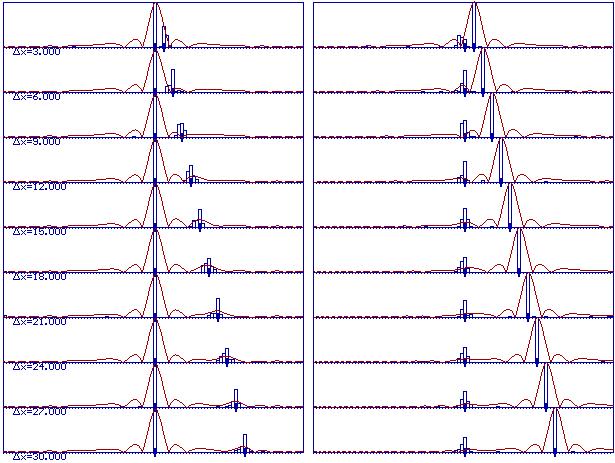
а)                                                                          б)

Рисунок 5 – Результаты измерения дальностей двух целей при соотношении

их амплитуд 20 дБ (а) и 30 дБ (б).

 

Результаты, приведенные на рисунках позволяют убедиться в том, что предложенный алгоритм позволяет измерить дальность до слабой цели на фоне более мощной в ситуациях, когда сигнал этой цели замаскирован боковыми лепестками цели большей интенсивности.

Разработанный алгоритм может быть использован устройством распознавания положения истинной цели (слабый сигнал) относительно ловушки (более сильный сигнал) при анализе огибающей на входе автодальномера станции сопровождения цели существующих ЗРК с телеуправлением ЗУР. Определение положения истинной цели относительно сопровождаемого автодальномером положения кажущегося центра групповой сосредоточенной цели позволит ввести поправки в команды управления ЗУР, обеспечивая её вывод на самолет.

 

Литература

 

1. Варюхин В. А. Основы теории многоканального анализа. Киев, ВА ПВО СВ им. Василевского А.М., 1993, 172 с.

2. Марплмл С.Л. Цифровой спектральный анализ и его приложения. - М.: Мир, 1990.

3. Дрогалин В. В., Меркулов В. И., Родзивилов В. А., Федоров И. Б., Чернов М. В. Алгоритмы оценивания угловых координат источников излучений, основанные на методах спектрального анализа. Радиолокация и радиометрия, № 1, 1999.

4. Дрогалин В. В., Татарский Б. Г., Чернов М. В. Алгоритмы пространственно-временной обработки сигналов при одновременной пеленгации неизвестного изменяющегося во времени числа постановщиков помех. М. ВВИА им. Н.Е. Жуковского, 1997.

5. Царьков Н. М. Многоканальные радиолокационные измерители. М. Сов. радио, 1980.

5.     Курикша А. А. Оценка числа и параметров компонент сигнала при наличии шумов. - Радиотехника и электроника. – 1984. - № 9.

 

Академия войсковой ПВО Вооруженных Сил РФ

им. Маршала Советского Союза А.М. Василевского,

г. Смоленск

 Поступила в редакцию 29.01.2013.