Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 12. -
Вып. 1. - 2013. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/TITL-37.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/cont.htm
УДК
621.372.67
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ АНТЕННОЙ
РЕШЕТКИ С УМЕНЬШЕННОЙ РАДИОЛОКАЦИОННОЙ ЗАМЕТНОСТЬЮ
Ó
2013 г. Калашников А. В.
В данной работе изложен порядок решения
дифракционной задачи для совмещенной антенной решетки с уменьшенной
радиолокационной заметностью. Решение основано на использовании теоремы Флоке
для бесконечных антенных решеток.
Ключевые слова: антенная решетка,
теорема Флоке.
В настоящее время все большее внимание уделяется проблеме снижения радиолокационной заметности различных объектов. В частности, эта проблема касается и антенных систем. Наибольший интерес вопросы рассеяния электромагнитной энергии антеннами представляют после реализации в США программы «Стелс», в результате которой применение различных поглощающих материалов и покрытий позволило значительно уменьшить эффективную поверхность рассеяния (ЭПР) летательных аппаратов в радиолокационном диапазоне длин волн. Необходимо заметить, что ЭПР таких летательных аппаратов стала определяться главным образом отражением от антенн. Как известно, правильно сконструированная и хорошо согласованная с нагрузкой и внешним пространством антенна в рабочем диапазоне частот имеет малую ЭПР. Однако при облучении антенны зондирующим сигналом другого частотного диапазона ее ЭПР может достигать больших величин (до сотен квадратных метров), причем это особенно характерно для апертурных антенн. Поэтому при проектировании объектов с низкой радиолокационной заметностью в определенном частотном диапазоне необходимо знать характеристики рассеяния антенн, что делает необходимым решение для них дифракционной задачи.
Одним из путей уменьшения радиолокационной заметности плоских антенных решеток является введение в нее компенсационных излучателей для формирования электромагнитного поля, равного по амплитуде и противофазного отраженному от антенной системы. Такая апертура представляет собой антенную решетку, в которой основная решетка, выполняющая функции по предназначению, совмещена с компенсационной. Для уменьшения радиолокационной заметности антенной системы в нерабочем диапазоне частот компенсационные излучатели должны функционировать на частотах, отличных от рабочей частоты основных излучателей. В качестве объекта исследования выбрана эквидистантная совмещенная волноводная антенная решетка с равномерным амплитудным распределением. Для учета взаимного влияния волноводных излучателей разных частотных диапазонов использована модель бесконечной антенной решетки, основанная на теореме Флоке [1]. Так, исследуемая антенная система дополняется до бесконечной и представляет собой двоякопериодическую структуру с равномерным амплитудным и линейно изменяющимся по фазе возбуждением. Электромагнитное поле в такой антенной системе повторяется от периода к периоду решетки, что позволяет ограничиться рассмотрением одного периода решетки, или ячейки Флоке. Ячейка Флоке совмещенной волноводной антенной решетки содержит основной волновод и короткозамкнутый компенсационный волновод, который имеет в своем составе управляемые фазовращатель и усилитель для управления полем рассеяния. Поля внутри волноводов описываются известными волноводными функциями, а в области свободного пространства – гармониками Флоке [1, 2].
Решение дифракционной задачи осуществляется в несколько этапов.
На первом этапе рассматривается структура, приведенная на рис. 1.
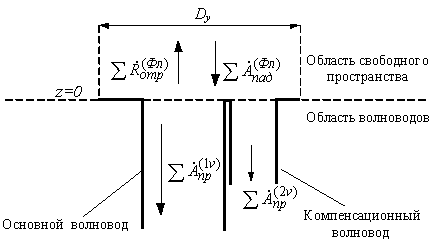
Рис. 1 – К
первому этапу математического моделирования дифракционной задачи.
Так, на элемент
совмещенной волноводной антенной решетки из области свободного пространства
падает спектр гармоник Флоке с комплексными амплитудами падающих волн 
. Часть энергии в силу несогласованности тракта приема
отражается обратно в пространство с комплексными амплитудами отраженных волн 
, а часть энергии проходит в основной и компенсационный
волноводы. Комплексные амплитуды прошедших волн соответственно обозначены для
основного волновода 
и для компенсационного волновода – 
. Принимая, что
возбуждение элемента решетки осуществляется волной основного типа единичной
амплитуды, и используя проекционные соотношения на границе раздела сред (z=0), а
также свойства ортогональности вектор-функций была составлена система линейных
алгебраических уравнений:
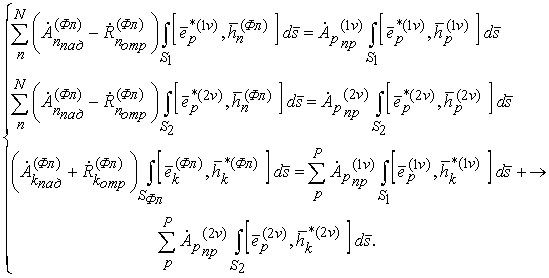
В результате решения этой системы найдены неизвестные комплексные амплитуды отраженных и прошедших в волноводы волн.
На втором этапе
анализируется структура, приведенная на рис. 2.
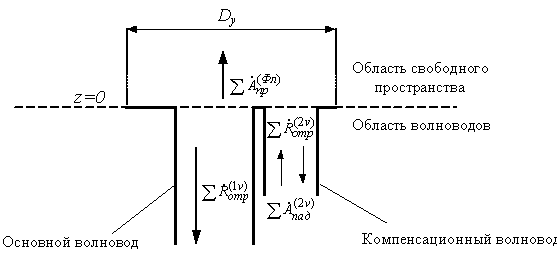
Рис. 2 – Ко второму этапу математического моделирования дифракционной
задачи
Здесь
рассматривается возбуждение волной основного типа единичной амплитуды
компенсационного волновода. Часть энергии на границе раздела сред отражается
обратно в силу несогласованности тракта с комплексными амплитудами отраженных
волн 
, другая часть в силу взаимного влияния возбуждает основной
волновод с комплексными амплитудами 
. Оставшаяся часть энергии с комплексными амплитудами прошедших
волн 
проходит в пространство.
В итоге
получается система линейных алгебраических уравнений, в результате решения
которой найдены неизвестные комплексные амплитуды прошедших и отраженных волн:
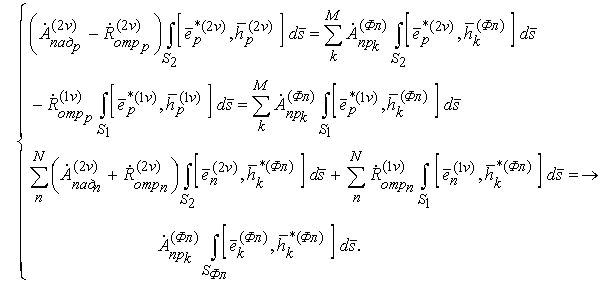
При рассмотрении
процесса дифракции на совмещенной решетке в динамике возбуждение
компенсационного волновода будет осуществляться с комплексной амплитудой,
отличающейся от единичной на некоторый комплексный коэффициент 
, который определяется на третьем этапе решения задачи дифракции
с учетом многократного переотражения волн между границей раздела сред и
коротким замыканием в компенсационном волноводе. Кроме того, на данном этапе
осуществляется выбор характеристик управляемого усилителя и управляемого
фазовращателя, а также определяется связь решений, полученных на первом и
втором этапах. Фазовращатель моделируется с помощью изменения глубины l до
короткого замыкания в компенсационном волноводе. Комплексный коэффициент 
учитывает и граничные
условия на коротком замыкании в компенсационном волноводе. На рис. 3. приведена
структура составляющих электромагнитного поля при решении граничной задачи на
коротком замыкании компенсационного волновода.
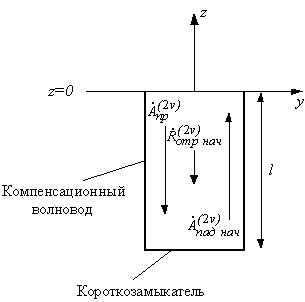
Рис. 3 – К
третьему этапу математического моделирования
Комплексная
амплитуда 
, определенная на первом этапе, связывается с начальной
комплексной амплитудой падающей волны 
и найденной на втором
этапе комплексной амплитудой 
.
Комплексная
амплитуда падающей волны на втором этапе моделирования в плоскости z=0 равна 
и ее величина по
условию равна единице. В силу того, что возбуждение компенсационного волновода
осуществляется из внешнего пространства с комплексной амплитудой, отличающейся
от единичной на некоторый комплексный коэффициент 
, при совмещении двух
решений комплексная амплитуда падающей волны равна 
. Так как решаемая задача линейна, найденные комплексные
амплитуды отраженных волн 
и прошедших волн 
необходимо умножить
на комплексный коэффициент 
.
Поиск значения
коэффициента 
представляет собой
итерационную процедуру, вызванную многократным отражением волны, прошедшей в компенсационный
волновод от короткого замыкания и границы раздела «компенсационный волновод –
свободное пространство»:
.
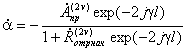В этих
выражениях 
– постоянная
распространения в компенсационном
волноводе, а 
– расстояние от
раскрыва до короткого замыкания.
При введении
управляемого усилителя с коэффициентом усиления 
выражение для
комплексного коэффициента 
принимает вид
.
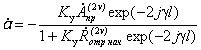Комплексные
амплитуды гармоник Флоке, прошедших в свободное пространство, на втором этапе
необходимо умножить на этот коэффициент 
, что определяет связь решений первого и второго этапов и
баланс мощности.
На четвертом
этапе для строгого решения дифракционной задачи необходимо найти комплексные амплитуды прошедших гармоник Флоке,
определяющих отражение от фазовращателя основного волновода, что может объясняться
отличием частотного диапазона работы этого фазовращателя и частоты падающей на
антенную решетку электромагнитной волны. Необходимо заметить, что коэффициент
отражения индивидуален для каждого вида фазовращателей и определяется опытным
путем для конкретной антенной системы.
На
заключительном, пятом, этапе моделирования дифракционной задачи определяется
комплексная суммарная диаграмма обратного рассеяния ячейки Флоке, содержащей основной и компенсационный излучатели.
Так, коэффициент отражения ячейки Флоке
по мощности 
определяется отношением
квадрата модуля разности комплексных амплитуд гармоник Флоке с нулевыми
индексами, найденных на первом, третьем и четвертом этапах к квадрату модуля
комплексной амплитуды падающей гармоники Флоке на первом этапе:
.
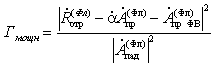В свою очередь
коэффициент отражения 
ячейки Флоке по амплитуде
равен
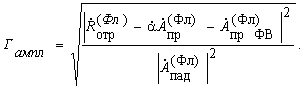
Нормированные
диаграммы обратного рассеяния ячейки Флоке по мощности и по амплитуде
определяются по формулам
,
.
Для нахождения
диаграммы обратного рассеяния волноводной антенной системы конечных размеров
необходимо диаграмму обратного рассеяния ячейки Флоке умножить на соответствующий
множитель решетки.
Подбором коэффициента усиления управляемого усилителя
и расстояния 
от раскрыва ячейки
до короткозамыкателя (параметров управляемого фазовращателя) осуществляется
уменьшение коэффициента отражения в заданных направлениях.
Литература
1. Амитей Н., Галиндо В., Ву Ч. Теория и анализ фазированных антенных решеток. М., Мир, 1974. – 455 с.
2. Воскресенский Д. И., Кременецкий С. Д., Гринев А. Ю., Котов Ю. В. Автоматизированное проектирование антенн и устройств СВЧ. М., Радио и связь, 1988. – 240 с.
MATHEMATICAL MODELLING
ANTENNA ARRAY WITH REDUCED RADAR
VISIBILITY
Kalashnikov A. V.
In
this work it is exposed an order of decision of a diffraction job for a compatible
antenna array with a reduced radar visibility. The job is established with
Floke’s theorem help for the infinite antenna array.
Key words: diffraction job for a compatible antenna, Floke’s
theorem.
Академия
войсковой ПВО Вооруженных Сил РФ
им.
Маршала Советского Союза А.М. Василевского,
г. Смоленск
Поступила в редакцию 29.01.2013.