Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 12. -

Вып. 1. - 2013. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/TITL-37.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/cont.htm

УДК 51-76

ОПТИМИЗАЦИЯ ФОРМЫ ЭРИТРОЦИТА В СООТВЕТСТВИИ С ДАННЫМИ АТОМНО-СИЛОВОЙ МИКРОСКОПИИ

Ó 2013 г. Нагорнов Ю. С.¹, Жиляев И. В.²

(nagornov.doc)

В работе предложена математическая модель эритроцита, позволяющая рассчитать упругие свойства мембраны и его морфологию. Модель представляет эритроцит в виде однородного упругого тела с упругостью, зависящей от расстояния до центра симметрии эритроцита. Расчет упругих свойств выполнен при помощи оптимизации функционала, учитывающего минимум энергии деформации и максимальное соотношение площади к объему. Расчет энергии деформации проводился методом конечных элементов, а оптимизация при помощи генетического алгоритма. Проведено сравнение расчетных данных с данными атомно-силовой микроскопии, что позволило сделать вывод о состоятельности модели и ее развитии. Кроме этого модель позволяет предположить изменение тонкой структуры цитоскелета мембраны в зависимости от расстояния до центра эритроцита, что может быть связано с концентрацией белка полосы 3 или с размерами ячеек филаментной сети.

Ключевые слова: атомно-силовая микроскопия, метод конечных элементов, метод минимизации функционала, метод оптимизации, эритроцит, мембрана цитоскелета.

Введение

Эритроциты - высокоспециализированные клетки крови, выполняющие газотранспортную функцию переноса кислорода из лёгких к органам и тканям, а диоксида углерода - в обратном направлении. Зрелые эритроциты человека лишены ядра и органелл и имеют форму двояковогнутого диска с максимально высоким отношением площади к объёму, что обеспечивает наиболее оптимальный газообмен. Особая форма эритроцитов увеличивает их диффузионную поверхность с одновременным уменьшением диффузного расстояния [1]. Транспорт кислорода обеспечивается гемоглобином, на долю которого приходится около 98% массы белков цитоплазмы эритроцитов.

Особенности цитоскелета и строения клеточной мембраны двояковогнутых эритроцитов позволяют им претерпевать значительные деформации при прохождении через узкие изогнутые капилляры с последующим восстановлением формы. Кроме того, форма красных кровяных клеток зависит от осмотического давления в эритроцитах и в плазме крови, а также от состояния цитоскелета мембраны эритроцитов, влияющего на упругие свойства оболочек красных кровяных телец [1,2]. В настоящей статье делается попытка ответить на вопрос: почему эритроцит приобретает форму двояковогнутого диска при условии однородности содержимого эритроцита? Какие факторы влияют на форму эритроцита и его упругие свойства? Для ответа на эти фундаментальные вопросы необходимо привлечь данные о цитоскелете клеточной мембраны эритроцитов.

В последнее время наиболее интересные и полные экспериментальные данные о структуре эритроцита и строении цитоскелета были получены методами атомно-силовой микроскопии (АСМ) [2-5]. Применяя различные режимы АСМ, можно измерять ригидность или упругость, вязкость, адгезию и другие свойства мембран клеток [3]. Работа АСМ- микроскопа основана на измерении сил взаимодействия кантилевера и поверхности клеток. Перемещаясь относительно поверхности и реагируя на силовое взаимодействие, АСМ регистрирует ее рельеф. На основании прибора укреплен цилиндр, в котором находится сканер из пьезоэлектрической керамики, изменяющей свои размеры при приложении электрического поля. В верхней части цилиндра крепится исследуемый образец, который сканер может перемещать в трех взаимно перпендикулярных направлениях. В горизонтальной плоскости образец сканируется по строкам: пройдя одну, он смещается на следующую строчку.

Наиболее интересные данные атомно-силовой микроскопии о мембране эритроцита были получены в работах [2,3], где указывалось, что коэффициент упругости (коэффициент ригидности или модуль Юнга) мембраны эритроцитов в норме равен 1,4-1,7 кПа [2], при этом по данным другой работы [3] ригидность в центре и на краю эритроцита отличается на 25-40%. Прямое наблюдение методами АСМ тонкой структуры филаментной сети мембраны эритроцита позволила определить размер её ячеек в диапазоне 50-70 нм [4].

Существуют также и методические сложности при АСМ измерениях, например, при использовании метода мазка происходит высыхание эритроцита на воздухе и он теряет свой объем более чем в 2 раза, сохраняя, тем не менее, исходные соотношения основных геометрических характеристик, что позволяет использовать АСМ для морфологической оценки клеток крови [5-7]. В работе [4] методами АСМ и Рамановского рассеяния была показана корреляция между толщиной клеток крови и содержанием в них гемоглобина, что связывалось с разрушением мембраны эритроцитов при различных состояниях и методах подготовки к измерениям.

Настоящая статья посвящена численному расчету оптимизации формы эритроцитов с целью оценки их упругих и морфологических свойств, исходя из экспериментальных данных, полученных атомно-силовой микроскопией.

1. Геометрическая и математическая модель эритроцита

На основе имеющихся данных о линейных размерах и физических константах эритроцита в пакете Comsol Multiphysics была построена осесимметричная конечно-элементная модель (рис.1). Данный пакет моделирования решает системы нелинейных дифференциальных уравнений в частных производных методом конечных элементов в одном, двух и трех измерениях. В модели геометрия эритроцита задается фигурой вращения в цилиндрических координатах вокруг прямой _, где ось r является осью абсцисс, а ось z – ординат. Верхняя граница области представляет собой три последовательно соединенные кривые Безье третьего порядка, каждая из которых представляется в виде:

,

где P₀, P₁, P₂ и P₃ – опорные точки, задающие координаты и направление кривой, а параметр t задает координаты точек на кривой.

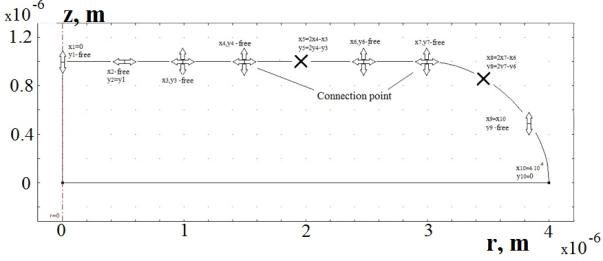
Рис 1. Геометрия модели эритроцита, заданной в цилиндрических координатах последовательно соединенными кривыми Безье.

Точки, определяющие кривые Безье, задаются по разному. Некоторые точки имеют две степени свободы и перемещаются в двух независимых направлениях, некоторые – только в одном направлении. Направления перемещения точек в процессе оптимизации показано на рис.1 стрелочками, координаты точек под номерами 5 и 8, показанных в виде крестиков, алгебраически определяются из соседних точек для того, чтобы геометрия поверхности была гладкой. Кроме этого на свободные перемещения точек накладываются естественные ограничения, предупреждающие наложение точек друг на друга и создание пересекающихся граней.

Плотность эритроцита в модели задается равной плотности крови, т.е. . Поскольку ригидность в центре и на краю эритроцита отличается [3] модуль упругости в модели задается функцией от координаты абсцисс:

_,

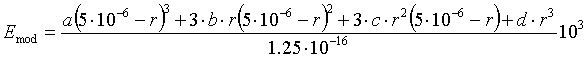где параметры a и d задаются таким образом, чтобы ограничить перепад значений функции в пределах от 1.0 до 1.6 кПа для значений , а параметры b и c определяют изгибы кривой. Кривая является также достаточно гладкой, чтобы при расчете исключить появление изломов поверхности, обусловленных упругостью.

Описанная модель решается модулем Stress-Strain программного пакета Comsol Multiphysics. В процессе расчетов определяются механические напряжения и деформации тела, его линейные размеры, а также его внутренняя потенциальная энергия деформации. На верхнюю границу эритроцита действует равномерно распределенное давление, величина которого задается параметром, в нашем случае, изменяемом в диапазоне от 500 до 2000 Па.

Полный алгоритм расчета выглядит следующим образом. На каждом шаге расчета происходил экспорт полученной конечно-элементной модели в среду Matlab и определение функционала оптимизации. При этом полученная на предыдущем шаге конечно-элементная модель экспортируется в программную среду Matlab в виде скрипта. Экспорт обусловлен необходимостью непосредственного доступа к координатам ряда точек кривых Безье для возможного изменения формы расчетной области, а также возможностями оптимизационных модулей Matlab. Результатом работы полученной функции является значение функционала:

_,

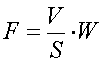где V – объем фигуры вращения, S – ее площадь, W – интеграл по объему потенциальной энергии деформации, который рассчитывается считая что сжатие происходит по линейному закону.

Функционал оценивает модель с точки зрения минимальной потенциальной энергии деформации и наибольшего соотношения площади фигуры к ее объему. Данный функционал введен для последующего внедрения его в генетический алгоритм. Для оптимизации был выбран генетический алгоритм, реализованный в модуле OptimTool пакета Matlab.

2. Результаты расчета оптимизации морфологии и упругих свойств эритроцита при помощи генетического алгоритма

Расчет производился при помощи генетического алгоритма до тех пор, пока изменения в следующем поколении в функционале F не стали менее 2-3%. Как правило, для этого было необходимо более 100 поколений. На рис.2 представлена зависимость модуля упругости E_mod мембраны от расстояния до центра эритроцита, построенная по оптимизированным параметрам b и c. Видно, что зависимость имеет два участка – до 2 мкм резкое увеличение модуля и после 2 мкм плавное увеличение, что может быть связано с морфологией эритроцита, представленной на рис.3.

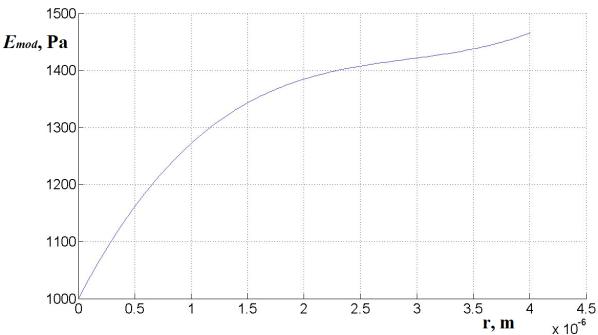
Рис.2. Зависимость модуля упругости мембраны от расстояния до центра эритроцита.

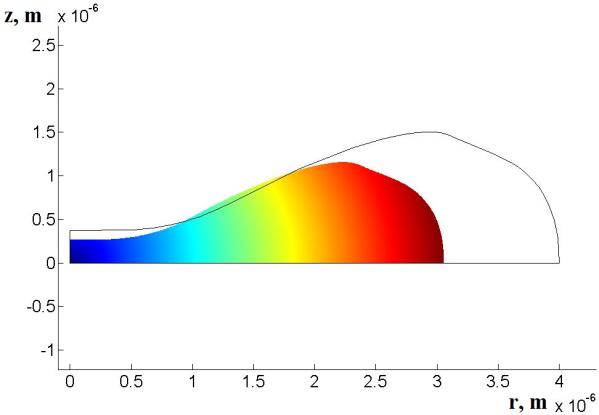
Рис.3. Морфология эритроцита в соответствии с расчетами по оптимизации в отсутствии давления (контур) и при давлении 2000 Па (заливка).

Из рис.3 видно, что расчетная форма близка к форме эритроцита как по размерам в длину (5-7 мкм) и высоту (2-3 мкм), так и по морфологии. Несколько отличий можно увидеть в расчетной форме эритроцита. Так участок в районе 2.2-2.4 мкм (3-3.2 мкм для контура) имеет перегиб, не связанный с упругими характеристиками мембраны. Для проверки наличия этого перегиба были проведены дополнительные расчеты, и количество поколений увеличено в 5-10 раз для различных давлений. Как показал расчет во всех случаях перегиб оставался.

Для объяснения этого феномена обратимся за результатами работы [8], в которой изучалось влияние вирионов гриппа на тонкую структуру мембраны эритроцитов. На рис.4а показана тонкая структура мембраны в норме, особенности рельефа, наблюдаемые на мембране интерпретируются как спектриновый мембранный скелет [8]. На рис.4б можно увидеть, что воздействие вирусов влияет на мембрану эритроцитов, в частности, происходит размытие мембранного скелета. На рис.4в видны кластеры, регулярно наблюдающиеся на краю эритроцитов, взаимодействовавших с вирионами и не наблюдающиеся на нативных клетках. Авторы работы [8] не могут указать причины появления кластеров, однако их можно соотнести с нашими результатами и связать с перегибом в районе 2.2-2.4 мкм (рис.3), если предположить, что кластеры существуют в эритроцитах в любом состоянии, но проявляются только при воздействии вирусов. Таким образом, косвенно можно соотнести результаты расчета с экспериментальными данными атомно-силовой микроскопии.

Наиболее интересным представляется сравнение морфологии эритроцита, полученной в результате расчета и по данным АСМ. Для этого приведем данные АСМ для нормальных эритроцитов, не подвергнутых каким-либо воздействиям. На рис.5 представлен поперечный разрез эритроцита в норме, полученного полуконтактным методом АСМ.

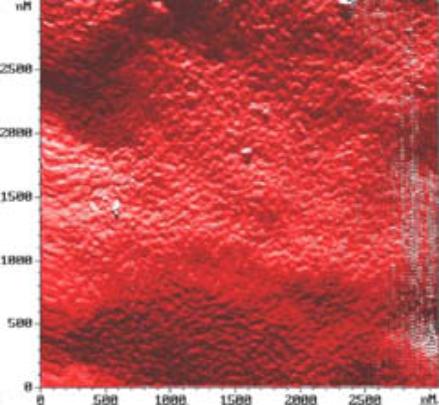
а

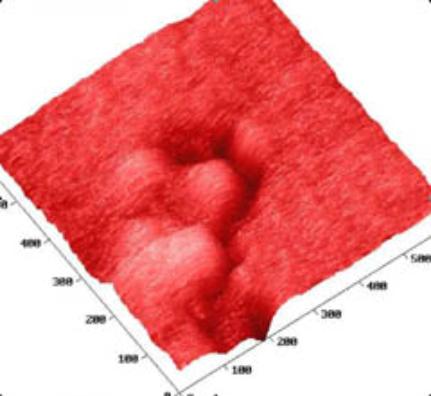
b

c

Рис. 4. Тонкое строение мембраны на АСМ сканах эритроцитов [8]:

a – контрольный образец. Мембрана имеет классическое строение. Размер скана 2.5 на 2.5 мкм.

b – нарушения рельефа, связанные с действием вирионов. Размер скана 500 на 500 нм.

с – кластеры, регулярно наблюдающиеся на краю эритроцитов, взаимодействовавших с вирионами и не наблюдающиеся на нативных клетках. Размер скана 2.5 на 2.5 мкм.

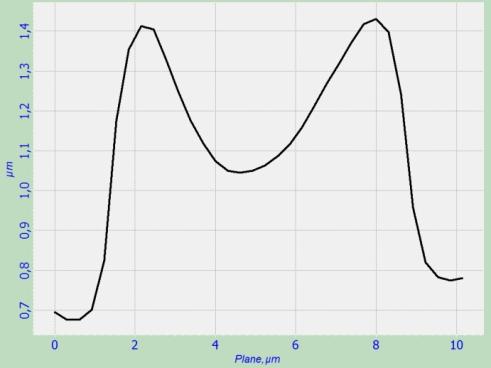
Рис.5. Поперечный разрез эритроцита в норме, полученного полуконтактным методом атомно-силовой микроскопии.

Сравнение форм эритроцитов по данным атомно-силовой микроскопии и расчетной модели необходимо проводить с учетом изменения формы при осаждении эритроцита на подложку. Действительно, эритроцит в модели и в физическом растворе является полностью симметричным объектом. При осаждении на подложку возникают два эффекта, изменяющие форму эритроцита. Во-первых, это прилипание мембраны эритроцита на подложку и связанное с этим «растекание» с видимым удлинением формы. Во-вторых, впадины эритроцита сверху и снизу по причине прилипания к поверхности подложки превращаются в одну впадину с глубиной, равной сумме двух впадин эритроцита, не осажденного на подложку.

С учетом сделанных замечаний проведено сравнение морфологии эритроцитов, полученной в расчетах и при измерении методами АСМ. На рис. 5 представлен эритроцит в норме, имеющий глубину впадины 0.4 мкм, диаметр 7-8 мкм и ширину 0.7 мкм. Необходимо отметить, что ширина эритроцита в АСМ существенно занижается из-за высыхания и процесса измерения, в котором на эритроцит оказывается механическое воздействие. В результате наблюдаемый объем и толщина эритроцита уменьшаются в несколько раз.

Данной форме соответствует модель эритроцита, представленная на рис. 3 с глубиной впадины равной 1.4 мкм, диаметром 6 мкм, шириной 2 мкм. Поскольку модель не учитывает процессы адгезии и прилипания эритроцита к поверхности, происходящие при измерении методами АСМ, данные в расчетах отличаются от данных АСМ. При этом в расчете и эксперименте АСМ сохраняются пропорции, например, отношение длины от центра эритроцита до его вершины к расстоянию от вершины до края в обоих случаях равно 3 к 1.

Необходимо сделать несколько замечаний по модели и сравнении полученных расчетных данных с экспериментальными. Модель эритроцита исходит только из предположения о зависимости упругости мембраны от расстояния до центра, на основании проведенных расчетов видно, что модель на качественном уровне описывает изменение морфологии в зависимости от состояния мембраны.

Предположение о зависимости упругости мембраны от расстояния до центра, положенное в основу модели, имеет с одной стороны экспериментальное подтверждение в ряде работ по атомно-силовой микроскопии [2,3], с другой стороны имеет важное следствие. Поскольку модель косвенно подтверждает наличие изменений упругости по поверхности мембраны, возникает естественный вопрос, чем обусловлена эта зависимость упругости. Учитывая, что цитоскелет мембраны эритроцитов состоит из филаментной сети, образованной белком спектрина, а также то, что за упругие свойства мембраны в основном отвечает связующий белок полосы 3, данные моделирования свидетельствуют в пользу следующего предположения.

В центре мембраны эритроцита упругие свойства эритроцита примерно в 1,5 меньше, чем на краю, что может быть обусловлено меньшей концентрацией белка полосы 3, а также более разряженной по сравнению с краем эритроцита, сеткой цитоскелета. Атомно-силовая микроскопия позволяет определять тонкую структуру цитоскелета мембраны [8,9], по данным которой структура состоит из ячеек с размерами 50-70 нм. Сложность определения рельефа такого масштаба на биологических объектах до сих пор не позволила определить степень изменения тонкой структуры по поверхности мембраны. Таким образом, в рамках модели стоит задача определения изменений тонкой структуры мембраны по поверхности эритроцита с удалением от его центра, с другой стороны изменение концентрации белка полосы 3.

Заключение

В работе рассматривается модель эритроцита, позволяющая рассчитать упругие свойства мембраны и его морфологию. Поскольку известно, что эритроцит состоит из гемоглобина, его можно представить как однородное упругое тело. При этом из экспериментальных данных атомно-силовой микроскопии известно [3,9], что упругость мембраны зависит от расстояния до центра симметрии эритроцита. В опоре на два этих факта в предложенной модели проводится оптимизация функционала, учитывающего минимум энергии деформации и максимальное соотношение площади к объему. При этом расчет энергии деформации проводился методом конечных элементов. Сравнение расчетных данных с данными атомно-силовой микроскопии позволило сделать вывод о состоятельности модели. Можно предположить, что изменение упругих свойств является следствием зависимости тонкой структуры цитоскелета мембраны от расстояния до центра эритроцита, что может быть связано с концентрацией белка полосы 3 или с размерами ячеек филаментной сети.

Литература

1. Физиология человека: учебник/под ред. В. М. Покровского, Е. Ф. Коротько.-2-е изд., перераб. и доп. М.: «Медицина», 2007. 656с.

2. Арсланова Д. Р., Абакумова Т. В. и др. Влияние фемтосекундного лазерного излучения на эритроциты IN VITRO // Лазерная медицина, 2011. Т.15. № 2. С. 215-215.

3. Дрозд Е. С., Чижик С. А., Константинова E.Э. Атомно-силовая микроскопия структурно-механических свойств мембран эритроцитов // Российский журнал биомеханики, 2009. Т.13.- № 4 (46). С. 22–30.

4. Asghari-Khiavi M.,  Wood B. R.,  Mechler A.,  Bambery K. R., Buckingham D. W., Cooke B. M. and McNaughton D. Correlation of atomic force microscopy and Raman micro-spectroscopy to study the effects of ex vivo treatment procedures on human red blood cells // Analyst, 2010. 135. 525-530.

5. Dulińska I., Targosz M. et al. Stiffness of normal and pathological erythrocytes studied by means of atomic force microscopy // J Biochem Biophys Methods, 2006 Mar 31. 66(1-3):1-11.

6. Nowakowski R., Luckham P. Imaging the surface details of red blood cells with atomic force microscopy // Surface and Interface Analysis, 2002. V. 33, Issue 2. 118–121.

7. O'Reilly M., McDonnell L., O'Mullane J. Quantification of red blood cells using atomic force microscopy // Ultramicroscopy, 2001. Jan.-86(1-2):107-12.

8. Zaitsev B. N., Durymanov A. G., Generalov V. M. Atomic Force Microscopy of the Interaction of Erythrocyte Membrane and Virus Particles. Proc. Intern. Workshop "Scanning Probe Microscopy-2002", p. 211-213. Nizhny Novgorod, 03.03-06.03.2002.

9. Гущина Ю. Ю., Плескова С. Н., Звонкова М. Б. Исследование различий морфологических параметров клеток крови человека методом сканирующей зондовой микроскопии // Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2005. №1. С. 48–53.

OPTIMIZATION OF ERYTHROCYTE FORM ACCORDING TO DATA OF ATOMIC FORCE MICROSCOPY

Nagornov Yu. S.¹, Zhilyaev I. V.²

The paper presents a mathematical model of the erythrocyte, which allows to calculate the elastic properties of the membrane and its morphology. The model represents the erythrocyte as a homogeneous elastic body with elastic, depending on the distance to the center of symmetry of the erythrocyte. The calculation is made of the elastic properties by optimizing functional, taking into account the minimum strain energy and the maximum ratio of surface to volume. The calculation of the strain energy carried by finite element method, and optimization using genetic algorithms. The comparison of the calculated data with atomic force microscopy, the conclusion is drawn on consistency of model and its development. Additionally, the model allows to assume variation of the fine structure of the cytoskeleton of the membrane, depending on the distance to the center of the erythrocyte, which may be due to the concentration of the protein band 3 with mesh size or filament network.

Key words: atomic force microscopy, finite element method, functional minimization, optimization method, erythrocyte, membrane cytoskeleton.

Работа выполнена при поддержке

ФЦП «Научные и научно-педагогические кадры

инновационной России»

на 2009-2013 годы (соглашение № 14.B37.21.0228).

Нагорнов Юрий Сергеевич – к.ф.-м..н., доцент, снс научно-исследовательской части Тольяттинского государственного университета, докторант.

к.т. 89603738857.

Жиляев Игорь Витальевич – аспирант, Южный федеральный университет.

¹ФГБОУ ВПО «Тольяттинский государственный университет», Тольятти, Россия (445667, г. Тольятти,

Самарской обл., ул. Белорусская, 14),

e-mail: rq-georg@rambler.ru

²ФГАОУ ВПО «Южный федеральный университет», Ростов-на-Дону,

Россия (344006, г. Ростов-на-Дону, ул. Б.Садовая, 105/42), Zhilyaev@mail.com

¹Togliatti State University, Togliatti,

Russia (445667, Togliatti, Samara region. St. Belarus, 14),

e-mail: rq-georg@rambler.ru

²Southern Federal University, Rostov-on-Don,

Russia (344006, Rostov-on-Don, st. B.Sadovaya, 105/42), Zhilyaev@mail.com

Поступила в редакцию 2.03.2013.