Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 12. -
Вып. 1. - 2013. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/TITL-37.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/cont.htm
УДК 623.4
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ВОЗМОЖНОСТИ
ДОСТИЖЕНИЯ ТРЕБУЕМОГО ПОРЯДКА АСТАТИЗМА
КОМПЛЕКСИРОВАННЫХ СИСТЕМ СОПРОВОЖДЕНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ
Ó 2013 г.
Савицкий Ф. Л., Васильченко О. В.
В работе представлено теоретическое обоснование возможности достижения
у комплексированных систем автоматического сопровождения воздушных объектов требуемого
порядка астатизма. за счет компенсации составляющих динамической ошибки
сопровождения, при организации оптимальной связи между комплексируемыми локационными
каналами.
Ключевые слова: комплексированные следящие системы, высокоскоростные малоразмерные
воздушные объекты, точность сопровождения, порядок астатизма.
Совершенствование автоматических
систем сопровождения является важной задачей, так как они находят широкое
применении в различных технических устройствах от систем управления воздушным
движением, до комплексов военного назначения, где от качества их работы зависит
жизнь человека. В последенее время наметилась устойчивая тенденция все большего
применения малой авиации в качестве транспортного средства личного пользования.
Между тем сложность автоматического
сопровождение малоразмерных воздушных объектов связана со значительным
увеличением их маневренных характеристик. Это связано со снижением дальности
обнаружения этих объектов радиолокационными системами автоматического сопровождения
этих объектов, что ведет к росту динамической ошибки их сопровождения.
Для достижения заданной точности сопровождения, как правило,
используются оптимальные (синтезированные при фиксированных характеристиках
процесса) следящие системы. Между тем автоматическим следящим системам
приходится функционировать в условиях априорной неопределенности характеристик
полезных воздействий, что делает эти системы неэффективными.
Наиболее эффективным способом преодоления априорной
неопределенности условий функционирования системы автоматического сопровождения
цели является построение системы, инвариантной (нечувствительной) или
квазиинвариантной (слабо чувствительной) к изменению этих условий.
Для достижения этого применяется способ уменьшения
ошибок слежения, применением связей от входной величины, при котором кроме
сигналов, являющихся функцией ошибки управления, используются также сигналы, зависящие
от задающих воздействий [1].
Однако для радиолокационных следящих измерителей
теорию инвариантности непосредственно использовать нецелесообразно, так как их
входным воздействием является смесь сигнала и помехи, и поэтому следящий измеритель при инвариантности
к полезному воздействию пропускает на выход без искажения также и мешающее
воздействие.
Между тем повышение точности системы сопровождения
воздушных объектов возможно за счет более полного (комплексного) использования
объективно имеющейся в ЗК локационной информации, в частности, радиолокационной
и оптической.
Анализ способов комплексного использования
измерительной информации, позволил сделать вывод, что инвариантность к
задающему воздействию следящей системы можно обеспечить путем комплексирования
ее с автономными измерителемя (датчиками) этих воздействий. Комплексирование
активно-пассивных локационных каналов может обеспечить независимость момента
коррекции ошибки системы сопровождения с помощью одного из измерителей
(датчиков), возможность получения более точной информации от нескольких
измерителей по сравнению с одним из них, а также повышение уровня помехозащищенности
(скрытности и помехоустойчивости) КЦ.
Повышение точности следящей системы и достижения ее
инвариантности осуществляется на основе комплексированных систем с введением дополнительной
информации в контур слежения ОК [2].
Обобщенная структура такой системы представлена на рисунке 5, на
котором S(p), W(p) – соответственно ОКП пеленгационного устройства (ПУ) и
исполнительного устройства (ИУ) ОК КС, Н(р)
– ОКП j-го корректирующего канала (КК) КС.
Динамика системы, представленной на рисунке 5, описывается системой
уравнений (3), где 
. Так как решается задача обеспечения инвариантности к
полезному воздействию
, мешающие воздействия в уравнениях не учитываются:
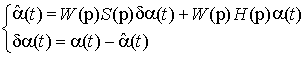(3)
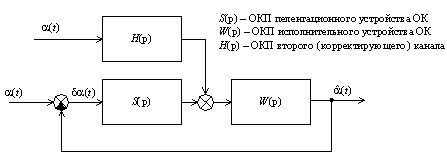
Рисунок 5 – КС
с введением дополнительной информации в кольцо слежения ОК
Из (3) получается ОКП по задающему воздействию КССЦ
.
(4)
Условие инвариантности, при котором 
воспроизводится в
системе без искажений, имеет вид
. (5)
Для достижения инвариантности следящей системы (5) ОКП 
должен быть обратным
ОКП исполнительного устройства ОК 
. ОКП исполнительного устройства представляют следующим
выражением
.
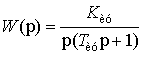Иногда ПКУ
, входящее в став ОК КИ КСС, включается в состав ИУ, тогда
.
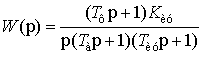ОКП связи по задающему воздействию инвариантной АИ следящей системы физически
не реализуем, так как степень полинома числителя оказывается больше степени полинома
знаменателя. Заменяя физически нереализуемый ОКП связи по задающему воздействию
близким физически реализуемым ОКП получается КИ следящая система, т. е. систему
с высокой точностью, мало отличающаяся от АИ системы. Это приводит к
определенному проигрышу в точности работы следящей системы по сравнению с АИ.
Для уменьшения этого проигрыша сигнал КК подается в контур слежения ОК
через оптимальный согласующий фильтр (СФ) с ОКП 
[3].
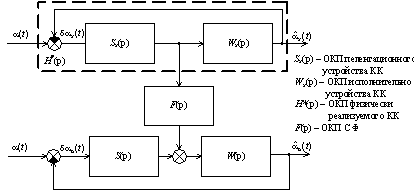
Рисунок 6 – Структурная
схема математической модели КИ КСС (с заданой структурой корректирующего канала
В общем случае динамика системы (рисунок 6), без учета мешающих
воздействий (возмущений, помех) описывается следующей системой уравнений:
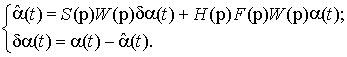(7)
Подставляя второе уравнение системы (7) в (1), получается:
,
откуда ОКП КСС в замкнутом состоянии 
, т. е. по оценке 
, равен
. (8)
Поскольку ОКП любой следящей системы по ошибке и по оценке (по задающему
воздействию) связаны простым соотношением:
, то с учетом выражения (8) получается ОКП КСС по ошибке:
. (9)
Представляя ОКП всех функциональных устройств КССЦ в виде отношения следующих
полиномов (многочленов) [3]:
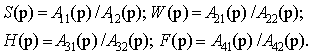(10)
в выражение (9) получается
=
.
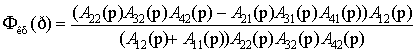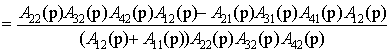(11)
Так как решается задачи синтеза КИ КССЦ при заданных структурах и
параметрах ОК и КК (т. е. когда оптимизируются только параметры СФ между
каналами), то с учетом переобозначений полиномов, определяющих функциональные
устройства КССЦ с фиксированными параметрами:
; (12)
,
выражение (11) примет вид
.
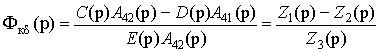(13)
Все составляющие числителя и знаменателя выражения (13) представляются в
виде
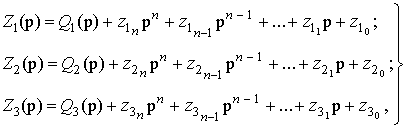(14)
где 
, 
,
– части полиномов со степенью, большей n, а соответствующие коэффициенты
полиномов вычисляются по формулам
, 
, 
.
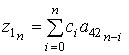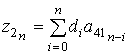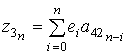(15)
Обеспечивая в (13) путем оптимизации параметров СФ (которые содержатся в
полиномах 
и 
) равенство нулю числителя, получается абсолютно инвариантная
система, которая физически нереализуема.
Для повышения порядка астатизма КИ КСС до n-го порядка повышения точности
следящей системы) обеспечивается выполнение условия равенства между собой
соответствующих коэффициентов полиномов 
, 
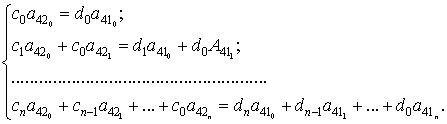(16)
Из выражения (16) следует, что конкретная величина, на которую в КИ КССЦ
может быть повышен порядок астатизма следящей системы, непосредственно зависит
от порядка полиномов числителя и знаменателя физически реализуемого оптимального
СФ между ОК и КК (см. рисунок 6).
Так как система (16) имеет в левой и правой частях неизвестные в виде
коэффициентов полиномов 
и 
, то ее решение в явном виде отсутствует. Для получения оптимального
решения системы (16), задаются конкретными значениями коэффициентов одного из
полиномов (либо
, либо
).
Подставляя в систему (16) конкретные значения коэффициентов известного полинома
, получается новая система вида
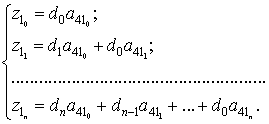(17)
Решение системы (17) представляется в векторно-матричном виде:
,
(18)
где
, 
, 
.
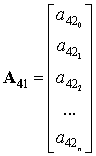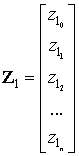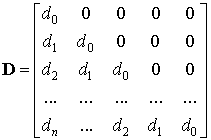Получая оптимальные параметры СФ, достигается компенсация требуемого
числа составляющих динамической ошибки следящей системы, а значит, снижается
зависимость динамической ошибки от задающего воздействия, система становится
квазиинвариантной.
Таким образом, предлагаемое теоретическое обоснование позволяет решить
задачу построения активно-пассивной квазиинвариантной комплексированной системы
сопровождения с локационными каналами (следящими координаторами цели) различных
типов, способной с высокой точностью сопровождать воздушные объекты.
Литература
1. Зайцев Г. Ф.
Теория инвариантности и комбинированное управление в автоматических системах.
Киев, КВИРТУ, 1961. 62 с.
2. Первачев С. В.
Радиоавтоматика. М., Радио и связь, 1982. 296 с.
3.
Авласенок А. В. Спец. тема: Дис. ... канд. техн. наук.
Смоленск. ВА ПВО СВ РФ, 1994. 226 с.
TRACKING
COMPLEXED SYSTEM REQUIRED ASTATICISM DEGREE ACHIEVEMENT POSSIBILITY THEORETICAL
JUSTIFICATION
Savitsky F. L., Vasilchenko
O. V.
Air objects tracking complexed system
required astaticism degree achievement possibility due to tracking dynamic
error compensation when structuring optimal complexing radar channels theoretical
justification is given in research.
Key words: complexed follow-up system, high speed low-sized air objects,
tracking precision, degree of astaticism.
Военная академия войсковой
ПВО
Вооруженных Сил Российской
Федерации
имени Маршала Советского Союза А.М. Василевского
(ВА ВПВО ВС РФ)
Поступила в редакцию 12.09.2012.