Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 12. -
Вып. 1. - 2013. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/TITL-37.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/cont.htm
УДК
623.465
АНАЛИЗ ДИНАМИКИ
САМОНАВЕДЕНИЯ ЗУР
Ó 2013 г. Царьков М. Е.
В данной работе для анализа динамики самонаведения
ЗУР, применён аналитический метод с использованием модели контура наведения с
учётом инерционных свойств. В результате анализа выявлена зависимость конечного промаха самонаводящейся ЗУР от
времени начала манёвра цели.
Ключевые слова: анализ динамики
самонаведения ЗУР.
Для анализа аналитическим методом необходимо использовать модель контура наведения с учётом инерционных свойств, обусловленных запаздыванием в образовании управляющих сил ракетой и реакцией элементов бортовой аппаратуры управления полётом ЗУР (рисунок 1).
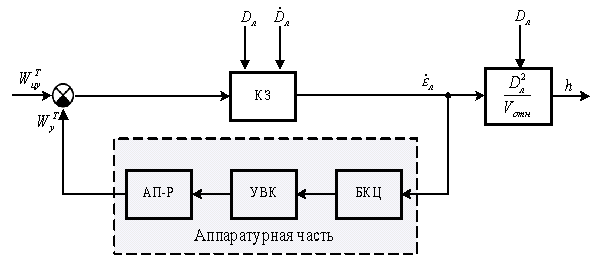
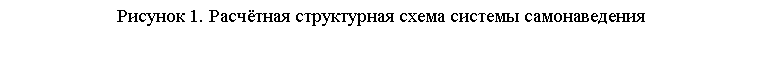
Аналитический метод исследования динамики самонаведения позволяет получать точное решение упрощенной системы дифференциальных уравнений с аппроксимацией аппаратурной части (рисунок 1) передаточной функцией вида
.
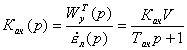(1)
Система дифференциальных уравнений, описывающая динамику движения ракеты, в рассматриваемом случае запишется следующим образом:
(2)
Система уравнений (2) введением переменной
(3)
(при допущении 
) приводится к одному уравнению замкнутой системы [1]
. (4)
Обозначив
;
,
можно получить уравнение (4) в виде
, (5)
которое является вырожденным гипергеометрическим
уравнением.
Решение неоднородного уравнения (5) можно представить через вырожденные гипергеометрические функции или специальные функции через полиномы Лягерра [1]
, (6)
где 
–
табулированная функция [1].
Для оценки качества систем
самонаведения необходимо также знать характер изменения нормального ускорения
ракеты 
с целью оценки
возможности управления ракетой при ограниченной величине располагаемых
нормальных ускорений, особенно при перехвате маневрирующих целей. Выражение для
имеет вид [1]
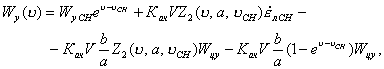(7)
где 
–
табулированная функция [1]
Таким образом, имея
зависимости угловой скорости 
и нормального
ускорения 
, представляется возможным произвести качественный и приближённый
количественный анализ динамики самонаведения.
Для оценки динамического
промаха ракеты можно воспользоваться выражением [1]
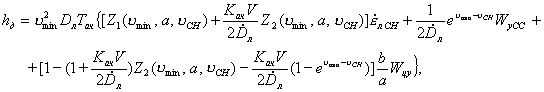(8)
|
где |
|
= |
|
|
|
|
– |
относительная дальность,
при которой прекращаетсясамонаведение. |
Из выражения (8) следует,
что величина динамического промаха ракеты зависит от параметров движения ракеты
в момент начала самонаведения, в частности, 
, от начальной угловой скорости 
, качество которых определяется качеством ПИН, а также
от характера движения цели (
) и параметров системы управления 
. В качестве примера на рисунке 2 приведены зависимости
промаха 
от начала
манёвра цели 
при различных
дальностях самонаведения и инерционных свойств контура наведения.
Как видно из рисунка 2, при
манёвре цели с увеличением величины нормального ускорения 
возрастает
величина динамического промаха. Характер увеличения 
различен при
различном времени начала манёвра и зависит от инерционности контура наведения.
Уменьшение инерционности контура наведения 
снижает
величину промаха и уменьшает 
, при котором промах достигает максимума. Как следует
из рисунка 2, манёвр цели будет эффективным с максимальным ускорением 
, если он начнётся, например, за 1-6 с до точки
встречи.
Литература
1.
Петров
Л. М. Динамика самонаводящихся ЗУР. Учебное пособие. Киев: КВАИУ им. С. М.
Кирова, 1973, 125 с.
THE ANALYSIS OF
DYNAMICS OF HOMING AGM
Tsarkov
M. Е.
In the given work the analytical method is applied
to the analysis of dynamics of homing AGM with use of model of a contour of
prompting with the account of inertial properties. As a result of the analysis
dependence of a final miss self-directed AGM from time of the beginning of maneuver
of the purpose is revealed.
Key
words: analysis of dynamics
of homing AGM.
Академия
войсковой ПВО Вооруженных Сил РФ
им.
Маршала Советского Союза А.М. Василевского,
г. Смоленск
Поступила в редакцию 29.01.2013.