Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 12. -

Вып. 1. - 2013. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/TITL-37.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/cont.htm

УДК 623.76

МОДЕЛИРОВАНИЕ ТРАЕКТОРИИ ДВИЖЕНИЯ МАНЕВРИРУЮЩЕЙ ЦЕЛИ В СРЕДЕ MATLAB

Ó 2013 г. Воробьев К. А., Сенчурин Я. Ю.

(vorobyov.doc)

Целью работы является моделирование различных видов маневров, выполняемых самолетом тактической авиации с разными скоростями и интенсивностью, для формирования входного задающего воздействия для системы управления полетом ЗУР. Конкретной задачей в рамках проблемы, на решение которой направлена работа, является оценка характеристик современных самолетов, разработка математических моделей движения целей по траекториям типовых маневров и разработка имитационной модели, позволяющей наглядно продемонстрировать движение цели, выполняющей маневр уклонения.

Ключевые слова: моделирование маневров, система управления полетом ЗУР.

В настоящее время редко встретишь труды, где бы достаточно полно описывались маневры средств воздушного нападения и техника их выполнения. Наряду с этим, в свете динамичного развития тактической авиации, большое внимание уделяется совершенствованию маневренных возможностей многофункциональных самолетов, в частности, оснащение их двигателями с отклоняемым вектором тяги и придания им новых аэродинамических схем. Следовательно, при оценке возможностей воздушной цели необходимо учитывать их высокую скорость и значительное улучшение маневренных свойств, необходимых для ведения воздушного боя и уклонения от ракетных атак как с воздуха, так и с земли.

Зачастую при изучении процесса наведения ЗУР на цель движение последней задается прямолинейно либо с небольшими отклонениями. Следовательно, проведение исследований, учитывающих перспективу развития средств воздушного нападения и способы противодействия стрельбе ЗУР, а также возможности по совершению манёвров уклонения, является актуальной задачей.

Характерной особенностью современных программ развития и модернизации авиационной техники до 2025 года является их нацеленность на создание боевого самолета пятого поколения с высокими тактико-техническими и маневренными характеристиками. Самолет пятого поколения будет иметь силовую установку, обеспечивающую крейсерский сверхзвуковой полет в бесфорсажном режиме, будут приняты серьезные меры по улучшению взлетно-посадочных и транспортных характеристик, обеспечению свойств сверхманевренности.

В тактическом плане сверхманевренность позволяет существенно повысить собственную безопасность за счет выполнения существенно более эффективных маневров уклонения от управляемых средств поражения. В техническом плане сверхманевренность требует расширения состава оцениваемых координат в пространстве и предъявляет существенно более жесткие требования к точности, быстродействию и устойчивости их сопровождения бортовыми следящими системами.

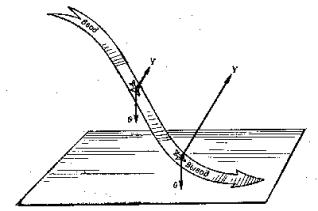
Сверхманевренность дает возможность летательному аппарату практически скачкообразно изменять свое положение в пространстве без изменения ориентации строительных осей (рисунок 1).

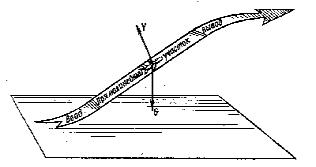
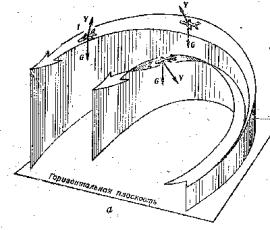
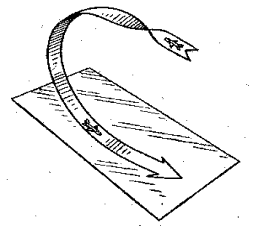
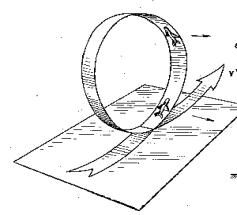
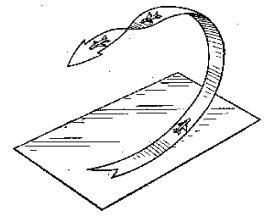
Совокупность элементарных составляющих, показанных на рисунке 1, дает возможность реализовать большее число маневров с очень сложными пространственными эволюциями. Целенаправленное выполнение манёвра, при котором появляется третья и более высокие производные дальности, скорости и угловых координат, приводящие к срыву сопровождения. Выполнение таких манёвров существенно расширяет возможности уклонения от управляемых средств поражения. К манёврам уклонения можно отнести: вираж; пикирование (с углами наклона до 60°); горка (с углами наклона до 60°); боевой разворот; штопор, переворот; мёртвая петля; переворот Иммельмана и др. (рисунки 2 – 7).

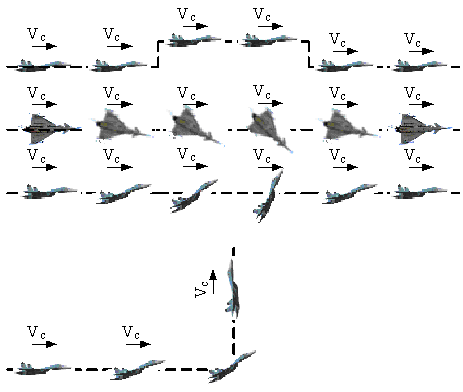
Рисунок 1 − Элементарные составляющие сверхманёвренности летательных аппаратов

Известно, что математическое моделирование – это область науки и техники, которая обеспечивает выявление закономерностей протекания различных явлений окружающего нас мира или работы систем и устройств путем их математического описания и моделирования без проведения натурных испытаний. При этом используются фундаментальные положения и законы математики, описывающие моделируемые явления, системы или устройства на некотором уровне их идеализации.

Различают аналитические и имитационные математические модели. При аналитическом моделировании все случайные величины заменяются их числовыми характеристиками, и устанавливается однозначная связь между исходными данными и результатами. В имитационных моделях действие случайного фактора имитируется при помощи датчика случайных чисел, и поэтому на выходе получаются различные результаты даже при одних и тех же исходных данных, которые затем обрабатываются. Такие модели точнее описывают реальный процесс, но требуют применения ЭВМ с соответствующим быстродействием.

Выбор формализованной модели движения цели основывается на анализе способов противодействия СВН наведению зенитных ракет. Следует отметить, что эффективность маневров уклонения базируется на особенностях систем наведения ЗУР: на инерционности самих ракет, их систем управления и на специфике обработки сигналов. В соответствии с первой особенностью всегда имеет место запаздывание реакции ракеты на маневр цели. Известно, что использование факта запаздывания реакции ракеты особенно эффективно, если интенсивный маневр уклонения выполняется за 1–2 с до подлета ракеты к дальности срыва наведения r_лк за счет потери управления, обусловленного ограниченными возможностями систем отслеживания или «ослепления» ГСН. Однако следует подчеркнуть, что в современных ЗР с полуактивными и активными РГСН, пассивными оптическими ГСН величины относительной дальности срыва наведения r_лк незначительны. Кроме того, современные ЗР обладают очень большим диапазоном располагаемых перегрузок, позволяющим реагировать на маневр цели с очень малым запаздыванием.

Рисунок 2 – Манёвр «пикирование»	Рисунок 3 – Манёвр «горка»
Рисунок 4 – Манёвр «боевой разворот»	Рисунок 5 – Манёвр «переворот»
Рисунок 6 – Манёвр «петля Нестерова»	Рисунок 7 – Манёвр «переворот Иммельмана»

Более предпочтительным является использование второй особенности, позволяющей совершать эффективный маневр уклонения на любом расстоянии до ракеты. Это направление основано на целенаправленном выполнении самолетом таких маневров, при которых либо нарушаются условия его обнаружения в ГСН, либо возникают производные отслеживаемых дальностей, скоростей и углов с порядком, превышающим порядок астатизма следящих измерителей ИВС ракеты. Поскольку в части существующих на вооружении ЗР используются измерители с астатизмом, не превышающим второй порядок, то достаточно выполнить интенсивный маневр, в процессе выполнения которого появляются производные дальности, скорости и бортовых пеленгов третьего порядка. При выполнении таких маневров в следящих измерителях с астатизмом второго порядка возникают нарастающие во времени динамические ошибки. При ограниченной ширине рабочих участков дискриминационных (пеленгационных) характеристик нарастание динамических ошибок, в конечном счете, приводит к срыву наведения ракеты.

Одной из разновидностью маневров уклонения является обеспечение полета самолета по такой траектории, при которой конечный промах h_к превышает заданное значение h_зад, определяемое эффективным радиусом R_эф достоверного срабатывания неконтактного датчика цели боевого снаряжения ракеты, т. е. h_к > h_зад ≥ R_эф.

Заданную величину промаха h_зад можно определить из формулы вероятности попадания ракеты в трубку допустимого промаха h_доп = R_эф

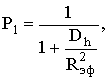(1)

где D_h – дисперсия промаха.

Определяя из выражения (1) D_h, можно получить

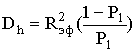
или

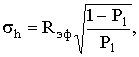(2)

где σ_h – СКО промаха h.

При гауссовском законе распределения промахов обычно полагают

h_зад = 3σ_{h зад}.

Например, при Р₁ ≤ 0,3 величина σ_{h зад} согласно (2) равна

σ_{h зад} ≥ 1,53R_эф

или

h_зад ≥ 4,6R_эф.

При этом учитывалось, что задача уклонения решалась в предположении наведения ЗР на цель по методу пропорционального сближения, широко применимому в самонаводящихся зенитных ракетах.

На рисунке 8 приведен фрагмент операционной модели в компьютерной среде MATLAB, которая формирует задающее воздействие в виде маневра для контура самонаведения.

Закон изменения требуемого нормального ускорения цели для осуществления маневра в вертикальной плоскости определяется в виде

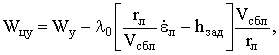(3)

где λ₀ – любое положительное число, выбираемое с учетом прогнозируемого метода наведения атакующей ракеты.

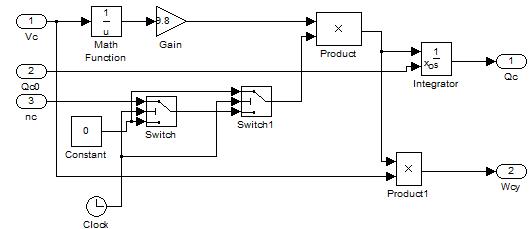
Рисунок 8 – Модель формирования маневра цели

Закон изменения требуемого нормального ускорения цели для осуществления маневра в вертикальной плоскости определяется в виде

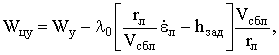(3)

где λ₀ – любое положительное число, выбираемое с учетом прогнозируемого метода наведения атакующей ракеты.

Например, с учетом метода пропорционального сближения и выборе выражение (3) примет вид

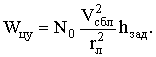(4)

При определении выражения (3) были учтены допущения о том, что и цель движется по линии близкой к линии визирования «ракета–цель».

Из выражений (3), (4) следует, что чем больше заданное значение промаха h_зад, тем больше потребное значение нормального ускорения цели, необходимого для осуществления маневра данным способом уклонения. Как видно из выражения (3), если текущий промах 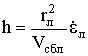равен значению h_зад, то нормальное ускорение цели равно текущему нормальному ускорению ракеты. Следует также заметить, что если располагаемые нормальные ускорения зенитных ракет в несколько раз превышают предельно допустимые нормальные ускорения цели, то задача обеспечения любого произвольно заданного значения промаха h_зад является трудно разрешимой. Из выражений (3) и (4) видно также, что чем меньше относительная скорость сближения V_сбл, тем меньше потребное нормальное ускорение цели, необходимое для обеспечения заданного промаха h_зад. Очевидно, что в данном случае наиболее эффективен маневр уклонения будет достигаться при атаке ракетой цели на догонном курсе. При этом, если скорость полета цели на момент атаки ракетой не является максимальной, то за счет ее увеличения можно существенно снизить скорость сближения. Уменьшение V_сбл позволяет значительно снизить требования к потребным значениям нормального ускорения цели.

Существенно можно повысить эффект маневра уклонения путем комбинации данного способа с маневром «змейка». Такой способ получил название «набегающей» или «убегающей» змейки в зависимости от направления атаки ракеты, а именно при атаке навстречу или вдогон. В этом случае закон изменения нормального ускорения цели, например, для реализации уклонения от ракеты наводящейся по методу пропорционального сближения можно представить в виде

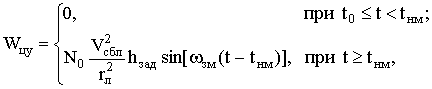(5)

где t₀ – время пуска ракеты;

t_нм – время начала маневра цели;

ω_зм – частота колебаний.

Модель (5) позволяет изменением величины ω_зм имитировать также такие виды маневров как колокол, пикирование с выходом из него и др. На рисунке 2.2 приведен фрагмент операционных моделей типовых маневров воздушной цели с ручным переключением.

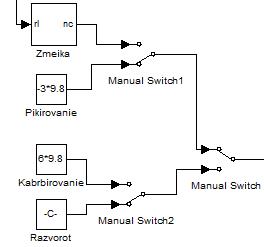
Рисунок 9 – Реализация ручного переключения типовых маневров воздушной цели

Исследование процесса наведения ЗУР на цель методом моделирования позволяет оценить потенциальное качество наведения и эффективность перехвата целей с помощью показателей устойчивости и точности без проведения полигонных испытаний.

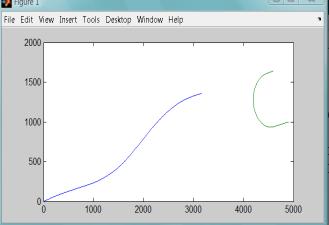
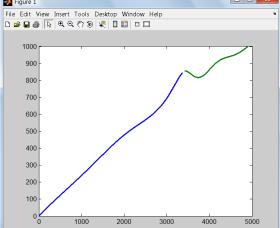
Известно, что математическое моделирование при изучении сложных динамических систем наведения позволяет оценить потенциальное качество наведения и эффективность перехвата целей с помощью показателей устойчивости и точности. В имитационной модели процесса наведения ЗУР на цель формируются алгоритмы, обеспечивающие наглядное представление о траекториях полета цели и ракеты. На рисунках 10–13 приведены примеры наведения ЗУР на цель, совершающей различные маневры.

Моделирование процесса наведения ЗУР БД на маневрирующую цель проводилось при следующих исходных данных.

1. Имитировался полет цели на высоте H_ц=1000–1500 м, летящей со скоростью V_ц=150–310 м/с при курсовом параметре Р_ц=300–1200 м.

2. Имитировалось наведение ЗУР на цель совершающую маневр после пуска ЗУР с постоянной перегрузкой n_ц=2–6 ед. в вертикальной плоскости.

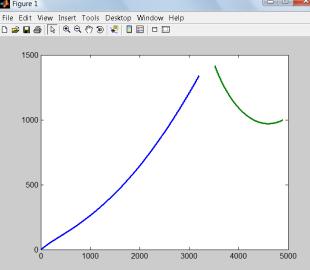
Рисунок 10 – Реализация маневра «иммельман»	Рисунок 11 – Реализация маневра «набегающая змейка»
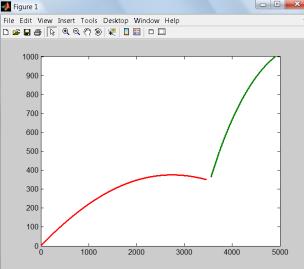
Рисунок 12 – Реализация маневра «пикирование»	Рисунок 13 – Реализация маневра «кабрирование»

Научная новизна и теоретическая значимость работы обуславливаются следующими новыми научными результатами, полученными в ходе исследований:

· проведена оценка потенциальных возможностей современных самолетов тактической авиации иностранных государств;

· проведен анализ способов совершения противозенитных маневров средствами воздушного нападения;

· разработана математическая модель маневрирующей цели в компьютерной среде MATLAB.

Литература

1. Володин В. Что стоит во главе угла отношения к сверхманевренности самолета // «Независимое военное обозрение», № 1, 2009. 2. Якушенков Ю.Г., Тарасов В. В. Инфракрасные системы «смотрящего» типа. - М.: «Логос», 2004. 430 с.

2. Хуторской И. Н., Финогенов С. Н. Системы наведения зенитных ракет с оп-тимальным управлением. Смоленск, ВА ВПВО ВС РФ, 2008. 327 с.

3. Воробьев К. А. Системы управления ЗУР с применением нечеткого супервизорного регулирования // Автоматизация и современные технологии. № 2, 2011. С. 14−18.

4. Свидетельство об официальной регистрации программы для ЭВМ в Институте научной информации и мониторинга РАО, ОФЭРНиО № 16973. Случайный маневр/ Воробьёв К. А., Марченков Д. А., Кадученко И. В., 2011.

DESIGN OF TRAJECTORY OF MOTION MANOEUVRING PURPOSE IN ENVIRONMENT MATLAB

Vorobyov K. A., Senchurin Y. Y.

The design of different types of manoeuvres executable by air of tactical aviation with different speeds and intensity is the purpose of work, for forming of entrance questioner influence for the mission-control AGM system. By a concrete task within the framework of problem on the decision of which work is directed, there is estimation of descriptions of modern airplanes, development of mathematical models of motion of aims directionally models manoeuvres and development of simulation model, allowing evidently to show motion of purpose executing the manoeuvre of deviation.

Key words: manoeuvres executable by air of tactical aviation, mission-control AGM system

Академия войсковой ПВО Вооруженных Сил РФ

им. Маршала Советского Союза А.М. Василевского,

г. Смоленск

Поступила в редакцию 29.01.2013.