Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 12. -
Вып. 1. - 2013. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/TITL-37.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-37-html/cont.htm
УДК 358.116
Научное обоснование
структуры и параметров адаптивного фильтра оценки координат в условиях стрельбы
ЗСУ ЗПРК в движении
Ó
2013 г. Желнин А. А.
В данной работе изложен
подход к обоснованию структуры и параметров адаптивного фильтра, работающего в
условиях возмущений возникающих в при движении объекта. Предлагаемый алгоритм свободен от недостатков
присущих фильтрам Калмана, которые строятся на основе такого же метода оптимизации
коэффициентов фильтра. Алгоритм позволяет оптимизировать процесс выработки
первой и второй производных в особых условиях. В работе проведено исследование
динамической, флюктуационной и полной ошибок фильтрации при условии
устойчивости, приведена методика расчета оптимальных коэффициентов фильтра.
Ключевые слова: адаптивный
фильтр.
Вычислительный процесс по рассматриваемому алгоритму реализуется на специализированном цифровом вычислителе, решающем задачу оценки и сглаживания прямоугольных координат цели, при использовании полиноминальной модели входного воздействия.
Основу алгоритма составляют
разностные уравнения, описывающие закон изменения во времени стабилизированных
несглаженных прямоугольных координат цели X, Y, H. независимой переменной в
уравнениях является безразмерное время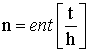 
, h – величина тактового периода ЦВС и равна 0,02 с, t –
текущее время. Для всех координат X, Y, H используется одинаковая
форма записи разностных уравнений. Корреляционные связи между уравнениями отсутствуют.
Это позволяет производить оценку динамических свойств, исследуя работу фильтра
по одной из координат, например X.
Разностные уравнения позволяющие получить измеренные
фильтром фактическое значение прямоугольной координаты 
и значения ее первых
двух производных 
, 
, имеют вид:
;
;
;
; (1)
;
;
;
где 
, 
, 
– экстраполированные
на n-ый такт вычислений значения прямоугольной координаты и её производных,
полученные по результатам измерений в 
такте;
, 
, 
– постоянные или
изменяющиеся во времени коэффициенты.
На нулевом такте вычислений
в качестве начальных условий вводятся величины 
, 
, 
. Величина 
формируется при обнаружении цели и грубом измерении её
координат в момент перехода к сопровождению цели с помощью оптического прицела
или теплопеленгатора.
Система разностных уравнений
(1) описывает процедуру фильтрации вновь поступающих данных. В процессе формирования
экстраполированных значений предполагается, что за время h
скорость изменения координаты 
и её ускорение 
сохраняют постоянные значения.
Ошибка 
формируется в каждом
такте вычислений. Она подвержена искажениям за счет шумов и флюктуаций
поступающей входной координаты 
. Наличие возмущения в виде флюктуаций координаты 
, заставляет выбирать коэффициенты 
, 
, 
меньше 1. При этом их
величина должна быть тем меньше, чем выше уровень возмущающих воздействий.
Уменьшение коэффициентов эквивалентно сужению полосы пропускания фильтрующей
системы, что приводит к ослаблению действия возмущений. Однако с уменьшением коэффициентов
, 
, 
возрастает динамическая
ошибка, так как при их значениях меньше 1 всегда будет уменьшаться величина
истинной координаты, содержащейся 
.
Анализ динамических свойств
фильтра оценки координат удобно провести с помощью Z-преобразования уравнений
входящих в систему (1), с учетом 
.
При этом система уравнений
(1) примет вид:
;
;
;
; (2)
;
;
;
Исходя из полученной системы уравнений (2) можно получить передаточные функции фильтра оценки координат:
;
;
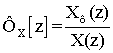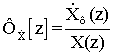(3)
.
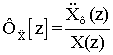Для получения передаточных функций (3) целесообразно систему (2) переписать в виде:
;
;
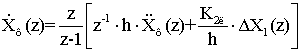; (4)
.
Исходя из системы уравнений (4) передаточные функции фильтра оценки координат будут иметь вид:
;
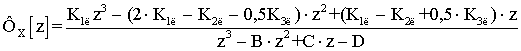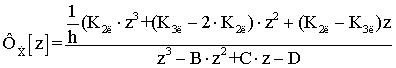; (5)
.
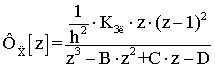где
;
Во всех передаточных функциях степень полинома числителя не превышает степень полинома знаменателя, следовательно, фильтр является физически реализуемым.
Оценка устойчивости
алгоритма проводится на основе анализа коэффициентов характеристического
полинома знаменателя передаточных функций (5), который в общем виде записывается
следующим образом
.
В рассматриваемом случае имеем полином 3-ей степени,
для которого условия устойчивости имеют вид [1]
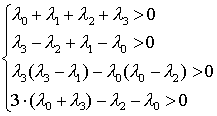(6)
где:
; 
; 
; 
,
тогда неравенства системы примут вид:
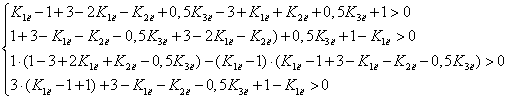
Преобразовав
систему неравенств получаем:
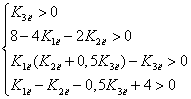(7)
Для
решения системы неравенств определим значения 
, 
, 
при которых будет выполнятся
равенство уравнений 2, 3, 4 системы (7)
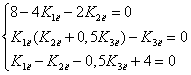(8)
Из
уравнения 1 и системы уравнений (7), получим,
,
(9)
подставим
(9) в уравнение 3 системы уравнений (7), получим
.
(10)
Подставим
(9) и (10) в уравнение 2 системы уравнений (7), получим
(11)
Из
(11) получим 
Подставим
значения 
в (9) и (10), получим
Таким образом мы определили
значения 
, 
, 
при которых выполняется
(8). Теперь определим диапазон 
, 
, 
при которых будет выполняться (7).
Очевидно 
, 
, 
не могут быть
отрицательными, следовательно, из уравнения 2 системы неравенств (7) 
, 
, причем при увеличении 
, уменьшается 
.
Из выражения 4 (7),
определим 
, причем при 
; 
.
Динамическая ошибка в работе ФОК вызывается его инерционностью. Для определения величины
ошибки рассматривается ее Z-преобразование
где: 
– соответственно
дискретная передаточная функция фильтра по ошибке и Z-преобразование входного
воздействия
Для получения числовых характеристик динамической ошибки необходимо рассматривать ее установившееся значение при некоторых типовых законах изменения входного воздействия.
Анализируемый фильтр имеет
астатизм 3-го порядка. Поэтому установившееся значение динамической ошибки
будет отлично от нуля для входных воздействий имеющих производную третьего порядка.
Пусть оцениваемая фильтром
координата изменяется по закону
,
где: 
– производная
ускорения по координате 
;
– функция Хевисайда.
Используя таблицу Z-преобразований [1, 2],
можно записать
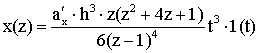
Дискретная
передаточная функция фильтра по ошибке находится из соотношения [3]
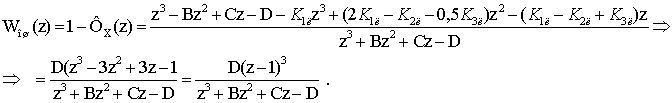
Установившееся
значение динамической ошибки 
определяется в соответствии с выражением [3]
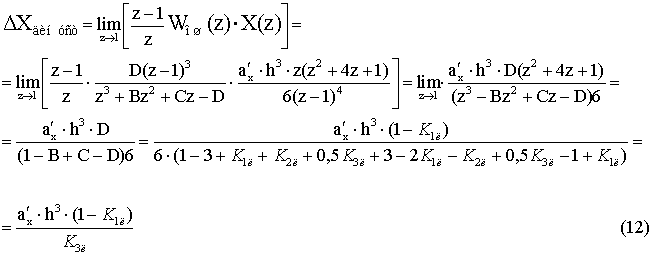
Таким образом, уменьшение
динамической ошибки в оцениваемой фильтром координате достигается увеличением коэффициента
и при 
→1, при условии 
<1.
Полученное выражение (12)
для определения динамической ошибки ФОК является необходимым условием процедуры
синтеза фильтра, обеспечивающего экстремум выбранного критерия качества измерений.
Оптимизацию параметов фильтра необходимо осуществлять минимизацией суммарной
ошибки измерений, производимых фильтром
(13)
где
– дисперсия
флюктуационной составляющей в измеренной фильтром координате.
В этом случае последовательность синтеза сводится к решению следующих задач:
1.
Оценка
динамической ошибки фильтрации 
.
2.
Расчет
дисперсии флюктуационной ошибки фильтрации 
.
3.
Определение
в общем виде выражения, характеризующего суммарную ошибку фильтрации.
4.
Нахождение
коэффициентов ФОК, обеспечивающих минимум суммарной ошибки фильтрации.
Для нахождения флюктуационной ошибки измерений
необходимо оценить реакцию фильтра на шумовой процесс, вызванный ошибками при
съеме информации о координате на датчиках ЦВС. Учитывая сверхманевренные возможности
современных СВН и интервал дискретизации h=0,02 с, можно считать, что
на входе ФОК образуется дискретный случайный процесс типа «белого шума» с
дисперсией 
.
С учетом используемого
аппарата Z – преобразования разностных уравнений фильтрации
можно по значению дискретной дисперсии 
и дискретным
передаточным функциям фильтра 
, 
, 
определить дисперсии
флюктуационных ошибок при измерении координаты 
, её скорости 
и ускорения 
.
Для дискретных
систем эти дисперсии определяются [3, 4]:
;
;
;
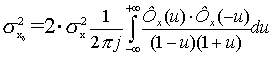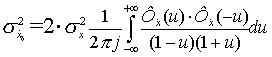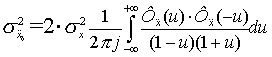где 
– переменная
билинейного преобразования соответствующей дискретной передаточной функции
замкнутого фильтра, связанная с переменной Z соотношением 
.
Необходимость
применения билинейного преобразования обусловлена периодичностью амплитудно-частотной
характеристики цифрового фильтра, что требует замены пределов интегрирования в
интеграле Парсеваля, применяемых для подобных расчетов при анализе аналоговых
систем автоматического управления.
Получаемые при
замене переменной интегралы вычисляются по табулированным формулам.
Итак рассмотрим
флюктуационную ошибку в оценке координаты 
с учетом ввода замены
переменной 
.
Проведя замену
переменной в дискретной передаточной функции 
получим
|
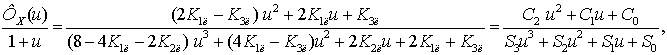
где |
|
|
|
|
; 
; 
; 
; 
; 
Проведенные преобразования позволяют
применить табличную формулу, которая применяется для вычисления интегралов типа [1]
;
|
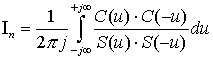где |
|
|
|
|
; 
; 
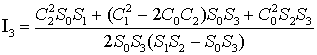
Подстановка
коэффициентов и приведение подобных позволяют получить выражения для дисперсий
ошибок измерений цифровым фильтром:
;
;
;
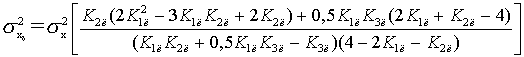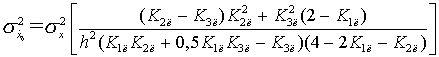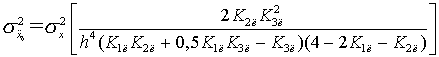Таким образом,
общая тенденция состоит в том, что для снижения флюктуационных ошибок следует
уменьшать указанные коэффициенты
, 
, 
, постоянно контролируя при этом выполнение условий устойчивости
фильтра (7).
Полученные в
подразделах 3.3 и 3.4 результаты позволяют в окончательном виде записать
выражение для суммарной дисперсии ошибок измерений фильтра оценки координат
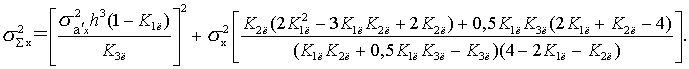
Для вычисления оптимальных коэффициентов фильтра
используется переход к относительной суммарной дисперсии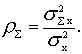 
Выражение для 
будет иметь вид:
,
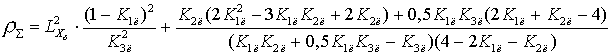где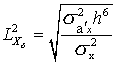
– индекс слежения, который численно характеризует соотношение
между ошибкой, выраженной поступательным движением цели относительно ЗРК, и
ошибкой вызванной флюктуациями координаты на входе цифрового фильтра.
Вычисление
оптимальных коэффициентов фильтра по критерию минимума 
сводится к численному
решению системы уравнений:
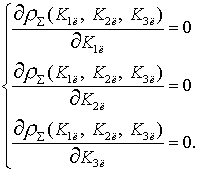
Полученные в
результате такого решения коэффициенты будут оптимальны, так как обеспечивают
минимум дисперсии 
ошибки измерений, а
вычисление этих значений можно производить в ЦВС в реальном масштабе времени
или хранить их в ПЗУ ЦВС для конкретных характеристик 
, 
, 
. Последние получают в ходе экспериментальных натурных исследований
для различных видов движений воздушной цели относительно ЗРК.
Применительно к
задаче, решаемой в диссертации получено, что оптимальные коэффициенты ФОК
должны удовлетворять следующей системе уравнений:
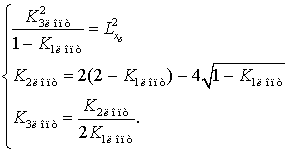
Результаты численного решения такой
системы уравнений позволяют выбрать оптимальные значения коэффициентов для
конкретных условий ведения огня ЗСУ 2С6М1 с ходу.
При этом погрешности работы фильтра
оценки координат можно охарактеризовать матрицей дисперсий
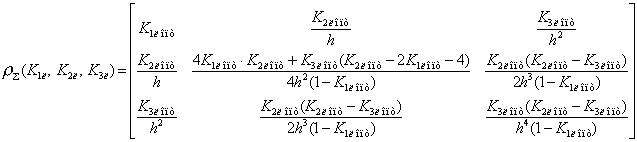
Диагональные
элементы этой матрицы характеризуют дисперсию ошибок измерения координаты, ее
первой и второй производной. Остальные элементы матрицы характеризуют корреляционные
моменты взаимной связи.
Таким образом
для заданного значения 
, характеризующего маневр цели и действующего на входе
фильтра возмущения, можно в ЦВС определить оптимальные коэффициенты 
, 
, 
. Затем используя матрицу дисперсий 
, возможно рассчитывать средние квадратические ошибки
измерений компенсируя их путем вариации коэффициентов фильтра.
Наиболее просто
организовать определение оптимальных коэффициентов фильтра на основании
конечного числа последних полученных отсчетов, вырезаемых скользящим окном.
Кроме этого можно вводить убывание веса отсчета с удалением его от текущего момента
времени, можно управлять количеством накопленных отсчетов, по которым рассчитывается
измеряемая координата. При этом концепция индекса слежения 
обеспечивает оптимизацию
параметров фильтра для данной неопределенности относительного движения цели и
ЗСУ, а также неопределенности в возможностях измерения параметров движения
воздушной цели.
Применяемый
цифровой фильтр свободен от недостатков
присущих фильтрам Калмана, которые строятся на основе такого же метода
оптимизации коэффициентов фильтра. Однако фильтрам Калмана присущ существенный
недостаток – с течением времени алгоритм калмановской фильтрации становится не
чувствительным к вновь получаемым измерениям. Метод борьбы с таким недостатком
заключается в применении экспоненциального убывания веса прошлого измерения
(экспоненциальное забывание) по мере удаления его от текущего момента
измерения. Однако корректное применение этого метода связано с необходимостью
численного решения дифференциального уравнения Рикатти, что не всегда возможно,
а зачастую получаемое решение приводит к расходимости фильтра, особенно если
движение воздушной цели отличается от принимаемой для решения гипотезы.
Литература
1. Трахтман А. М., Трахтман В. А. Основы
теории дискретных сигналов на конечных интервалах. М., «Сов. радио», 1975, 208
с.
2. Лайонс Р. Цифровая обработка
сигналов. М., Бином-Пресс, 2006. - 653 с.
3. Белодедов М.
В. Методы проектирования цифровых фильтров. - Волгоград.: Изд-во ВолГУ, 2004. 64 с.
4. Сергиенко А.
Б. Цифровая обработка сигналов: Учебник для вузов. - СПб.: Питер, 2002. - 608
с.
SCIENTIFIC
JUSTIFICATION OF STRUCTURE AND PARAMETERS OF THE ADAPTIVE FILTER OF AN
ASSESSMENT OF COORDINATES IN THE CONDITIONS OF ZSU ZPRK FIRING IN MOVEMENT
Zhelnin A. A.
In this work the approach to justification of
structure and parameters of the adaptive filter working in the conditions of
indignations of arising in at movement of object is stated. The offered
algorithm is free from shortcomings inherent in Kalman's filters which are
under construction on the basis of the same method of optimization of factors
of the filter. The algorithm allows to optimize process of development of the
first and second derivatives in special conditions. In work research of
dynamic, flyuktuatsionny and full errors of a filtration under condition of
stability is carried out, the design procedure of optimum factors of the filter
is given.
Key words: adaptive filter.
Автор:
Желнин Алексей Аркадьевич, 1976 г. р.,
преподаватель кафедры Военной академии войсковой ПВО Вооруженных Сил РФ им.
Маршала Советского Союза А. М. Василевского, г. Смоленск.
Область научных интересов:
системы стабилизации координаторов и
оптимальная обработка сигналов.
Раздел журнала: «Радиотехника»
Рабочий телефон: (4812) 29-98-37
Домашний телефон: +79107694452
E-mail: zelnin76@mail..ru
Академия
войсковой ПВО Вооруженных Сил РФ
им. Маршала
Советского Союза А.М. Василевского, г. Смоленск
Поступила в
редакцию 21.02.2013.