Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 12. -
Вып. 2. - 2013. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-38-html/TITL-38.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-38-html/cont.htm
УДК 004.021
КЛАСТЕРНЫЙ ГЕНЕТИЧЕСКИЙ АЛГОРИТМ ДЛЯ ПОСТРОЕНИЯ МНОЖЕСТВА ПАРЕТО В
ЗАДАЧЕ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Ó 2013 г. Макушин Д. А.
Все большее распространение повсеместно получают
различные стохастические и эволюционные алгоритмы. Одним из таких алгоритмов
является кластерный генетический алгоритм, который, как и стандартный
генетический алгоритм, основывается на эволюционных принципах, но в тоже время
позволяет поддерживать до последнего шага своей работы разнообразие популяции,
благодаря разбиению пространства поиска.Рассматривается применение этого метода
для приближенного построения множества Парето в задаче многокритериальной
оптимизации.
Ключевые
слова. Многокритериальная задача,
кластерный генетический алгоритм, множество Парето, эволюционные алгоритмы.
Постановка
задачи. Совокупность частных
критериев оптимальности 
образует векторный
критерий оптимальности 
, где 
– вектор варьируемых
параметров. Ставится задача минимизации каждого из частичных критериев в одной
и той же области допустимых значений вектора варьируемых параметров 
. Запишем задачу многокритериальной оптимизации в виде
. (1)
Положим, что частные критерии оптимальности тем или
иным образом нормализованы.
Векторный критерий оптимальности 
выполняет отображение множества 
в некоторую область 
, где 
- пространство
критериев. Будем говорить, что вектор 
предпочтительнее
вектора 
, и писать 
, если среди равенств и неравенств 
имеется хотя бы одно
строгое неравенство. Аналогично, будем говорить, что векторный критерий
оптимальности 
доминирует векторный
критерий оптимальности 
, и писать 
, если 
.
Во множестве 
выделим подмножество 
точек, для которых в
этом подмножестве нет точек, их доминирующих. Подмножество 
называется фронтом Парето,
а подмножество 
, соответствующее множеству 
– множеством Парето (переговорным множеством, областью
компромисса).
Ставится задача приближенного построения множества
Парето (а тем самым, и фронта Парето) в задаче многокритериальной оптимизации
(1) [2].
Метод
многокритериальной оптимизации с использование кластерного генетического
алгоритма. Особенностью кластерного
генетического алгоритма (КГА) является наличие совершенно особенной
подпопуляции, содержащей кластеры хромосом, которые формируются по принципу
фенотипического отличия друг от друга. Эта подпопуляция позволяет поддерживать
разнообразие основной популяции, необходимое для параллельного исследования
всех областей пространства поиска.
Каждый кластер – это набор решений, которые обладают
схожими свойствами (в данном случае, кодируемых хромосомами с похожими
фенотипами).
Для определения меры близости в данном случае
используется бинарная (Хемминга) метрика 
. Число кластеров зависит от параметров области поиска и
задаваемого радиуса гиперсферы кластера 
. Если хромосом располагается в пределах 
до центроида кластера
, то он считается принадлежащим 
. Кластеризация элементов популяции производится по принципу
доминирования.
Пусть 
фрагментов популяции 
, представляющих собой кластеры. Хромосома 
является доминирующей
в кластере, если для 
(здесь
предполагается, что решается задача минимизации). Знак нестрого неравенства означает,
что в кластере может быть более одного доминирующего решения. Поэтому хромосома
является центроидом
кластера 
тогда и только тогда,
если для 
. Важно, что отдельные хромосомы, соответствующие этому
неравенству, могут принадлежать одновременно и другим кластерам, а также доминировать
сразу в нескольких кластерах [1].
Для обработки подпопуляции найденных центроидов
вводятся две дополнительные вычислительные процедуры – выделения и копирования
кластеров (рис.1).
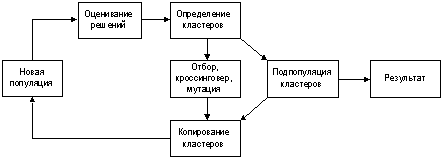
Рис. 1. Структура кластерной модификации генетического
алгоритма (ГА)
Процедура выделения кластеров состоит в определении 
кластеров,
определяемых координатами центроидов. Под центроидом понимается хромосома,
доминирующая все другие хромосомы принадлежащие к данному кластеру, находящиеся
на расстоянии не превышающем 
от нее.
Центроиды кластеров сохраняются в отдельной
подпопуляции. После этого основная популяция подвергается применению
генетических операторов и претерпевает изменения, найденные кластеры теряются.
Затем, для восстановления «присутствия» ГА в соответствующих участках
поискового пространства, сохраненные центроиды копируются в основную популяцию.
Происходит это следующим образом: «худшая» хромосома
из некоторого кластера заменяется своим центроидом. Если такая хромосома
отсутствует, то на центроид заменяется «худшая» хромосома новой популяции, не
принадлежащая ни одному из кластеров.
Так как в данном случае речь идет о многокритериальной
задаче, соответствующие необходимые изменения претерпел генетический оператор
отбора. Сравнение хромосом должно проводиться с использованием векторного
критерия оптимальности. Кроме того, при решении многокритериальной задачи
глобально лучшие решения отыскиваются на множестве Парето. С этой целью
выполнено преобразование этапа оценки решений, полученных в ходе работы
алгоритма. Таким образом, на этапе формирования новой популяции хромосом 
с множеством генов 
и множеством частных
критериев оптимальности 
, в нее попадают лишь те хромосомы, которые удовлетворяют
условию, что 
.
Реализация. Для того чтобы иметь возможность точной оценки аппроксимации, исследование
эффективности выполнено для простой двумерной задачи с известным решением:
·
множество допустимых
значений вектора варьируемых параметров
(2)
·
частные критерии
оптимальности
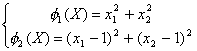(3)
Для КГА использованы следующие параметры: размер
популяции 
; вероятность скрещивания 
; вероятность мутации 
; Радиус гиперсферы кластера 
; количество эпох 
.
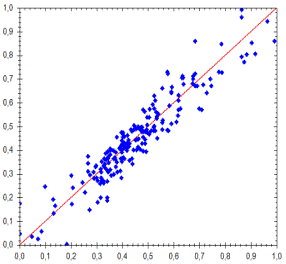
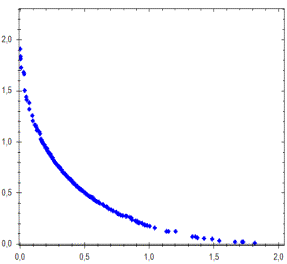
Эффективность метода с учетом указанных условий иллюстрирует
рисунок 2. Точные решения этой задач представляют собой отрезок прямой с
координатами (0,0) и (1,1); Точный фронт Парето – дуга окружности проходящая
через точки (0,2), (2,0), (0,5,0,5). Средняя ошибка аппроксимации на
завершающем этапе работы алгоритма
.
|
|
|
|
а) |
б) |
|
Рис. 2. Аппроксимация множества Парето (а) и фронта Парето (б) |
|
Для дальнейшего улучшения работы алгоритма необходима
дополнительная проработка механизма сравнения хромосом и возможное усиление векторного
критерия оптимальности дополнительными условиями. Например, минимизацией суммарной
оценки частных критериев.
ЛИТЕРАТУРА
1. Казаков П. В. Кластерный генетический алгоритм
синтеза оптимальных решений задачи инвестирования. – Брянский государственный
технический университет, 2004. - 5 с.
2. Антух А.Э., Карпенко А.П., Семенихин А.С.
Исследование эффективности архитектуры CUDA для аппроксимации множества Парето
с помощью метода роя частиц. – Вестник ЮУрГУ №37(254), 2011 – С. 63–70.
CLUSTER
GENETIC ALGORITM FOR THE APPROXIMATE THE PARETO SET FOR MULTI-CRITERIA
OPTIMIZATION PROBLEM
Makushin D. A.
Becoming more
common all over the place and getting different stochastic evolutionary algorithms.
One of these algorithms is the cluster genetic algorithm, which is a standard
genetic algorithm, based on evolutionary principles, but at the same time
allows you to maintain to the last step of his diversity of the population, due
to the decomposition of the search space. The application of this method for
the approximate Pareto set for multi-objective optimization problem.
Keywords. Multi-criteria problem, cluster genetic
algorithm, Pareto set, evolutionary algorithms.
Филиал федерального государственного
бюджетного образовательного
учреждения высшего профессионального
образования
«Национальный исследовательский университет
«МЭИ»
в г. Смоленске
ssnakevp@gmail.com
Поступила в редакцию
29.05.2013.