Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 12. -
Вып. 2. - 2013. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-38-html/TITL-38.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-38-html/cont.htm
УДК
623.4
МЕТОДИКА СИНТЕЗА КВАЗИИНВАРИАНТНОЙ КОМПЛЕКСИРОВАННОЙ СИСТЕМЫ СОПРОВОЖДЕНИЯ ВОЗДУШНЫХ ОБЪЕКТОВ
Ó 2013 г.
Савицкий Ф. Л., Васильченко О. В., Муравский А. П.
В работе представлена методика синтеза комплексированной системы автоматического
сопровождения воздушных объектов, у которой достигается требуемый порядок
астатизма за счет организации оптимальной связи между комплексируемыми локационными
каналами.
Ключевые слова: методика, комплексирование,
высокоскоростные малоразмерные воздушные объекты, точность сопровождения,
порядок астатизма.
Непрерывное увеличение числа малоразмерных летательных аппаратов, которые все больше используются в частных интересах, ведет к росту угрозы национальной безопасности (использование их в целях совершения террористического акта). В связи с этим возникает необходимость эффективно реагировать на такие угрозы.
В настоящее время существует система контроля воздушного пространства, которая позволяет вскрывать факт угрозы, но не ликвидировать ее. Для уничтожения малоразмерных маневренных летательных аппаратов, которые создают угрозу национальной безопасности, целесообразно применять средства противовоздушной обороны. Между тем, сравнительно не большая эффективная площадь рассеяния этих летательных аппаратов и высокая их маневренность стали основными факторами, затрудняющими их уничтожение.
Влияние данных факторов особенно актуально для систем автоматического сопровождения воздушных объектов (ВО) по направлению средств ПВО, проявляющееся в росте ошибки сопровождения, вплоть до его срыва.
Таким образом,
задача повышения точности сопровождения является актуальной в интересах
повышения национальной безопасности.
Как известно, для достижения
заданной точности автоматического сопровождения, как правило, используются оптимальные
(синтезированные при фиксированных характеристиках процесса) следящие системы.
Однако современным следящим системам
приходится функционировать в условиях априорной неопределенности характеристик
полезных и мешающих воздействий, что делает эти системы неэффективными.
Наиболее эффективным способом преодоления априорной неопределенности условий функционирования системы автоматического сопровождения цели является построение системы, инвариантной (нечувствительной) или квазиинвариантной (слабочувствительной) к изменению этих условий. Для достижения этого применяют способ уменьшения ошибок слежения за счет применения связей, при которых кроме входных сигналов, являющихся функцией ошибки управления, используются также входные сигналы, зависящие от полезных (задающих) или мешающих (помеховых) воздействий.
Анализ способов комплексного использования измерительной информации, позволил сделать вывод, что инвариантность к задающему воздействию следящей системы можно обеспечить путем комплексирования ее с автономными измерителями (датчиками) этих воздействий. Комплексирование активно-пассивных локационных каналов обеспечивает независимость момента коррекции ошибки системы сопровождения с помощью одного из измерителей (датчиков), возможность получения более точной информации от нескольких измерителей по сравнению с одним из них, а также повышение уровня помехозащищенности (скрытности и помехоустойчивости) следящей системы.
Достижение требуемого порядка
астатизма следящей системы осуществлено на основе теории комплексирования автоматических
систем с введением дополнительной информации от корректирующего канала (КК) в
контур слежения основного канала (ОК).
Обобщенная структура такой системы представлена на рисунке 1, где ОКП – операторный
коэффициент передачи.
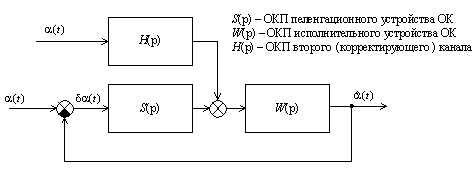
Рисунок 1 – КССО
с введением дополнительной информации в контур слежения ОК, здесь КССО – комплексированная
система
сопровождения воздушных объектов
Динамика системы описывается системой уравнений (1), где 
.Так как решается задача обеспечения инвариантности к задающему
(полезному) воздействию 
, мешающие воздействия в этих уравнениях не
учитываются,
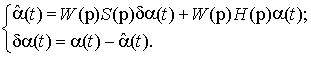(1)
Тогда ОКП КССЦ по задающему воздействию
, (2)
.
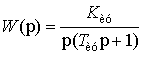Условие инвариантности, при котором 
воспроизводится в
системе без искажений, это
. (3)
Для достижения абсолютной инвариантности
КССО ОКП корректирующего канала 
должен быть обратным 
, что физически не реализуемо, так как степень полинома числителя
оказывается больше степени полинома знаменателя. Заменой физически нереализуемого
ОКП КК по задающему воздействию близким к нему, но физически реализуемым, можно
получить квазиинвариантную (КИ) следящую систему, мало отличающуюся от абсолютно
инвариантной системы. Это ведет к определенному проигрышу в точности следящей
системы по сравнению с абсолютно инвариантной.
Для уменьшения
этого проигрыша используют способ подключения сигнала КК в контур слежения ОК
через оптимальный согласующий (СФ) фильтр с ОКП 
, требующего определения.
В общем случае, динамика системы (рисунок 2), без учета мешающих воздействий
(возмущений, помех), описывается системой уравнений
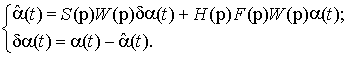(4)
Подстановкой второго уравнения системы (4) в первое
,
и тогда ОКП 
КССО в замкнутом
состоянии (по оценке 
)
. (5)
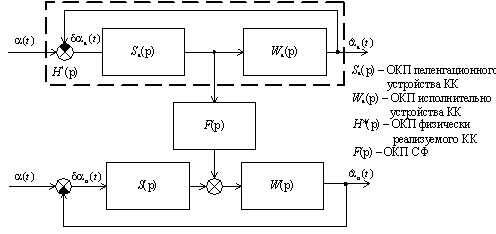
Рисунок 2 – Структурная схема математической
модели КССО (с заданной структурой корректирующего канала)
Поскольку ОКП следящей системы по ошибке и по оценке
задающего воздействия связаны соотношением 
, то с учетом (5)
. (6)
Представляя ОКП всех функциональных устройств КССО в виде
отношения полиномов (многочленов)
,(7)
с учетом (7)
=
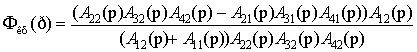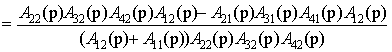. (8)
Так как решается задача синтеза квазиинвариантной
КССО при заданных структурах и
параметрах ОК и КК (когда оптимизируются только параметры СФ между каналами),
то с учетом переобозначений полиномов, определяющих функциональные устройства
КССО с фиксированными параметрами,
; (9)
,
выражение (8) принимает вид
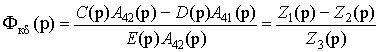. (10)
Все составляющие числителя и знаменателя в (10) могут быть представлены в виде
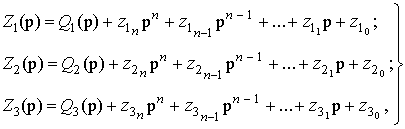(11)
где 
, 
, 
– части полиномов со степенью, большей n, а
коэффициенты полиномов
, 
, 
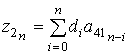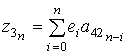. (12)
Обеспечением в (10) путем оптимизации параметров СФ
(которые содержатся в полиномах 
и 
) равенство нулю числителя, достигается абсолютная инвариантность
системы сопровождения, что физически нереализуемо. Единственный подход к достижению
квазиинвариантности системы является повышение порядка ее астатизма до заданной степени.
Для повышения порядка астатизма КИ КССО до n-го
порядка (повышения точности следящей системы) требуется выполнение условия
равенства соответствующих коэффициентов полиномов 
и 
,
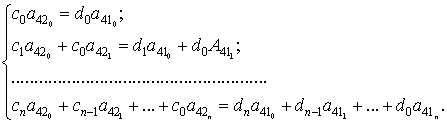(13)
Из (13) следует, что конкретное значение, на которое
может быть повышен порядок астатизма КИ КССО, зависит от порядка полиномов
числителя и знаменателя физически реализуемого оптимального СФ между ОК и КК (рисунок 2).
Так как система (13) имеет в левой и правой частях
неизвестные коэффициенты полиномов 
и 
, то ее решение в явном виде отсутствует. Для получения
оптимального решения системы (13), требуется задание конкретных значений коэффициентов
одного из полиномов (либо 
, либо 
), например, коэффициентов 
.
Подставляя это в
(13), 
и
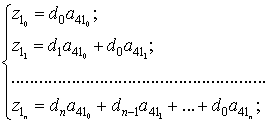(14)
Решением системы (14) в векторно-матричном находятся
коэффициенты 
,
(15)
где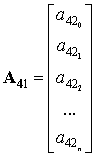 
, 
, 
.
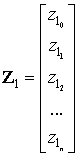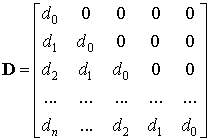Таким
образом, реализация математических выражений (1–15) дает возможность достичь требуемый порядок астатизма у
комплексированной системы. С учетом рассмотренных математических выкладок была
разработана методика синтеза квазиинвариантной активно-пассивной комплексированной
системы сопровождения цели.
Методика
включает следующие этапы (рисунок 3).
На
начальном этапе производится:
задание
исходных данных (рассматривается малоразмерная воздушные объекты, находящаяся в
зоне поражения войсковых зенитных комплексов ближнего действия; ЗК функционируют в широком диапазоне изменения угловой
скорости линии визирования цели и спектральной плотности мощности АШП; рассматриваются
штатная активная радиолокационная станция сопровождения ВО, с применением режимов максимально возможной скрытности,
следящие тепловой оптический визир и ТПВ, оптические (видимого и инфракрасного
диапазонов) и радиолокационные пеленгаторы; оси всех пеленгаторов жестко
съюстированы; задачи обнаружения, отождествления и захвата воздушных объектов
на сопровождение решены);
выбор типов комплексируемых локационных каналов в составе КССО, при котором выполняется выделение в составе КССО основного канала (в частности, типового следящего РЛ координатора цели, функционирующего в условиях воздействия АШП и в режимах, обеспечивающих максимально возможную его скрытность) и выбор дополнительно к основному, одного из корректирующих каналов, в минимальной степени подверженного воздействию заданного типа помех (в частности, оптического локационного канала).
Далее
на этапе синтеза определяется
критерий оценки качества синтезируемой КИ КССО в виде минимизации суммарной
ошибки сопровождения цели путем минимизации ее динамической составляющей без
увеличения ее случайной составляющей.
, 
,
где 
– суммарная ошибка
сопровождения комплексированной системы, 
, 
– динамическая и
флюктуационная составляющие суммарной ошибки комплексированной системы, 
– флюктуационная
составляющая ошибки сопровождения основного канала; 
– независимость от
задающего воздействия,
– спектральная плотность (СПМ) мощности АШП в ОК и j-м КК соответственно, 
–допустимая СПМ АШП в j-м КК.
Осуществляются
структурный синтез:
синтез
структуры комплексированной системы, согласующего фильтра между основным и
корректирующим каналами для обеспечения инвариантности КССО к закону изменения угловой скорости линии визирования цели;
определение
ограничений на физическую реализуемость синтезированного согласующего фильтра.
При
параметрическом синтезе производятся:
оптимизация
параметров согласующего фильтра СФ между основным и корректирующим каналами,
включающая процедуры определения оптимальных значений коэффициентов передачи и
постоянных времени СФ для требуемого повышения порядка астатизма системы;
представления
операторного коэффициента передачи оптимального СФ в виде произведения его
типовых динамических звеньев.
На основе методики осуществлен синтез структуры
активно-пассивной
квазиинвариантной оптико-радиолокационной комплексированной системы сопровождения
воздушных объектов в ЗК БД (рисунок 4).
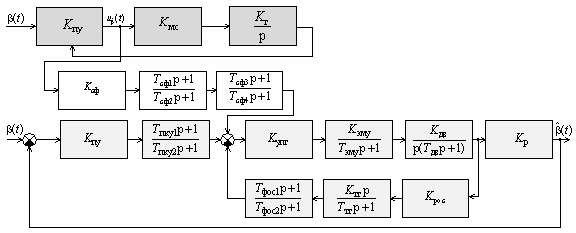
Рисунок 4 – Структурная
схема математической модели активно-пассивной квазиинвариантной оптико-радиолокационной комплексированной
системы сопровождения ВО в ЗК БД
В качестве прототипов локационных каналов КИ КССО
использованы два канала с астатизмом первого порядка каждый – канал угловой
автоматики СС ВО БМ 9А33БМ3 (рисунок 4, блоки выделенные светло-серым
цветом, где ПУ – пеленгационное устройство; ПКУ – последовательное
корректирующее устройство; УПТ – усилитель постоянного тока; ЭМУ – электромашинный
усилитель; ДВ – двигатель; Р – редуктор; РОС – редуктор обратной связи; ТГ – тахогенератор;
ФОС – фильтр в цепи обратной связи) и следящий КЦ с гироскопическим приводом,
используемый в оптико-электронных ГСН войсковых ЗК (рисунок 4, темно-серым цветом,
где ПУ – пеленгационное устройство, МС –
магнитная система; Г – гироскопический привод).
Постоянные операторных коэффициентов передач (ОКП) канала
угловой автоматики ССО БМ 9А33БМ3 имеют значения:
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
;
.
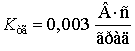Постоянные операторных коэффициентов передач (ОКП) следящего
КЦ с гироскопическим приводом, используемого в оптико-электронных ГСН войсковых ЗК, имеют значения:
; 
;
.
Исходя из условия повышения астатизма системы АСН на два
порядка, результатом синтеза
оптимального фильтра, как произведение ОКП типовых динамических звеньев,
.
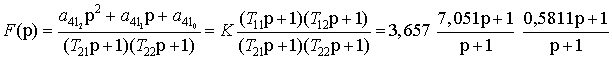Для оценки качества синтезируемой КИ КССО разработана и исследована имитационная цифровая модель (ЦМ) основного канала (рисунок 5) КССО и КИ КССО в целом (рисунок 6) при маневре ВО в условиях шумовых и помеховых воздействий.
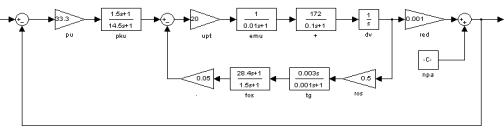
Рисунок 5 – Имитационная
цифровая модель основного канала КССО (РЛ СС
ВО ЗРК 9К33БМ3)
Путем имитационного моделирования исследовалось качество функционирования ОК КССО (типовой РЛ системы АСН) и КИ КССО в условиях АШП, с учетом влияния углового шума, по результатам которого осуществлена оценка их эффективности.
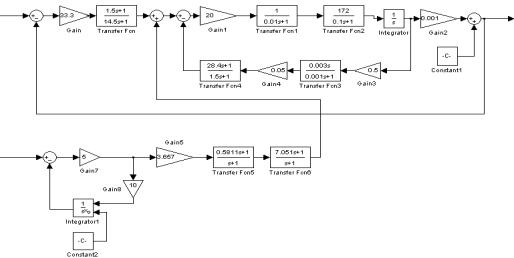
Рисунок 6 – Имитационная
цифровая модель КИ КССО
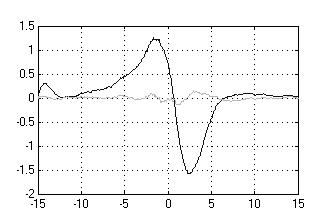
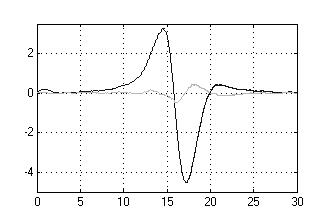
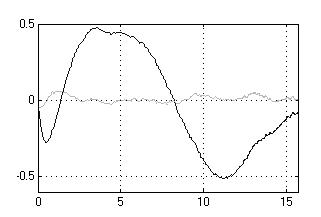
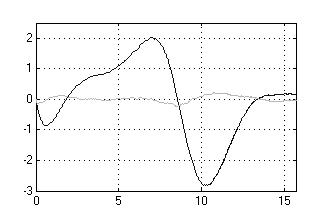
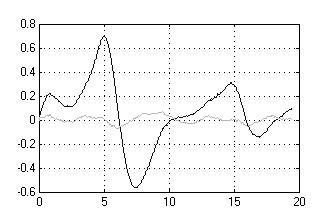
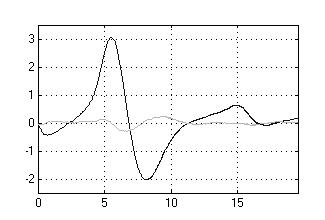
На рисунке 7, 8 и 9
представлены соответственно графики закона изменения ошибок сопровождения
имитационной модели ОК КССО и КИ КССО при прямолинейном движении ВО (ПДО), при
маневрах «вираж» и «змейка», где в подрисуночных подписях vц – скорость объекта, Рц – курсовой
параметр ВО; Dцт – расстояние до центра
окружности, по которой ВО совершает вираж, Rц – радиус дуги окружности, по которой совершается
вираж; Yц – расстояние до прямой,
относительно которой совершается маневр «змейка», Aц – максимальное отклонение объекта от заданной
прямой, Т – расстояние между точками
максимального отклонения ВО от прямой относительно которой совершается маневр
«змейка».
|
|
|
||||||||
|
а |
б |
||||||||
|
Рисунок 7 – Ошибки
сопровождения ПДО при АШП высокой интенсивности: а)
vц = 300 м/с, Рц = 1000 м, Ωβ
= 0,3 рад/с; б) vц = 300 м/с, Рц = 600 м, Ωβ
= 0,5 рад/с. |
|||||||||
|
|
|
||||||||
|
а |
б |
||||||||
|
Рисунок 8 – Ошибки
сопровождения ВО при маневре «вираж» при АШП высокой интенсивности:
а)
vц = 300 м/с, Dцт = 2500 м, Rц = 1000 м; б) vц = 300 м/с, Dцт = 4500 м, Rц = 1000 м. |
|||||||||
|
|
|
||||||||
|
а |
б |
||||||||
|
Рисунок 9 –Ошибки
сопровождения ВО при маневре «змейка» при АШП высокой интенсивности а)
vц = 300 м/с, Yц = 2500 м, Aц = 1000 м, Т = 4000 м, б)
vц = 300 м/с, Yц = 4500 м, Aц = 1000 м, Т = 4000 м |
|||||||||
Анализ результатов имитационного моделирования, представленных на рисунках 7–9 показывает, что синтезированная на основе разработанной методики активно-пассивная квазиинвариантная комплексированная система сопровождает маневрирующие воздушные объекты в условиях АШП высокой интенсивности на порядок точнее, чем штатная ССЦ, обеспечивая попадание ошибки сопровождения ВО на линейный участок пеленгационной характеристики пеленгационного устройства РЛ системы автоматического сопровождения по направлению (область пространства на рисунках 7–9 заключенная между штриховыми линиями и включающая в себя ось времени). Этим достигается более устойчивое сопровождение малоразмерных маневрирующих ВО. Несмотря на то, что отношение максимумов ошибок сопровождения штатной ССО и КИ КССО для различных маневров ВО имеет различные значения, в пределах одного вида маневра оно в среднем одинаково. Это указывает на снижение зависимости ошибки сопровождения целей комплексированной системой от параметров их маневра и подчеркивает ее квазиинвариантные свойства.
Литература
1.
Зайцев Г. Ф. Теория инвариантности и комбинированное
управление в автоматических системах. Киев, КВИРТУ, 1961. 62 с.
2.
Первачев С. В. Радиоавтоматика. М., Радио и связь, 1982.
296 с.
3. Авласенок А. В.
Спец. тема: Дис. ... канд. техн. наук. Смоленск. ВА ПВО СВ РФ, 1994. 226 с.
PROCEDURES
FOR THE SYNTHESIS OF QUASI-INVARIANT COMPLEXING AIRBORN TARGETS TRACKING SYSTEM
Savitsky
F. L., Vasilchenko O. V., Muravsky A. P.
The
paper presents procedures for the synthesis of complexing automatic airborne targets
tracking system, which achieved the required order astatism through the organization
of an optimal connection between complexing locational channels.
Key words: procedures, complexation, high speed small-sized airborne targets,
tracking accuracy, astaticism system level.
Военная академия войсковой ПВО Вооруженных Сил
Российской Федерации имени Маршала Советского Союза
А. М. Василевского (ВА ВПВО ВС РФ)
Поступила в редакцию 7.06.2013.