Способы параллельного решения систем дифференциальных уравнений с нечеткими параметрами

Ó 2013 г. Зернов М. М., Карелина Е. С.

В данной статье рассматриваются варианты параллельной организации вычислений при решении систем обыкновенных дифференциальных уравнений первого порядка с нечеткими начальными условиями на основе метода, предложенного Обергуггенбергером и Пицманом в статье «Дифференциальные уравнения с нечеткими параметрами». Предложены два варианта: способ решения систем ОДУ с нечёткими НУ с последовательной подготовкой и параллельным решением вариантов чёткой задачи и способ решения систем ОДУ с нечёткими НУ с параллельным составлением и решением вариантов чёткой задачи.

Ключевые слова: обыкновенные дифференциальные уравнения первого порядка, метод Обергуггенберга и Пицмана.

1. Задача и метод решения систем обыкновенных дифференциальных уравнений первого порядка с нечеткими начальными условиями

Многие системы, особенно динамические, описываются системами обыкновенных дифференциальных уравнений первого порядка. При этом, на момент анализа этих систем далеко не все параметры уравнений определены точно. Вместо точных значений параметров присутствуют их нечеткие значения, которые характеризуют лишь области возможных значений этих параметров с некоторыми уровнями риска.

В работе [1] предлагается метод решения систем обыкновенных дифференциальных уравнений первого порядка с нечеткими начальными условиями на основе многократного решения систем с четкими параметрами, представляющими собой варианты реализации вектора нечетких параметров. В данном методе вычисление функции принадлежности функции решения происходит следующим образом:

1. Задаем отрезок t, на котором будем искать решение;

2. Задаем вид функции принадлежности и ее параметры для каждой нечеткой переменной;

3. Задаем количество интервалов разбиения значения функции принадлежности;

4. Задаем шаги дискретизации отрезка t, функции принадлежности;

5. Задаем начальное значение t;

6. Задаем α-уровень;

7. Определяем границы заданного α-уровня для каждой нечеткой переменной;

8. Задаем шаги дискретизации значений нечетких переменных на данном α-уровне;

9. Вычисляем всевозможные значения нечетких переменных на данном α-уровне;

10. Составляем таблицу всевозможных сочетаний значений нечетких переменных на данном α-уровне;

11. Для всех сочетаний значений нечетких переменных на данном α-уровне вычисляем значение решения при заданном t;

12. Находим границы заданного α-уровня для решения при заданном значении t как минимум и максимум значений функции решения на данном α-уровне. В [1] рекомендуется применять сплайновую интерполяцию с целью уменьшения числа вариантов четких векторов параметров, но она может приводить к существенным ошибкам.

13. Выполняем п.7-п.12 для каждого значения функции принадлежности;

14. Выполняем п.6-п.13 для каждого значения t;

15. Этап дополнительной обработки. Пробегаем по всем значениям границ α-уровней от 0 до 1 для функции решения. Если границы следующего α-уровня шире, чем границы предыдущего α-уровня, то берем в качестве границ для следующего α-уровня значения границ предыдущего α-уровня.

16. Выводим результат работы приложения, т. е. функцию принадлежности для решения.

Приведем пример решения системы уравнений. Зададим систему уравнений с начальными условиями:

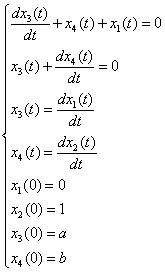
Получаем решение в общем виде:

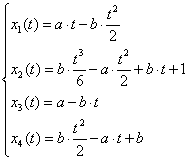
Для полученного решения системы задаем вид и параметры нечетких начальных условий:

1) для нечеткого начального условия a – вид функции принадлежности треугольный, ее параметры (1;3;5) (см. рис. 1);

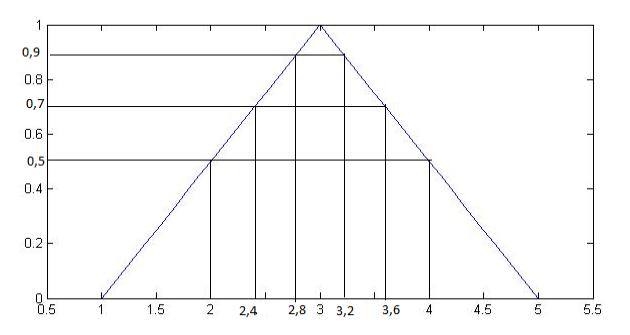
Рисунок 1 – Функция принадлежности для нечеткого параметра a

2) для нечеткого начального условия b: вид функции принадлежности –гауссова, ее параметры (5;2) (см. рис. 2);

Задаем отрезок t: [0;10], номер функции 3, количество интервалов разбиения функцийпринадлежности 5.

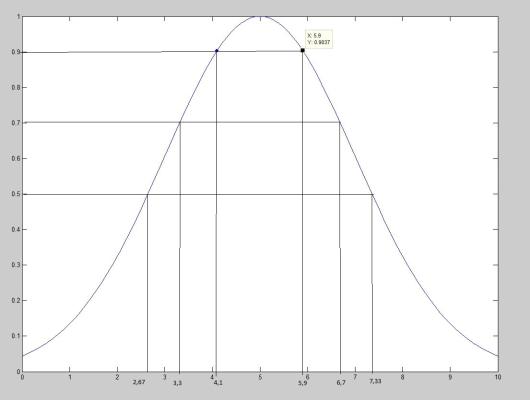
Рисунок 2 –Функция принадлежности для нечеткого параметра b

Границы многомерных областей, изображенные на рисунке 3, для α-уровня 0,5 – синим цветом, 0,7 – зеленым цветом, 0,9 – красным цветом выглядят следующим образом:

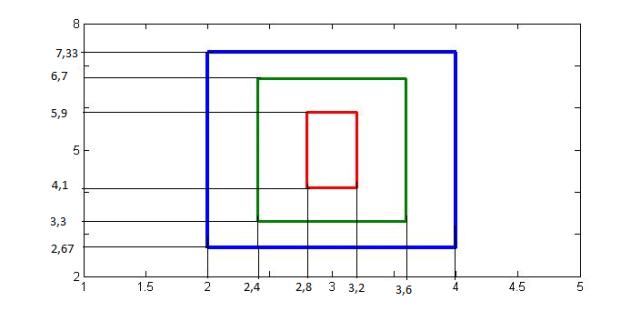
Рисунок 3 – Границы многомерных областей для α-уровней 0.5, 0.7, 0.9

Пробегая по всем значениям нечетких параметров и переменной t, получим вид функции принадлежности третьей функции решения на отрезке [0; 2], изображенный на рисунке 4.

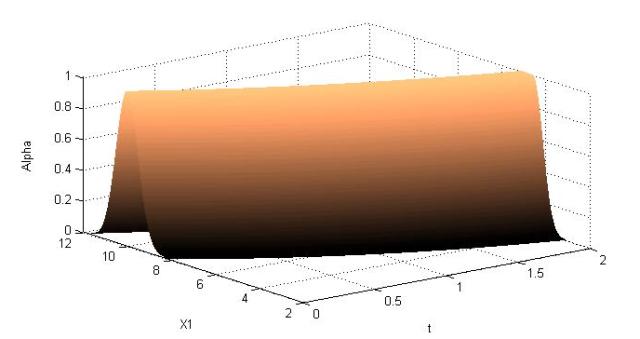
Рисунок 4 –Вид функции принадлежности функции решения

2. Способ решения систем ОДУ с нечёткими НУ с последовательной подготовкой и параллельным решением вариантов чёткой задачи

Рассмотренный метод решения систем ОДУ первого порядка с нечеткими начальными условиями обладает естественным параллелизмом по данным, что позволяет предложить параллельные варианты алгоритма, рассмотренного в [1].

Ниже предложен способ параллельной реализацииметода решения ОДУ первого порядка с нечеткими начальными условиями в заданном временном интервале, отличающийся предварительным построением всех вариантов реализации вектора нечетких начальных условий для всех анализируемых моментов времени:

- задаем вид функции принадлежности и ее параметры для каждого нечеткого коэффициента;

- задаем интервал t для построения графиков и дискретизируем t;

- задаем дискретность α-уровней;

- разбиваем границу многомерной области, соответствующей α-уровням на эквидистантные участки;

- составляем матрицу всевозможных сочетаний значений t и всех нечетких начальных условий для всех α-уровней;

- параллельно вычисляем значение функции решения для всех наборов переменных;

- находим максимум и минимум значений функции решения для каждого α-уровня и каждого значения t;

- этап дополнительной обработки: пробегаем по всем значениям границ α-уровней от 0 до 1 для функции решения. Если границы следующего α-уровня шире, чем границы предыдущего α-уровня, то берем в качестве границ для следующего α-уровня значения границ предыдущего α-уровня.

- получаем функцию принадлежности решения.

Матрица всевозможных сочетаний значений t и всех значений нечетких начальных условий для всех α-уровней описана таблицей 1:

Таблица 1 – Матрица всевозможных сочетаний значений t и всех значений нечетких начальных условий для всех α-уровней

Зачение t	α-уровень[0]	Значение функции решения	α-уровень[1]	Значение функции решения	…	α-уровень[s]	Значение функции решения
t[0]	Всевозможные сочетания значений нечетких начальных условий		Всевозможные сочетания значений нечетких начальных условий			Всевозможные сочетания значений нечетких начальных условий
t[1]	Всевозможные сочетания значений нечетких начальных условий		Всевозможные сочетания значений нечетких начальных условий			Всевозможные сочетания значений нечетких начальных условий
…	…
t[n]	Всевозможные сочетания значений нечетких начальных условий		Всевозможные сочетания значений нечетких начальных условий			Всевозможные сочетания значений нечетких начальных условий

Варианты реализации вектора нечетких начальных условий для дискретного разбиения границы заданного α-уровня, где k нечетких начальных условий, m точек для каждого начального условия на α-уровне,описана таблицей 2:

Таблица 2 - Варианты реализации вектора нечетких начальных условий для дискретного разбиения границы заданного α-уровня

NP¹₀	NP¹₁	…	NP¹_k
NP²₀	NP¹₁	…	NP¹_k
NP³₀	NP¹₁	…	NP¹_k
…
NP^m₀	NP²₁	…	NP¹_k
NP¹₀	NP¹₁
…
NP^m₀	NP^m₁	…	NP^m_k

Таким образом, для каждому значению t в таблице всевозможных сочетаний значений переменных для функции решения будет соответствовать m^k строк сочетаний значений нечетких начальных условий. Тогда, если на отрезке t имеем n значений этой переменной, то каждому значению α-уровня будет соответствовать подтаблица сочетаний значений t и нечетких начальных условий из (m^k)ⁿ строк.

В столбце значение функции решения будут находиться значения функции решения для каждого сочетания значений переменных. Затем для каждого значения tбудет найдено максимальное и минимальное значение функции решения. Таким образом, будут получены границы функции принадлежности для функции решения для всех значений t и всех α-уровней, т.е. получена функция принадлежности решения. Матрица выходных данных описана таблицей 3:

Таблица 3 – Матрица выходных данных

Значение t	α-уровень[0]	Значение функции решения	α-уровень[1]	Значение функции решения	…	α-уровень[s]	Значение функции решения
1	2	3	4	5	6	7	8
t[0]	Вариант вектора нечетких начальных условий, при котором значение функции решения минимально	Минимальное значение функции решения при заданном t и заданном α-уровне	Вариант вектора нечетких начальных условий, при котором значение функции решения минимально	Минимальное значение функции решения при заданном t и заданном α-уровне	…	Вариант вектора нечетких начальных условий, при котором значение функции решения минимально	Минимальное значение функции решения при заданном t и заданном α-уровне
	Вариант вектора нечетких начальных условий, при котором значение функции решения максимально	Максимальное значение функции решения при заданном t и заданном α-уровне	Вариант вектора нечетких начальных условий, при котором значение функции решения максимально	Максимальное значение функции решения при заданном t и заданном α-уровне	…	Вариант вектора нечетких начальных условий, при котором значение функции решения максимально	Максимальное значение функции решения при заданном t и заданном α-уровне
t[1]	Вариант вектора нечетких начальных условий, при котором значение функции решения минимально	Минимальное значение функции решения при заданном t и заданном α-уровне	Вариант вектора нечетких начальных условий, при котором значение функции решения минимально	Минимальное значение функции решения при заданном t и заданном α-уровне	…	Вариант вектора нечетких начальных условий, при котором значение функции решения минимально	Минимальное значение функции решения при заданном t и заданном α-уровне
	Вариант вектора нечетких начальных условий, при котором значение функции решения максимально	Максимальное значение функции решения при заданном t и заданном α-уровне	Вариант вектора нечетких начальных условий, при котором значение функции решения максимально	Максимальное значение функции решения при заданном t и заданном α-уровне	…	Вариант вектора нечетких начальных условий, при котором значение функции решения максимально	Максимальное значение функции решения при заданном t и заданном α-уровне
…
t[n]	Вариант вектора нечетких начальных условий, при котором значение функции решения минимально	Минимальное значение функции решения при заданном t и заданном α-уровне	Вариант вектора нечетких начальных условий, при котором значение функции решения минимально	Минимальное значение функции решения при заданном t и заданном α-уровне	…	Вариант вектора нечетких начальных условий, при котором значение функции решения минимально	Минимальное значение функции решения при заданном t и заданном α-уровне
	Вариант вектора нечетких начальных условий, при котором значение функции решения максимально	Максимальное значение функции решения при заданном t и заданном α-уровне	Вариант вектора нечетких начальных условий, при котором значение функции решения максимально	Максимальное значение функции решения при заданном t и заданном α-уровне	…	Вариант вектора нечетких начальных условий, при котором значение функции решения максимально	Максимальное значение функции решения при заданном t и заданном α-уровне

На рисунке 5 представлена схема рассмотренного способа в виде диаграммы деятельностей нотации UML:

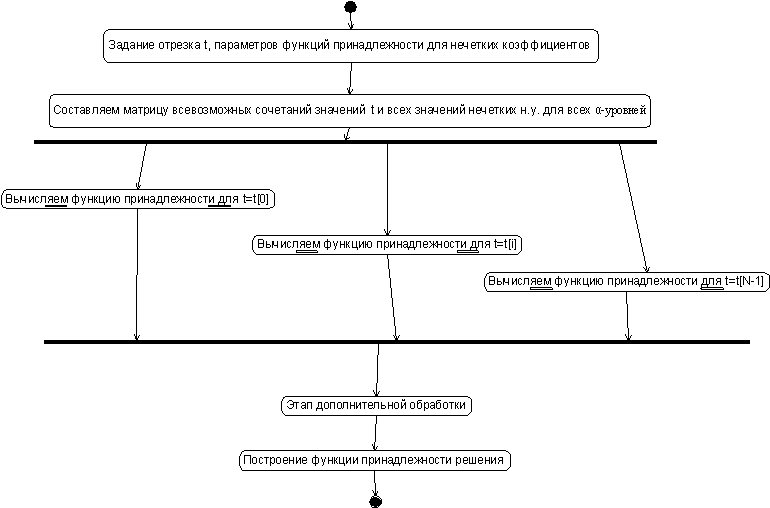
Рисунок 5 – Общая схема параллельной программы

3. Способ решения систем ОДУ с нечёткими НУ с параллельным составлением и решением вариантов чёткой задачи

Выше описан способ вычислений функции принадлежности для функции решения, в котором лишь один этап выполняется параллельно, а именно: вычисление значений функции решения при разных наборах значений нечетких НУ и t.

Можно организовать вычислений иначе. Этап составления всевозможных сочетаний значений t и нечетких НУ включить в этап разбиения границ многомерных областей, соответствующих α-уровням. При этом как только появляется очередной набор значений переменных, вычислять значение функции решения. После вычисления значений функции решения для всех наборов переменных для соответствующего α-уровня и значения t выбирать минимальное и максимальное из них.

Разбиение границ многомерных областей, соответствующих α-уровням тоже можно проводить параллельно по всем значениям α-уровней.

Тогда способрешения систем ОДУ с нечёткими НУ принимает вид:

- для функции решениязадаем виды и параметры для всех нечетких коэффициентов;

- задаем интервал t и шаг для t, дискретность α-уровней;

- параллельно для каждого значения t и каждого α-уровня разбиваем границу многомерной области на эквдистантные участки;

- параллельно составляем очередное сочетание значений переменных и вычисляем для него значение функции решения;

- выбираем минимальное и максимальное значение функции решения для всех α-уровней и всех значений t;

- проводим этап дополнительной обработки результатов;

- получаем функцию принадлежности для функции решения.

На рисунке 6 представлена общая схема способа в виде диаграммы деятельностей нотации UML:

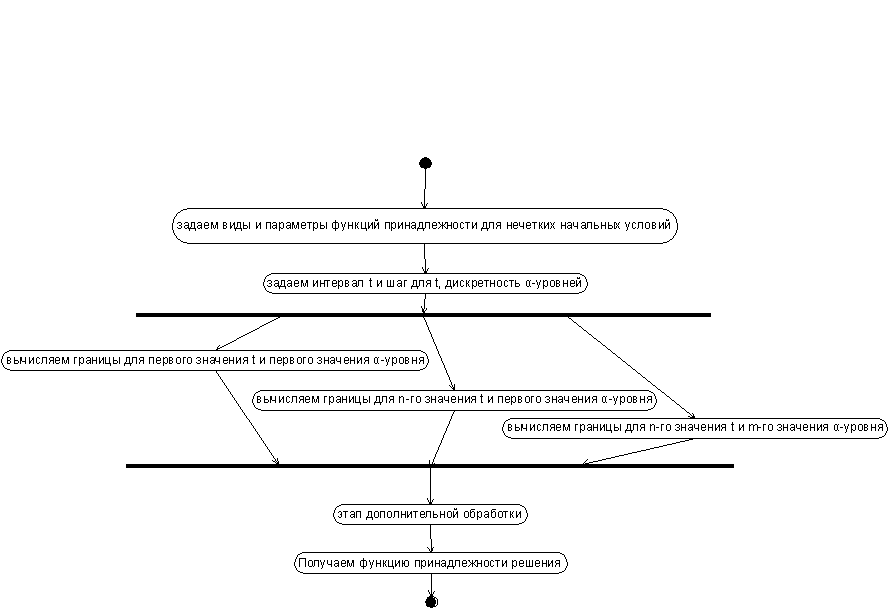
Рисунок 6 – Общая схема второго варианта параллельной программы

Этап вычисления границ α-уровней для функции решения изобразим подробнее на рисунке 7:

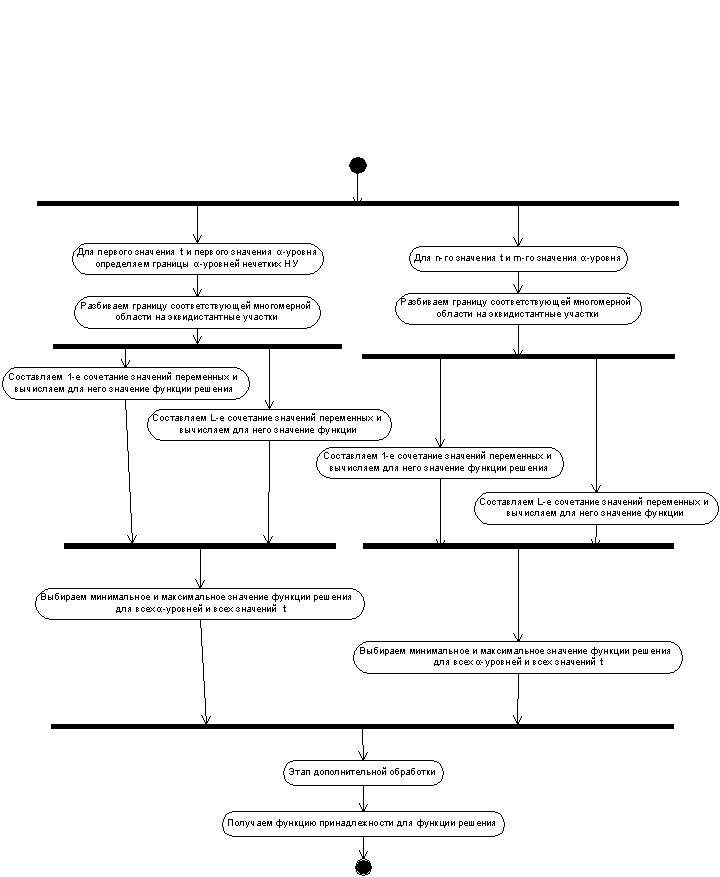
Рисунок 7 – Общая схема этапа вычисления границ α-уровней для функции решения

Заключение

В статье предложено 2 основных способа параллельной реализации метода решения систем дифференциальных уравнений 1-го порядка с нечёткими начальными условиями.

1. Способ решения систем ОДУ с нечёткими НУ, отличающийся последовательной подготовкой и параллельным решением вариантов чёткой задачи. Позволяет используя быстрый ЦП подготовить все данные для параллельной обработки на GPU.

2. Способ решения систем ОДУ с нечёткими НУ, отличающийся параллельным составлением и решением вариантов чёткой задачи. Позволяет увеличить быстродействие за счет подготовки исходных данных и решения задачи на одном устройстве и при этом не хранить большие объёмы промежуточной информации.

Эффективность рассмотренных вариантов параллельных способов решения обыкновенных дифференциальных уравнений будет существенно зависеть как от особенностей аппаратной платформы, так и от алгоритмической реализации. В настоящий момент способы реализуются на базе GPU с применением библиотек OpenCL.

литература

1. Oberguggenberger M., Pittschmann S. Differential equations with fuzzy parameters. // Mathematical and Computer Modeling of Dynamical Systems, 5:181-202, 1999. http://techmath.uibk.ac.at/numbau/publications/98-2.ps

METHOD OF PARALLEL ALGORITHMS FOR solving systems of ordinary differential equations with fuzzy initial conditions

Zernov M. M., Karelina E. S.

This article discusses the variants of parallel algorithms for solving systems of ordinary differential equations of the first order with fuzzy initial conditions based on the method proposed by Oberguggenberger and Pittschmannin the article "Differential equations with fuzzy parameters." Two variants were offered: the way for solving systems of ordinary differential equations with fuzzy initial conditions with serialpreparing and parallel solution of strict problem variants and the way for solving systems of ordinary differential equations with fuzzy initial conditions using parallel preparation and parallelsolvingof strict problem variants.

Key words: ordinary differential equations of the first order, method of Oberguggenberger and Pittschmannin.

Кафедра вычислительной техники

Филиал федерального государственного бюджетного образовательного

учреждения высшего профессионального образования

«Национальный исследовательский университет «МЭИ»

в г. Смоленске

Поступила в редакцию 13.05.2013.