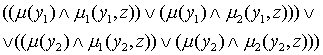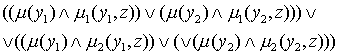Поступила в редакцию

Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 12. -

Вып. 3. - 2013. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-39-html/TITL-39.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-39-html/cont.htm

УДК 681.3

ИСПОЛЬЗОВАНИЕ ОПЕРАЦИЙ КОМПОЗИЦИИ И ОБЪЕДИНЕНИЯ НЕЧЕТКИХ МНОЖЕСТВ И ОТНОШЕНИЙ ДЛЯ АНАЛИЗА НЕЧЕТКИХ РЕЛЯЦИОННЫХ КОГНИТИВНЫХ КАРТ

Ó 2013 г. Федулов А. С.

(fedulov.doc)

Ключевые слова. Нечеткая реляционная когнитивная карта, нечеткие множества и отношения, нечеткая композиция, нечеткое объединение.

Введение

В работе [1] была предложена модель нечеткой реляционной когнитивной карты (НРКК), в которой состояния (значения) концептов представлены нечеткими множествами, а отношения между ними – нечеткими бинарными отношениями. Нечеткая реляционная когнитивная карта может быть задана в виде матрицы нечетких отношений (МНО):

(1)

где () – отношения между концептом и концептом , N – общее число концептов в НРКК.

В работе [2] был предложен подход к анализу НРКК с использованием операций с МНО, представленной в виде (1). В этой работе было также показано, что реализация этого подхода требует использования следующего набора операций над нечеткими множествами и отношениями.

1. Операция «умножения» нечетких отношений:

(2)

2. Коммутативная и ассоциативная операция «агрегирования» нечетких отношений между двумя концептами:

(3)

3. Операция «умножения» нечеткого множества на нечеткое отношение:

(4)

где , – нечеткие множества, представляющие нечеткие значения (состояния) концептов НРКК.

4. Коммутативная и ассоциативная операция «агрегирования» нечетких множеств, относящихся к одному концепту:

(5)

Для вышеуказанных операций должны быть определены нейтральные и поглощающие элементы.

Предложенные в [2] операции (2)– (5) носят абстрактный характер, что оставляет большие возможности для выбора и проектирования их конкретной реализации в соответствии с требуемым характером передачи и накопления влияний в НРКК.

Ограничением, накладываемым на конкретную реализацию операций (2)– (5), являются определенные в [2] необходимые совместные алгебраические свойства этих операций:

, где , – нечеткие множества, – нечеткое отношение;	(6)
, где – нечеткое множество, , – нечеткие отношения;	(7)
, где – нечеткое множество, , – нечеткие отношения.	(8)

Отметим, что требуемые алгебраические свойства формировались без каких-либо ограничений, накладываемых на операнды – нечеткие множества и отношения.

Практическое использование метода анализа НРКК, основанного на операциях (2)– (5), требует, прежде всего, их конкретизации. При этом необходимые алгебраические свойства должны быть выполнены.

В данной работе рассматривается возможность реализации операций (2)– (5) на основе операций композиции и объединения нечетких множеств и отношений.

1. Выбор вида операций над нечеткими множествами и

отношениями

1) В качестве операции умножения «» бинарных нечетких отношений предлагается использовать операцию композиции нечетких бинарных отношений на основе t- и s-норм [3], являющуюся нечетким расширением композиции обычных функций: . Такая операция эвристически наилучшим образом соответствует свойствам и особенностям отношений влияния, используемых в когнитивных картах, а также наиболее полно отражает механизм передачи нечеткого влияния между концептами.

Пусть и - два нечетких бинарных отношения с функциями принадлежности и . - переменные соответствующих базовых множеств. Тогда s-t-композиция представляет собой нечеткое бинарное отношение: , имеющее функцию принадлежности:

(9)

где операция «Ú» - s-норма, а «Ù» - t-норма.

2) В качестве операции умножения «» нечеткого множества на нечеткое отношение будем использовать нечеткую композицию нечеткого множества и нечеткого бинарного отношения.

Пусть - нечеткое множество с функцией принадлежности , а - нечеткое бинарное отношение с функцией принадлежности . - переменные соответствующих базовых множеств. Тогда результат композиции представляет собой нечеткое множество, имеющее функцию принадлежности:

(10)

3) В качестве операции агрегирования «Å» нечетких отношений между двумя концептами будем использовать операцию объединения нечетких бинарных отношений (элементов МНО) на основе s-нормы.

Пусть и - два нечетких бинарных отношения с функциями принадлежности и . . Тогда агрегирование двух нечетких бинарных отношений представляет собой нечеткое бинарное отношение: имеющее функцию принадлежности:

(11)

4) В качестве операций агрегирования «» будем использовать операцию объединения нечетких множеств на основе s-нормы. Пусть и - два нечетких множества с функциями принадлежности и . . Тогда агрегирование двух нечетких множеств представляет собой нечеткое множество, имеющее функцию принадлежности:

(12)

Нейтральные и поглощающие элементы для операций (9)–(12) проектируются исходя из свойств t- и s-норм, используемых в них.

2. Условия выполнимости алгебраических требований, предъявляемых к операциям над нечеткими множествами и отношениями

Выбор типов связок в выражениях (9)– (12) определяет довольно широкий их спектр, определяемый большим количеством разных s- и t-норм, используемых в теории нечетких множеств и обладающих разными свойствами [4]. Рассмотрим, какими свойствами должны обладать s- и t-нормы, для того, чтобы обеспечить выполнимость алгебраических требований, установленных в [2].

1) Очевидно, что коммутативность и ассоциативность операций агрегирования (11) и (12) выполняется при коммутативности и ассоциативности связки «Ú».

2) Относительно свойств (6)– (8) справедливо следующее утверждение:

Утверждение. Свойства (6)– (8) операций (2)– (5), реализованных в виде (9)– (12) выполняются, если t-норма дистрибутивна относительно s-нормы, а s-норма коммутативна и ассоциативна.

Доказательство.

Докажем утверждение для свойства (6).

Рассмотрим два нечетких множества , и нечеткое бинарное отношение: с функциями принадлежности, соответственно: . Требуется доказать равенство:

можно представить в виде:

(13)

можно представить в виде:

Дистрибутивность связки относительно связки позволяет представить (13) в виде:

(14)

Коммутативность и ассоциативность связки позволяет представить (14) в виде:

что доказывает утверждение.

Докажем утверждение для свойства (7).

Рассмотрим нечеткое множество и нечеткие бинарные отношения: , с функциями принадлежности, соответственно: . Требуется доказать равенство:

можно представить в виде:

(15)

Пусть t-норма дистрибутивна относительно s-нормы. Тогда выражение (15) можно представить в виде:

(16)

Рассмотрим выражение (16) в двух точках промежуточной переменной y: :

(17)

Если s-норма коммутативна и ассоциативна, то выражение (17) можно представить в виде:

(18)

Расширяя выражение (18) на все множество переменной , получим:

(19)

можно представить в виде:

(20)

Равенство выражений (19) и (20) доказывает утверждение.

Докажем утверждение для свойства (8).

Рассмотрим нечеткое множество: и нечеткие бинарные отношения: , с функциями принадлежности, соответственно: . Требуется доказать следующее равенство:

Выразим и с помощью операций над ФП:

,	(21)
.	(22)

При дистрибутивности связки «» относительно связки «Ú» выражение (21) можно представить в виде:

(23)

а выражение (22) – в виде:

(24)

В случае коммутативности и ассоциативности связки «Ú» выражения (23) и (24) равны между собой и могут быть представлены в виде:

Утверждение доказано.

Таким образом, необходимые требования, предъявляемые к s- и t-нормам, имеют вид:

1) ассоциативность и коммутативность s-нормы;

2) дистрибутивность t-нормы относительно s-нормы.

Как показано в [4], этим требованиям отвечает, например, связка максимум для s-нормы и связка минимум - для t-нормы.

Заключение

В работе исследована возможность использования операций композиции и объединения нечетких множеств и отношений для анализа нечетких реляционных когнитивных карт. Доказано, что предложенный набор операций удовлетворяет необходимым алгебраическим требованиям, если s-норма ассоциативна и коммутативна, а t-норма дистрибутивна относительно s-нормы. В этом случае операции композиции и объединения могут быть использованы для реализации предложенного в [2] подхода к анализу нечетких реляционных когнитивных карт.

Литература

1. Федулов, А. С. Нечеткие реляционные когнитивные карты / А. С. Федулов // Теория и системы управления.- 2005.- № 1.- С. 120- 132.

2. Федулов, А. С. Анализ нечетких реляционных когнитивных карт на основе векторно-матричных операций/ А. С. Федулов // Нейрокомпьютеры: разработка, применение. – 2009. № 8. – С. 44–48.

3. Кофман, А. Введение в теорию нечетких множеств / А. Кофман.- М. : Радио и связь, 1982.- 432 с.

4. Дюбуа, Д. Теория возможностей. Приложение к представлению знаний в информатике / Д. Дюбуа, А. Прад. - М. : Радио и связь, 1990.- 288 с.

USE OF OPERATIONS OF A COMPOSITION AND UNION OF FUZZY SETS AND RELATIONS FOR THE ANALYSIS OF FUZZY RELATIONAL COGNITIVE MAPS

Fedulov A. S.

Possibility of use of operations of a composition and union of fuzzy sets and relations for the analysis of fuzzy relational cognitive maps is investigated. It is proved, that the offered set of operations meets necessary algebraic requirements.

Key words. Fuzzy relational cognitive maps, fuzzy sets and relations, fuzzy composition, fuzzy union

Федулов Александр Сергеевич,

д.т.н., профессор,

Заведующий кафедрой вычислительной техники
филиала МЭИ в г. Смоленске,

fedulov_a@mail.ru

Кафедра вычислительной техники
Филиал ГБОУ ВПО «Национальный исследовательский университет «МЭИ»» в г. Смоленске

Поступила в редакцию 24.11.2013.