Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 12. -
Вып. 3. - 2013. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-39-html/TITL-39.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-39-html/cont.htm
УДК 311.211
рЕШЕНИЕ
СТАТИСТИЧЕСКОЙ ЗАДАЧИ оценки РАСХОДА ЖИДКОСТИ В ТЕХНОЛОГИЧЕСКОМ ПРОЦЕССЕ
Ó 2013 г. Делеговская Т. В., Найдёнов Е. В.
В работе описан процесс оценки и прогнозирования расходов питательной
жидкости в технологическом процессе обеспечения для заданных условий среды.
Набор статистических данных позволяет выработать рекомендации для дальнейшего
применения.
Ключевые слова: анализ, данные, жидкость, статистика,
формула.
Статистический анализ (СА) является
неотъемлемой составляющей при разработке и отладки нового оборудования. Как
правило, основной целью СА при анализе массива полученных первичных данных
является выработка рекомендаций и поиск оптимальной формулы для последующих
расчётов. Однако, основную сложность для проведения СА представляют особенности
протекания технологического процесса, либо сам исследуемый объект. В ряде
случаев необходимо предусмотреть ряд внешних факторов и иметь навыки понимания
их природы. Целью данной работы является описание процесса СА для формирования
оценки и прогнозирования расходов питательной жидкости в биологическом реакторе,
а также разработка оптимальной формулы учёта всех изменений в технологическом
процессе.
Для понимания составленной
технической задачи и проведения на её основе СА рассмотрим исследуемый
технологический процесс. Его блок-структура представлена на рисунке 1.
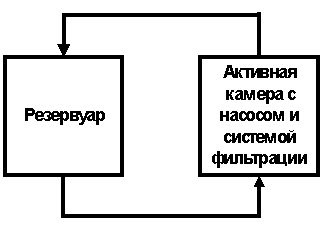
Рисунок 1 – Блок-структура
исследуемого процесса
Исследуемым объектом
является резервуар с питательной жидкостью. Исследуемый эффект – расчёт расхода
питательной жидкости с течением длительного времени с учётом технологических
факторов. Цель исследования – анализ статистических данных, первичная оценка,
прогнозирование и выработка оптимальной формулы для расчёта лимита времени в
течении которого в резервуаре будет сохраняться жидкость. Эксперимент, в ходе
которого составляется массив данных для исследований проводится в лабораторных
условиях и на математической модели.
В лабораторных условиях (см.
рисунок 2) в активной камере биологического реактора исследуется биохимический процесс.
Для этого резервуар с герметичной крышкой, заполняется известным уровнем питательной
жидкости и при помощи гибкой трубки соединяется с миниатюрным мотором. Задача
мотора – равномерно с заданной скоростью прокачивать жидкость через активную
камеру. В активной камере, также герметично закрытой, происходят различные
биохимические реакции, однако время их возникновения и длительность протекания
различные. Скорость вытекания жидкости определяет мотор с насосом. Часть
питательной жидкости из активной камеры возвращается обратно в резервуар по
другой гибкой трубке. Это позволяет рационально расходовать весь имеющийся
объём резервуара. Таким образом, мы имеем замкнутую систему резервуар-активная
камера-резервуар.
Особенностью жидкости
является её химический состав. Было замечено, что с течением времени жидкость
постепенно высыхает и тем самым объём её в резервуаре может самопроизвольно
уменьшаться. Внутри резервуара находятся ряд датчиков уровня, температуры и
давления. В процессе работы замкнутой системы соблюдаются внешние и внутренние
параметры среды. Для ряда опытов применялся процесс насыщения питательной
жидкости кислородом и смешивание для исключения возможного загустевания. В процессе
исследования первоначальный объём жидкости не изменяют. Резервуар помещается в
закрытую камеру для защиты от внешних воздействий среды.

Рисунок 2 – Лабораторная установка
Датчики, измеряющие
изменения объёма потребляемой жидкости находятся и в активной камере.
Полученные значения соотносятся с данными датчиков из резервуара. Резервуар
имеет прозрачные стенки, что позволяет визуально оценить состояние качества
оставшейся питательной жидкости и текущий объём – рисунок 3.
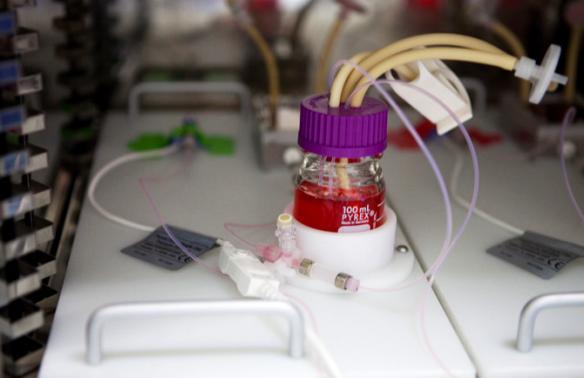
Рисунок 3 – Резервуар
Рассмотрим далее
математическую модель резервуара – рисунок 4. Модель блока Reservoir выполнена
в редакторе Simulink системы компьютерной
математики Matlab&Simulink R2013b. Представляемый
блок наиболее близко описывает поведение реального объекта и включает набор
всех элементов входящих в обеспечение данного блока в реальных условиях:
систему смешивания, датчики уровня, систему нагрева и др.
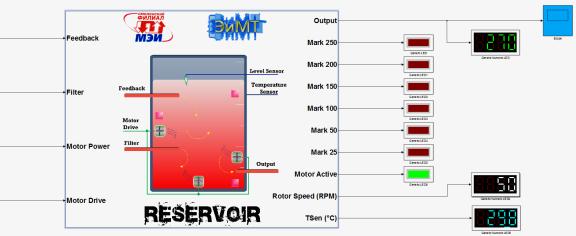
Рисунок 4 – Математическая модель резервуара
В
модели резервуара (см. рисунок 5 – структурная схема), оператором задаются параметры
условий среды, в которых происходит исследуемый процесс: температура жидкости,
давление, первоначальный объём, текущий уровень жидкости, критический уровень.
Процесс управления и обработки данных происходит при помощи модели микроконтроллера
(в реальных условиях при помощи цифровой системы управления).
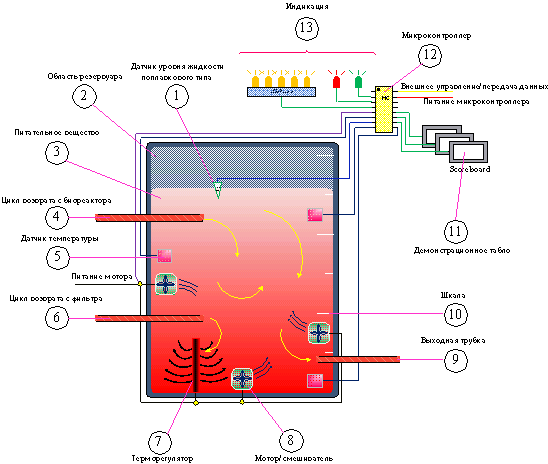
Рисунок 5 – Структурная схема модели
Далее следует описание
проводимых опытов. Исследования одновременно проводятся на математической
модели и в лаборатории (с целью отладки математической модели и составления
подробного описания реальных изменений наблюдаемого объекта).
Опыт 1. В резервуаре
находится 300 мл жидкости. Наблюдается процесс выливания с установленной
скорость жидкости из резервуара. Через трубку из активной камеры жидкость обратно
не возвращается в резервуар. Результат наблюдения и в реальном процессе и по математической
модели совпадает. Скачкообразные составляющие – процесс высыхания жидкости и её
перемешивание в резервуаре для поддержания первоначальной структуры. В первом
опыте в активной камере не формируются условия для возникновения биохимических
реакций. Как и следовательно, процесс вытекания имеет вид равномерно убывающей
кривой – рисунок 6. Результат опыта – жидкость в объёме 300 мл из резервуара без
системы возврата и при отсутствии биохимических процессов выливается примерно
через 250 часов.
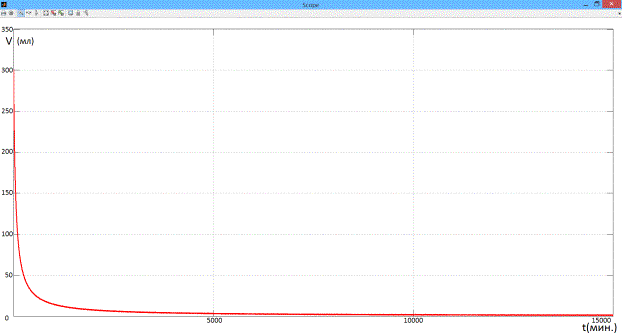
Рисунок 6 – Результат моделирования первого
опыта
Опыт 2. В резервуаре находится 200 мл жидкости. Наблюдается процесс
выливания с установленной скорость жидкости из резервуара. Через трубку из
активной камеры жидкость обратно возвращается в резервуар. В активной камере
моделируются биохимические реакции. Процесс смешивания или обогащения
кислородом в резервуаре отсутствует. Первичные результаты формируются при
оценке работы лабораторного стенда. Результаты моделирования и оценка
результатов лабораторного стенда совпадают. Идеализированный график представлен
на рисунке 7. Результат опыта – жидкость в объёме 200 мл из резервуара с
системой возврата и при наличии биохимических процессов выливается примерно
через 45 000 часов. Реальное наблюдение проводилось в течении пяти месяцев и позволило
сформировать базовые функции для описания изменений в активной камере.
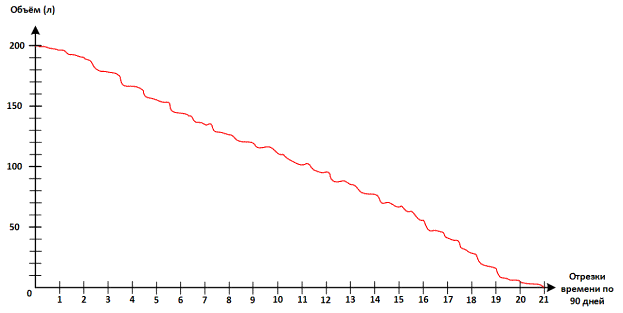
Рисунок 7 – Результат моделирования второго
опыта
При проведении второго опыта
были учтены важные особенности. В частности, температура среды менялась,
смешивание жидкости не проводилось. Процесс вытекания в течении всего времени
носит неравномерный вид.
Опыт 3. В резервуаре
находится 200 мл жидкости. Наблюдается процесс выливания с установленной
скорость жидкости из резервуара. Через трубку из активной камеры жидкость
обратно возвращается в резервуар. В активной камере моделируются биохимические
реакции. Процесс смешивания или обогащения кислородом в резервуаре
присутствует. Исследование проводится только путём математического
моделирования. Параметры объекта и среды соблюдаются согласно установленным требованиям.
Результат опыта – жидкость в объёме 200 мл из резервуара с системой возврата и
при наличии биохимических процессов выливается примерно через 48 000 часов.
Реальное наблюдение проводилось в течении трёх месяцев и позволило сформировать
базовые функции для описания более точных изменений в активной камере.
Идеализированный график представлен на рисунке 8.
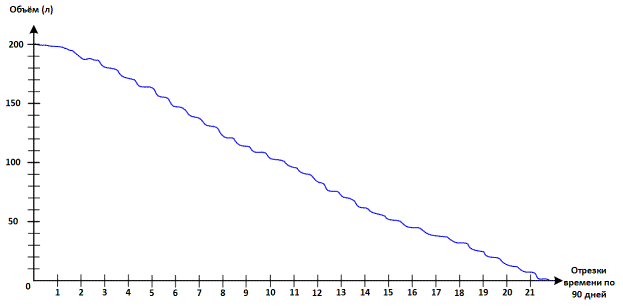
Рисунок 8 – Результат
моделирования третьего опыта
Анализ
рисунка 7 и 8 позволяет выявить наличие различных периодов потребления жидкости
активной камерой: старт, начало биохимических процессов, период активности,
период простоя – рисунок 9. Однако, следует заметить, что явной картины
наблюдения в тот или иной отрезок времени начала биохимических процессов и
возникновение периода активности не имеется. Поскольку реальные биофизические
процессы отличаются от математической модели как различной интенсивностью так и
дополнительными особенностями (чаще не повторяется по одному сценарию развития,
нежели математическая модель), то следует проводить грубое математическое
округление до некого периода времени, когда показатели модели и результаты
процессов в камере реального объекта будут схожи. Как было замечено, возможным
периодом наблюдения, взятого за единицу времени может быть декада = 90-92 дня.
Особенности прогнозирования обособлены особенностями активной камеры и формируемыми
процессами биологического характера.
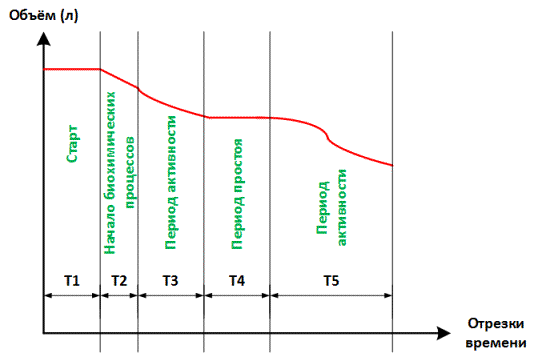
Рисунок 9 – Характер изменения потребления
жидкости с течением времени
В тоже время, можно
предположить, что период активности и период простоя (замедления процессов)
может иметь схожий графический вид – активность-замедление-активность. Это
объясняется невозможностью живых организмов непрерывно иметь процесс роста.
Согласно математическим вычислениям, на основе которых проектировалась модель
активной камеры, период активности будет сопоставляться с процессом роста и
иметь равноускоренный во времени характер изменений того и другого. Указанные
сведения позволяют более глубоко дать представление об исследуемых процессах, необходимых
статисту. Наличие ряда внешних факторов должно быть учтено в процессе
вычисления.
Для составления статистических
расчётов и проведения оценки изменения объёма жидкости в резервуаре следует ввести
следующие переменные:
► первоначальный объём
(Vs, мл) – является базовым элементов статистических расчётов. Прогноз может
быть составлен только при известном первоначальном объёме и соотносится с ним;
► период измерений (Z, дней)
– количество дней, выбранных за единицу оценки времени. Поскольку наблюдаемый
процесс вытекания продолжителен, в качестве периода были выбраны отрезки
времени 30 или 90 дней;
► скорость
вытекания жидкости из резервуара (M, мл/д) – определяющий
фактор движения жидкости через активную камеру. Первоначальная скорость в
процессе исследования должна быть неизменна. Данная величина создаётся
процессом выкачивания жидкости микромотором из резервуара в активную камеру (скорость
жидкости возвращаемой в резервуар из камеры обратно не учитывается);
► естественные
потери жидкости (H, мл/д) – скорость изменения объёма жидкости,
связанная с её высыханием и старением. Определяющим фактором является наличие
процесса смешивания в резервуаре и соблюдение температурных и атмосферных
условий среды;
► период активности
(Z1, дней) – отрезок времени в течении которого в
активной камере наблюдается процесс протекания биохимических реакций.
► период простоя
(Z2, дней) – отрезок времени в течении которого в
активной камере отсутствуют какие-либо изменения (следует заметить, что период
измерений Z=Z1+Z2);
Далее проводится уточнение
показателей изменения объёма жидкости при различном характере протекания
биохимических процессов в активной камере. Расчёт данных величин возможно
провести только по оценке жидкости, возвращаемой в резервуар:
▰ А – предполагаемый объём
жидкости, возвращаемой в резервуар в первый период измерений (как правило
соответствует состоянию старта и наполнению жидкостью всех узлов активной
камеры и микромотора);
▰ B – предполагаемый
объём жидкости, возвращаемой в резервуар во второй период измерений (как
правило соответствует состоянию проявления биохимических процессов);
▰ С – предполагаемый объём
жидкости, возвращаемой в резервуар во третий и последующий периоды измерений.
С=С1+С2, где С1 – объём жидкости потребляемый
в период активности (Z1 дней), С2 –
объём жидкости потребляемый в период простоя (Z2 дней).
На основании данных из ряда
опытов можно составить выражения, учитывающие изменения жидкости.
Потери жидкости в резервуаре
в первый период измерений (старт процесса):
![]()
Соответственно во второй
период измерений (активация биохимических процессов):
![]()
Учёт потерей жидкости в
третий и последующие месяцы имеет вид:
![]()
Вводится величина n – количество
последующих циклов измерений по Z дней, начиная с третьего
периода. Данное значение можно выразить из выражения:
![]() откуда получим:
откуда получим:
![]()
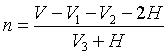
Задавшись постоянным
значением V, Z, M, H и установив предполагаемые
величины A, B, C можно определить количество
дней в течении которых будет израсходован первоначально известный объём
жидкости:
![]()
Математический расчёт был
подтверждён путём моделирования в среде Simulink системы компьютерной
математики Matlab&Similink R2013b. Базовая
схема измерений представлена на рисунке 10. Выбор системы Simulink для
проведения расчётов объясняется возможностью совмещения полученной схемы с
базовым блоком Reservoir, использованного при моделировании процессов всех
опытов. Совмещённая схема позволит одновременно проводить расчёт жидкости и
исследовать характер его изменения.
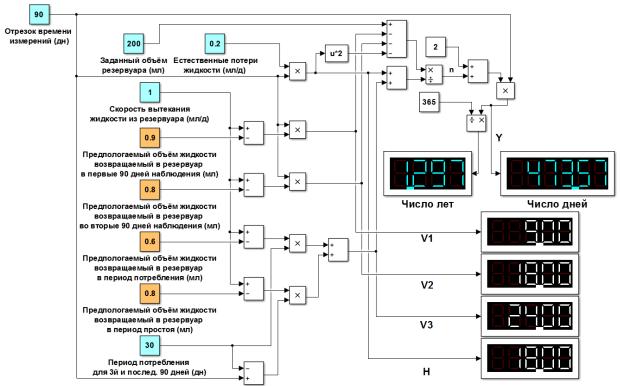
Рисунок 10 – Результаты
моделирования прогноза и оценки времени,
необходимого для вытекания жидкости из резервуара
На рисунке приведён процесс
оценки при первоначальном объёме жидкости в резервуаре 200 мл. Период времени
выбран 90 дней. При учёте остальных значений и процесса естественного
вытекания, результат моделирования: жидкость закончится за 473 дня ≈ 1,3
года. Соответственно, при прочих равных условиях, но с более интенсивной
скоростью подачи и при первоначальном объёме 300 мл, прогноз будет 218 дней –
рисунок 11.
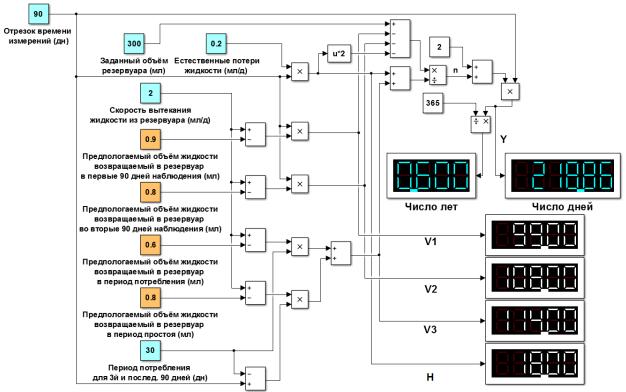
Рисунок 11 – Результаты
моделирования прогноза и оценки времени,
необходимого для вытекания жидкости из резервуара
Для более удобного
управления и ввода данных был сформирован субблок Simulink – рисунки 12-13.

Рисунок 12 – Панель ввода данных субблока

Рисунок 13 – Субблок системы Simulink
Полученная модель отражает
предварительный результат прогнозирования остатка питательной жидкости в
резервуаре. СА позволил обработать массив данных, выявить закономерности и в
упрощённой форме представить результат.
Разработанный блок,
выполняющий ряд простейших математических операций можно усложнять, задавая новые
условия. В частности, определить минимальный уровень по достижении которого
через выходную трубку не сможет поступать жидкость; провести измерения для
разных составов жидкости и указывать свойства среды при анализе, провести
исследование в режиме реального времени, совместив разработанный блок с моделью
активной камеры и др. Предложенные идеи являются основой дальнейших исследований
и материалом для проведения СА.
SOLUTION OF THE PROBLEM OF
ESTIMATION FLOW RATE IN THE TECHNOLOGICAL PROCESS
Delegovskaya T.V., Naydyonov E.V.
This paper describes the process of assessing
and predicting the feed liquid into techno-logical process of providing for
specific environmental conditions. Set of statistics can provide recommendations
for future use.
Key words: analysis, data, liquid, statistics, formula
ГБОУ ВПО «Смоленский Государственный Университет»
Филиал ФГБОУВПО
«Национальный исследовательский университет» МЭИ»
в г. Смоленске
Поступила в редакцию 27.11.2013