УДК 51

ПЕРВОЕ ЗНАКОМСТВО С СЕТЯМИ ПЕТРИ

ЧАСТЬ 2

ОСНОВЫ СЕТЕЙ ПЕТРИ

Рассматриваются возможности использования сетей Петри для исследования проблем медицинской морфологии. Даются основные понятия и представление о методах построения моделей.

Вторая работа данного цикла посвящена основным понятий и задачам, решаемых в рамках одной из разновидностей графов специального вида - т.н. сетей Петри. Дается представление о возможностях и ограничениях использования данного математического инструмента в медицинской морфологии.

Основные понятия

Графы специального вида, получившие в дальнейшем название “Сети Петри” были впервые введены Карлом Петри в 60-х годах. В следующем десятилетии начался “бум” разработок в этом направлении. В настоящее время поисковые машины Интернет дают несколько десятков тысяч ссылок на использование этого термина.

Популярность сетей Петри вызвана, на мой взгляд, удачным представлением различных типов объектов, присутствующих во многих моделируемых системах и “событийным” подходом к моделированию. Прекрасное изложение теории сетей Петри можно найти на русском языке в [1] и [2]. Формальное определение сетей Петри будет приведено ниже. Здесь же дать простое представление об этом математическом инструменте.

Сеть Петри определяется как двудольный граф. Т.е. все вершины графа относятся к одному из двух классов - позициям и переходам. Позиции изображаются окружностями, переходы - отрезками прямой. Дуги в сетях Петри - направленные. Причем каждая дуга связывает вершины только разных классов.

Либо начало дуги совпадает с позицией и тогда конец этой дуги совпадает с переходом, либо наоборот.

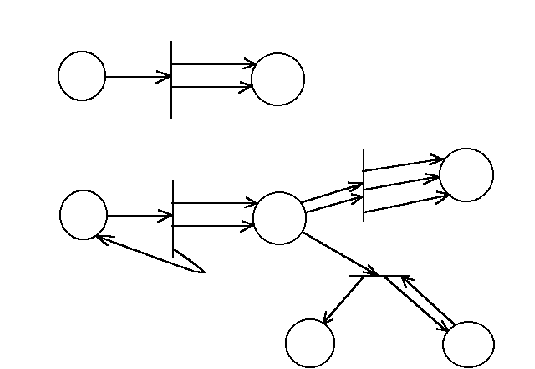
На рис.1 приведены примеры, соответствующие этому ограничению, на рис.2 - недопустимые примеры.

Рис.1

Рис.2

Оригинальным понятием теории сетей Петри является понятие “фишка”. Фишки изображаются точками, расположенными внутри позиций. Таким образом, каждой позиции сети ставится в соответствие натуральное число, указывающее количество фишек в данной позиция. Это число называют разметкой позиции, а совокупность таких чисел для всех позиций сети называют разметкой сети. Замечу, что позиция может и не содержать фишек, т.е. иметь нулевую разметку.

Пример сети с разметкой приведен на рис.3.

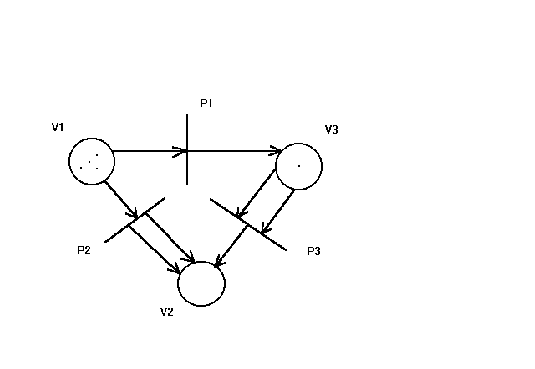
Рис.3

Другое оригинальное понятие сети Петри - “срабатывание” переходов.

Назовем входными позициями некоторого конкретного перехода - те позиции, из которых исходят дуги, входящие в данный переход. Соответственно, выходными позициями назовем позиции, в которые входят дуги, исходящие из данного перехода.

Например, на рис.3 для перехода P1 входная позиция V1- выходная -V3.

Срабатывание перехода состоит в изъятии фишек из каждой входной позиции и помещении их в каждую выходную позицию. Причем, количество фишек, изымаемых из конкретной позиции, или помещаемых в конкретную позицию равно количеству дуг, соединяющих срабатывающий переход с данной конкретной позицией.

Например, переход P1 на рис.3 при срабатывании изымает из позиции V1 одну фишку и увеличивает количество фишек в позиции V3 на одну.

Переход P2 изымает одну фишку из позиции V1 и помещает в позицию V2 две фишки.

Теперь естественно вводится условие срабатывания перехода. Переход срабатывает, если количество фишек в каждой входной позиции перехода не меньше количества дуг, соединяющих эту позицию с переходом.

Например, на рис.3. переход P3 не может сработать, ибо в позиции V3 находится только одна фишка, а дуг, связывающих V3 и P3 - две.

Как только введено понятие “срабатывание” перехода - появляется возможность говорить о функционировании сети и моделировании процессов, этапы которых связаны между собой причинно-следственной связью.

В самом деле, на рис.3 изображена сеть, в которой переход P3 не может сработать. Но если сработает переход P1, то количество фишек в позиции V3 - увеличится. Теперь P3 - сработает.

Разметку сети до срабатывания любого перехода называют начальной или стартовой разметкой. Затем срабатывает тот или иной переход. При этом разметка сети меняется. Возможно, что в результате этого изменения некоторый переход потеряет возможность срабатывать, или наоборот - приобретет ее. Последовательное срабатывание переходов и соответствующее изменение разметки сети называют процессом функционирования сети.

Завершение процесса функционирования приводит сеть к разметке, называемой конечной.

Собственно говоря, предметом теоретического исследования сетей Петри и является процесс их функционирования, т.е. возможные последовательности срабатывания переходов и свойства получаемых при этом разметок сети. И, как обычно в математике, такие исследования формулируются, как правило, в виде утверждений двух основных типов - утверждение о существовании и утверждения об обязательности.

Конечные разметки сети

Одна из основных проблем в теории сетей Петри - задача о конечности функционирования сети (о достижении тупиковой разметки, “смертельные объятия” и т.д.).

Суть проблемы состоит в ответе на вопрос для данной конкретной сети - существует ли такая последовательность срабатывания переходов, которая приводит сеть к тупиковой разметке (т.е. разметке, при которой ни один переход не может сработать)?

Если обратиться к рис.3 - очевидно, что последовательность P2,P2,P2,P2 (т.е. четыре подряд срабатывания перехода P2) делают дальнейшее срабатывание любого перехода в данной сети - невозможным. Желающие могут найти и другие последовательности срабатывания переходов, приводящих к такому результату.

Более того, анализ сети позволяет утверждать, что эта сеть всегда приходит к тупиковой разметке. Это математическое утверждение (теорема!) может быть строго доказано.

Заметим, что хотя рассматриваемая сеть обязательно останавливается, т.е. достигает тупиковой разметки, но сами эти тупиковые разметки могут быть различны.

Например, утверждение: “ сеть на рис.3 всегда останавливается, когда все фишки собраны в позиции V2” - справедливо.

А похожее утверждение: “ сеть на рис.3 всегда останавливается, причем все фишки собраны в позиции V2” - не верно.

Свойство достижения конечной разметки присуще далеко не всем сетям. Например, на рис.4 приведен пример сети всегда приходящей к тупиковой разметке, на рис.5 - сеть никогда не “попадает в тупик”, на рис. 6 - сеть, которая может остановиться, а может и нет.

Ограниченность

Другое направление исследования функционирования сети Петри связано с изменением количества фишек в конкретной или произвольной позиции в процессе функционирования сети.

Под ограниченностью понимают свойство сети не допускать превышения количества фишек в конкретной или произвольной позиции некоторого фиксированного числа.

Если ни в одной позиции сети при любой последовательности срабатываний переходов количество фишек не превышает некоторого K, то такую сеть называют K-ограниченной.

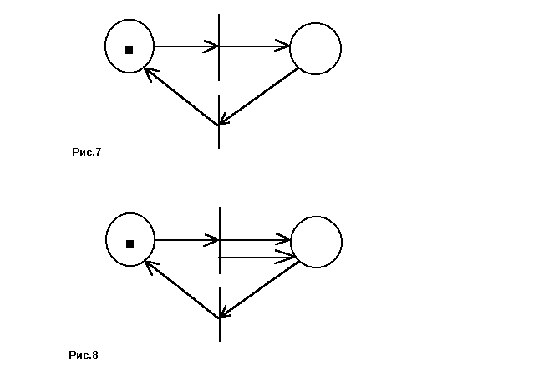
Например, сеть на рис.7 является ограниченной - при любом срабатывании сети количество фишек в любой позиции не превысит 1. Заметим, что само функционирование этой сети - бесконечно. Т.е. у данной сети отсутствует тупиковая разметка.

Так же не достигается тупиковая разметка сети на рис.8. Однако эта сеть не является ограниченной - количество фишек в любой позиции может увеличиваться бесконечно.

Другое свойство сети - безопасность.

Моделирование с помощью сетей Петри

В первой статье этого цикла говорилось о двух основных подходах к моделированию объектов графами - “географическом” (граф соответствует структуре моделируемого объекта) и “состоятельном” (граф соответствует процессам, т.е. изменению состояний объекта).

Представим себе сеть Петри, изображающую структуру человеческого организма, где позиции соответствуют органам, дуги (с переходами) - кровеносным сосудам, фишки - некоторому стандартному объему крови. Если такая сеть не является ограниченной, то количество фишек в какой-либо позиции (и, соответственно, количество и давление крови в этом органе может возрастать) неограниченно. Что, естественно, соответствует кровоизлиянию.

Сети Петри, позволяя использовать такой подход, чаще применяются для моделирования процессов.

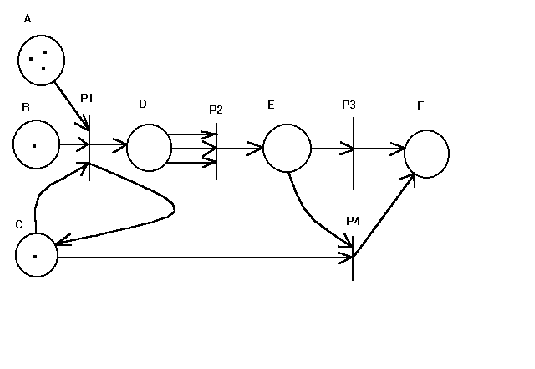
Например, на рис.9 изображена сеть, моделирующая известный эксперимент по выработке условного рефлекса слюноотделения у собаки как реакции на электрический звонок.

Рассмотрим данную сеть подробнее. Здесь позиции именуются буквами латинского алфавита: переходы - буквой P с номером. Позиция A соответствует множеству порций пищи, используемой в эксперименте, причем каждая порция изображается одной фишкой, размещаемой в данной позиции. Позиция B соответствует экспериментатору, а фишка в этой позиции изображает его готовность приступить к эксперименту. Позиция C представляет электрический звонок, а фишка в этой позиции - способность звонка звонить.

Сразу же видно различие в стартовой разметке

ЛИТЕРАТУРА

1. Котов В. Е. Сети Петри. - М.: Наука, 1984.

2. Питерсон Дж. Теория сетей Петри и моделирование систем. - М.: Мир, 1984.

3. Майника Э. Алгоритмы оптимизации на сетях и графах /Под ред. Е.К.Масловского - М.: Мир,1981. - 322 c.

Смоленский гуманитарный университет

Финляндия

Поступила в редакцию 31.01.99.