УДК 51

ОСНОВЫ МОДЕЛИРОВАНИЯ СЕТЯМИ ПЕТРИ СИСТЕМ С ПАРАЛЛЕЛИЗМОМ

© 1998 г. Н.С. Писаренкова

Рассматриваются особенности моделирования систем с параллелизмом. Вводится понятие условно-событийной системы и рассматривается интерпретация ее элементов элементами сети Петри. Дается определения сети Петри и ее работы. Обсуждаются примеры синтеза сетевых моделей.

Биологические и технические системы, исследованием и конструированием которых занимается человек, различаются физическими свойствами, функциональным назначением, сложностью внутренней структуры. Так, организм человека можно представить как совокупность множества органов и происходящих в них процессов. Функции органов и содержание процессов существенно различаются. При этом процессы, протекающие в отдельных органах (или тканях), оказываются взаимосвязанными, взаимодействующими друг с другом в некоторые моменты времени. В технике все большее распространение получают параллельные системы с недетерминированным поведением, в которых отдельные компоненты функционируют параллельно и взаимодействуют асинхронно. Примерами таких систем могут служить многопроцессорные вычислительные машины, автоматизированные системы управления, параллельные программы и так далее.

Основным методом исследования сложных систем стало математическое моделирование. Процесс построения модели состоит из нескольких этапов. На первом этапе моделирования происходит формирование абстрактных логических представлений об объекте путем выделения наиболее существенных его свойств и признаков, представления этих свойств в упрощенной форме, а также поиск подходящего математического аппарата для формального описания и исследования свойств модели.

Взаимоотношения между объектом, моделью и математическим аппаратом в графическом виде можно представить, как это изображено на рисунке 1. Модель представляет собой срез (сечение), вид, размеры и форма которого зависят от места сечения (или задач моделирования) и применяемого инструмента (математического аппарата). На разных этапах исследования могут формироваться различные модели.

Рис. 1. Размеры сечения определяются местом его расположения.

Для того, чтобы выбрать адекватный математический аппарат, предназначенный для моделирования некоторого класса систем, необходимо установить круг вопросов, которые должны решаться с помощью моделей.

В системах с параллелизмом на первый план выдвигаются вопросы "качественного" характера: как взаимодействуют отдельные компоненты системы; имеются ли в системе потенциально "узкие" места; могут ли в системе возникнуть нарушения функционирования, сбои и как можно их локализовать; можно ли упростить систему, заменив ее отдельные компоненты; может ли система выполнять те функции, для которых предназначена. То есть исследователя в первую очередь интересуют структурные характеристики и свойства.

В таких случаях модель системы должна быть структурно подобна самой системе. Это означает, что модель можно строить по частям, как и систему. Глобальные функции и понятия могут определяться на основе локальных, соответствующих компонентам, подсистемам и подпроцессам; связи и отношения между фрагментами модели подобны связям и отношениям между фрагментами системы.

В настоящей статье формулируются основные принципы сетевого подхода к моделированию систем с параллелизмом и вводятся базовые понятия теории сетей Петри.

Условия, события, процессы.

Основой сети Петри является понятие условно-событийной системы. Компоненты системы и их действия представляются абстрактными событиями . Примерами событий могут быть: выпaдение осадков, открытие венозного клапана, наличие воспалительного процесса, переключение триггера, прохождение этапа пути или проекта и так далее.

Событие может произойти (реализоваться) один раз, повториться многократно или не произойти ни разу. Например, венозный клапан может открываться и закрываться многократно, но может в результате тромбоза оказаться закупоренным. В условно-событийной системе это будет означать, что событие является заблокированным и не может быть реализовано до тех пор, пока не произойдет либо вымывание тромба, либо удаление его в результате оперативной хирургической помощи.

Совокупность действий, возникающих как реализация событий при функционировании системы, образует процесс , порождаемый этой системой. В общем случае одна и та же система может функционировать в одних и тех же условиях по-разному, порождая некоторое множество процессов.

Для того, чтобы событие произошло, необходимо появление ситуации, в которой это событие может быть реализовано. При этом ситуация определяется как совокупность некоторых условий возникновения события. То есть событие реализуется, если выполнены условия его реализации. Условие может иметь емкость: условие не выполнено (емкость равна нулю), условие выполнено (емкость равна единице), условие выполнено с n-кратным запасом (емкость равна n, где n - целое положительное число). Например, условием выпадения осадков является наличие облачности на небе (понятно, что одного этого условия недостаточно, поэтому исследователь должен сформулировать некоторый набор условий выпадения осадков при моделировании атмосферных явлений). Еще примеры: чтобы венозный клапан оказался закупоренным, необходимо наличие тромба; воспалительный процесс в тканях начинается при условии попадания туда патогенного микроорганизма; переключение триггера возможно, если входной сигнал имеет достаточный уровень.

В результате совершения события происходит изменение условий и наступление постусловий реализации события. Так, результатом выпадения осадков может стать появление радуги, из-за закупорки венозного клапана может появиться отек конечности, а последствием срабатывания триггера может оказаться включение сигнала тревоги.

Сети Петри: основные понятия

В первой статье этого цикла читатели познакомились с основами теории графов, а также с принципами построения и исследования моделей на графах. Сети Петри представляют собой двудольный ориентированный граф, в котором имеются вершины двух типов: вершины одного типа называются местами, а вершины другого типа - переходами. Для условно-событийных систем места сети Петри интерпретируются как условия (предусловия, постусловия совершения события), а переходы соответствуют событиям, происходящим в системе.

Элементарная сеть Петри изображена на рис. 2.

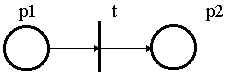
Рис. 2. Элементарная сеть.

В графическом представлении сетей переходы изображаются "барьерами", а места - кружками. Условия-места и события-переходы связаны отношением непосредственной зависимости, которое изображается с помощью направленных дуг, ведущих из мест в переходы и из переходов в места. Места, из которых выходят дуги, направленные к данному переходу, называются его входными местами. Места, в которые входят дуги, исходящие из данного перехода, называются его выходными местами. Так, в элементарной сети на рис.2 место p1 является входным для перехода t , а место p2 - выходным.

Динамика поведения моделируемой системы (и в этом принципиальное отличие сетей Петри от графовых моделей, которые по своей сути являются статическими) находит свое отражение в функционировании (работе) сети Петри. Неформально работу сети можно представить как совокупность срабатываний переходов. Переход может сработать, если выполнены все условия реализации соответствующего события. Выполнение условия в сетях Петри отображается разметкой соответствующего места, то есть размещением в нем одного или нескольких маркеров (фишек) в соответствии с емкостью условия. В графическом представлении маркер обозначается точкой внутри соответствующего места. Так, если в место p1 на рис.2 поместить маркер, то это будет означать, что условие совершения события t имеет место (выполнено) и событие может произойти (рис. 3.а).

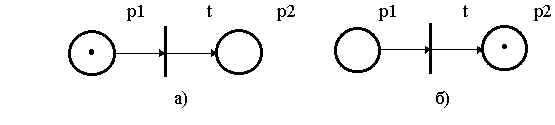
Рис. 3. Срабатывание перехода в элементарной сети.

Срабатывание перехода - неделимое действие, изменяющее разметку его входных и выходных мест следующим образом: из каждого входного места маркер изымается, а в каждое входное место - добавляется. Тем самым реализация события изменяет состояние непосредственно связанных с ним условий: предусловия возникновения события перестают существовать, зато возникают постусловия совершения события. Для элементарной сети на рис. 3 факт срабатывания разрешенного перехода t отмечается изменением маркировки: маркер, находившийся в месте p1 в результате срабатывания перехода перемещается в место p2 (рис. 3,б). В общем виде, когда переход связан со своими местами не ординарными, а кратными дугами, правило срабатывания перехода звучит так: при срабатывании перехода t он изымает из каждого своего входного места столько маркеров, какова кратность дуги, связывающей этот переход с указанным местом, и добавляет в каждое свое выходное место количество маркеров, равное кратности связывающих их дуг.

Это правило иллюстрирует рисунок 4. На нем переход t имеет два входных и одно выходное место, причем входное место p1 содержит два маркера, а входное место p2 - пять маркеров. Место p1 связывает с переходом t ординарная дуга, а место p2 - дуга, кратность которой равна трем. Очевидно, что переход t может сработать, так как количество маркеров в его входных местах больше кратности дуг, связывающих эти места с переходом. При срабатывании t из места p1 будет извлечен один маркер, а из места p2 - три маркера. Выходное место p3 связано с переходом t дугой с кратностью 2, поэтому результатом срабатывания перехода будет помещение в p3 двух маркеров (рис. 4б). Таким образом, в результате срабатывания перехода t маркировка мест сети изменится и будет следующей: в p1 содержится один маркер, в p2 - два маркера и в p3 - тоже два маркера. Необходимо отметить, что переход t при такой разметке не может сработать еще раз: количество маркеров в p2 меньше, чем кратность связывающей это место и переход дуги. Переход будет запрещен до тех пор, пока в место p2 не добавится хотя бы один маркер.

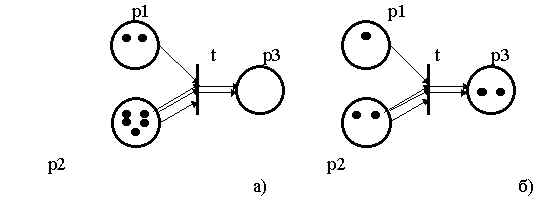
Рис. 4. Иллюстрация к правилу срабатывания перехода

Формальное определение сети Петри

Существует несколько формальных определений сети Петри, отличающихся способами задания элементов и связей в сети. В этой статье автор будет придерживаться обозначений и определений, используемых В.Е. Котовым в его известной монографии [1].

Под сетью будем понимать тройку (P, T, F), где

P - непустое множество элементов сети, называемых местами;

T - непустое множество элементов сети, называемых переходами;

F - функция инцидентности, задающая связи между элементами множеств P и T, и для (P, T, F) выполнены следующие условия:

1. P T = (множества мест и переходов не пересекаются);

2. (F ) ( x P T, y P T: xFy yFx ) (то есть любой элемент сети инцидентен хотя бы одному элементу другого типа);

3. Если для произвольного элемента сети x X обозначить через *x множество его входных элементов, а через x* - множество его выходных элементов, то

p1, p2 P: (*p1 = *p2) (p1* = p2*) (p1 = p2),

(то есть сеть не содержит пары мест, которые инцидентны одному и тому же множеству переходов).

На основе понятия сети, которая описывает только статическую топологию моделируемого процесса или системы, вводятся динамические сетевые структуры, в которых местам приписываются специальные разметки, моделирующие выполнение условия, и с сетью связывают понятие ее функционирования, изменяющего эти разметки (условия) в результате срабатываний переходов. К таким динамическим сетям относятся сети Петри, их различные варианты, обобщения и частные случаи.

Сеть Петри - это набор PN = (P, T, F, M0), где (P, T, F) - конечная сеть (множества P и T конечны), а М0 - функция начальной разметка сети, которая сопоставляет любому месту pi P некоторое число M0(p)= n.

Функционирование сети Петри описывается формально с помощью множества последовательностей срабатываний и множества достижимых в сети разметок. Эти понятия определяются через правила срабатывания переходов сети.

Разметка сети PN является функцией M : P N (здесь N - множество натуральных чисел). Если предположить, что все места сети строго упорядочены каким-либо образом, т.е. P = ( p1, p2, ...pn), то разметку M сети (в том числе и начальную разметку) можно задать как вектор чисел M = (m1, m2,... mn) такой, что для любого i, 1 i n mi = M(pi). Если P' = {pi1, pi2, ...pik) - подмножество мест из P, то условимся через M(P') обозначать множество разметок {M(pi1),...M(pik)}. Если P' представить как вектор P' = (pi1, ... pik), то M(P') обозначает вектор проекции разметки M на P'.

Переход t может сработать при некоторой разметке M сети PN, если p*t M(p) F (p,t), то есть каждое входное место p перехода t имеет разметку, не меньшую, чем кратность дуги, соединяющей p и t. Это условие можно переписать в векторной форме следующим образом:

M *F (p,t).

Для ординарной сети Петри (то есть сети, в которой дуги имеют кратность, равную единице) условие срабатывания перехода означает, что любое входное место этого перехода содержит хотя бы один маркер, то есть имеет ненулевую разметку.

Срабатывание перехода t при разметке M порождает разметку M' по следующему правилу:

p P : M'(p) = M(p) - F (p,t) + F (t,p) , то есть

M' = M - *F(t) + F*(t).

На множестве разметок вводят отношение [ > непосредственного следования разметок:

M [ > M' t T : (M *F(t)) & (M' = M - *F(t) + F*(t)),

то есть разметка M' непосредственно следует за разметкой M, если найдется такой переход t, который может сработать при разметке M и разметка M' является результатом срабатывания этого перехода при разметке M.

Говорят, что разметка M' достижима от разметки M, если существует последовательность разметок M, M1, M2, ...M' и слово = t1t2......tk в алфавите T такие, что M[t1 > M1[t2> M2.....[tk> M'.

Слово в этом случае называется последовательностью срабатываний, ведущих от M к M'.

Множество разметок, достижимых в сети PN от разметки M, обозначим через R(PN,M). Множество R(PN) = R(PN,M0), то есть множество всех разметок, достижимых в сети PN от начальной разметки M0, называют множеством достижимых разметок сети. Свойства сети Петри определяют, исследуя возможные последовательности срабатываний переходов и множество достижимых в сети разметок. Обсуждению этих вопросов будет посвящена следующая статья нашего цикла.

Примеры синтеза сетевых моделей

Пример 1.

Рассмотрим, как можно отобразить сетью Петри процесс возникновения и развития инсульта (апоплексии). Как известно, причиной инсульта может быть либо закупорка сосуда головного мозга в результате развившегося тромбоза, либо разрыв стенки сосуда в результате атеросклеротических изменений в нем. При этом происходит развитие очага некроза или кровоизлияния с последующим поражением одного или нескольких центров головного мозга, которое и вызывает апоплексический удар. В результате паралича отдельных органов при отсутствии или недостаточности лечебных мероприятий может наступить смерть больного.

Выделим основные события рассмотренного процесса. При атеросклерозе это будут следующие события:

а.1 прорыв стенки сосуда;

а.2 развитие очага кровоизлияния;

а.3 поражение центра головного мозга;

а.4 апоплексический удар.

При тромбозе это будут события:

б.1 закупорка сосуда головного мозга;

б.2 развитие очага некроза;

б.3 поражение центра головного мозга;

б.4 апоплексический удар.

Каждому из событий ставится в соответствие переход сети Петри, имеющий соответствующий номер. Переходы последовательно связываются друг с другом входными/выходными местами. Очевидно, что события а.3, а.4 и б.3, б.4 являются идентичными. Это обстоятельство позволяет синтезировать единую сетевую модель, приведенную на рисунке 5. Указанная модель синтезирована из предположения, что условия возникновения событий всегда выполняются. В противном случае в модель необходимо вводить дополнительные места, соответствующие набору условий выполнения перечисленных событий

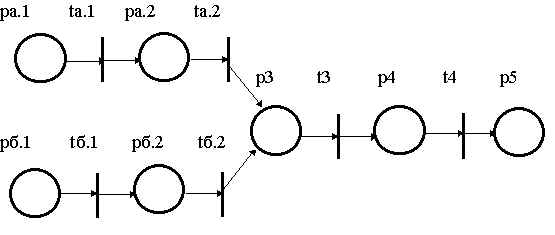
Рис. 5. Сетевая модель процесса возникновения инсульта

Начальное маркирование сети определяется характером заболевания. Если это тромбоз, то маркер будет помещен в место рб.1, а при атеросклерозе маркер необходимо поместить в место ра.1.

Пример 2.

Задача о пяти философах

Пять философов гуляют в саду и размышляют. Когда философ чувствует голод, он заходит в столовую, где стоит круглый стол с пятью стульями и миской спагетти посреди стола. На столе - пять вилок, по одной слева и справа от каждого стула (рис. 6). Философ берет вилки (если они на месте) и ест спагетти (для этого обязательно нужно две вилки: в левую и в правую руки). Утолив голод, философ кладет вилки на стол и выходит в сад размышлять, пока вновь не почувствует, что проголодался. Задача: требуется предложить такую модель, которая позволила бы синхронизировать независимые действия философов и не допускала взаимной блокировки, когда все философы сидят за столом, каждый из них взял по одной вилке и никто не может начать есть спагетти.

Представим набор действий всех философов матрицей PH размерностью 5x7, в которой i-я строка PH [i, ] соответствует действиям i-го философа. Каждый из философов выполняет 7 действий:

PH [i,] = PH [ i,1] - философ i входит в столовую;

PH[ i,2 ] - философ i берет левую вилку;

PH[ i,3 ] - философ i берет правую вилку;

PH[ i,4 ] - философ i ест спагетти;

PH[ i,5 ] - философ i кладет левую вилку;

PH[ i,6 ] - философ i кладет правую вилку;

PH[ i,7 ] - философ i выходит из столовой.

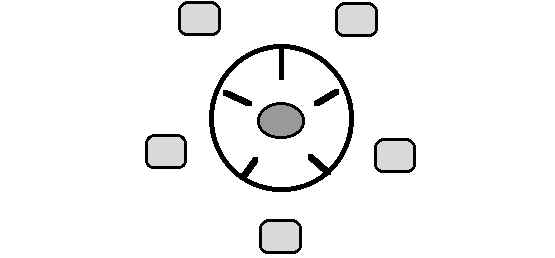
Рис. 6. Обеденный стол философов

Поведение отдельного философа можно промоделировать сетью Петри, изображенной на рисунке 7. Каждому действию i-го философа ставится в соответствие переход в сетевой модели, который имеет тот же номер, что и строка в матрице действий. Предполагается, что действия, связанные с вилками, философ может осуществлять независимо и одновременно. В модели факт параллельности действий отображается параллельными ветвями сети (переходы с номерами (i,2) и (i,3), а также (i,5) и (i,6) могут сработать независимо и одновременно). Для того, чтобы синхронизировать независимые действия философов, необходимо ввести в модель элементы, регламентирующие использование вилок двумя соседними философами. В качестве таких элементов можно использовать дополнительные места, имеющие единичную маркировку. Единственный маркер разрешает срабатывание только одного из разрешенных переходов (в том случае, если одновременно два философа сели на соседние места и претендуют на одну и ту же вилку. Этим в модели обеспечивается невозможность одновременного использования одной и той же вилки двумя обедающими философами.

Очевидно, что решением проблемы обеспечения отсутствия блокировок может стать запрет на одновременное присутствие в столовой более, чем четырех философов. В модели это решение обеспечивается ведением еще одного дополнительного места, количество маркеров в котором равно четырем. Это место связано входными дугами с первым переходом модели действий каждого из пяти философов. Когда философ входит в столовую, в модели это отображается появлением маркера во входном месте перехода t(i,1). Если в дополнительном месте имеется маркер, то обед будет разрешен, в противном случае (если в столовой уже обедают четыре человека) философ будет ждать, пока один из обедающих не освободит ему место.

Результирующая сеть показана на рисунке 9.

Таким образом, предложенная сетевая модель позволяет синхронизировать независимые действия философов и не допускает взаимной блокировки процессов.

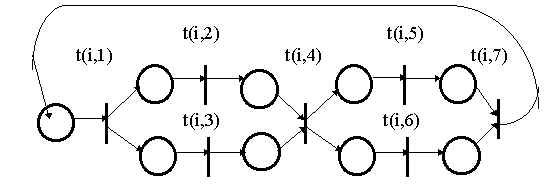
Рис. 7. Сетевая модель действий одного философа

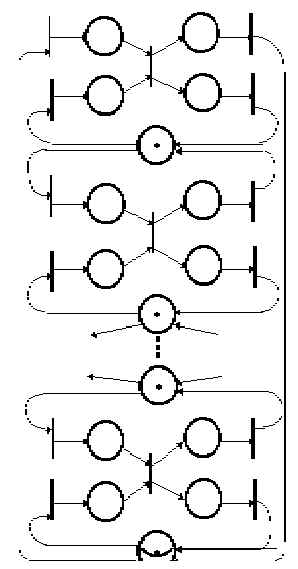
Рис. 8. Механизм синхронизации




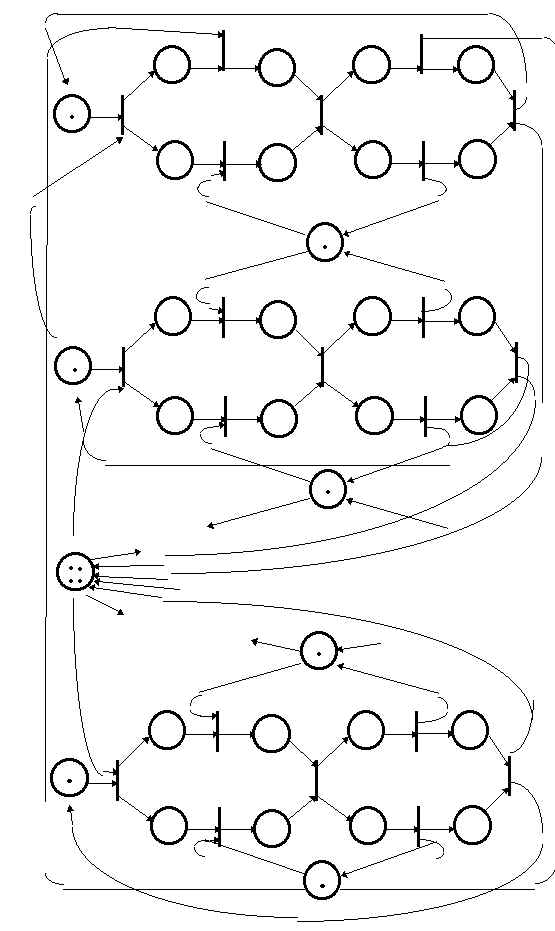
Рис. 9. Сетевая модель решения задачи о пяти философах

ЛИТЕРАТУРА

1. Котов В. Е. Сети Петри. - М.: Наука, 1984. - 160 с.

2. Писаренкова Н. С., Гарбуз Г. Г. Некоторые вопросы моделирования АСУ ПВО с применением аппарата сетей Петри /В сб. "Научные труды академии". Вып.2. - Смоленск: ВА ПВО СВ РФ, 1995.

Научно-исследовательский центр военной академии ПВО СВ РФ

Поступила в редакцию 21.05.98.