Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 12. -

Вып. 4. - 2013. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-40-html/TITL-40.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-40-html/cont.htm

УДК 004.021

ПРИМЕНЕНИЕ КОРРЕЛЯЦИИ В РОБОТОТЕХНИЧЕСКОМ ЗРЕНИИ: НАВИГАЦИЯ В ПРОСТРАНСТВЕ

Ó 2013 г. Киселев К. О.

(kiselev.doc)

В работе изложен способ определения положения робота в пространстве без применения для этого специальных маяков. Предлагаемый способ основан на использовании информации о расстоянии до объектов для определения собственного положения в помещении. На основе этого способа реализован алгоритм определения положения робота в помещении, план которого хранится в памяти.

Ключевые слова: компьютерное зрение, робототехника, навигация.

Для нормального функционирования роботов, способных самостоятельно передвигаться, необходимы методы определения текущего места расположения. Так решение задачи о перемещении в указанную точку становится невозможным, если отсутствует информация о том, где сейчас находится робот. Часто для определения положения применяется измерение расстояний, пройденных роботом и маяки (световые, звуковые или радио). При этом первый метод оказывается неработоспособен при частом перемещении из-за накапливающейся ошибки, а использование маяков требует предварительного оборудования помещения.

Предлагаемый способ заключается в применении дальномеров (ультразвуковых, лазерных или радиолокационных) для построения карты окружающего пространства. В дальнейшем эта карта сопоставляется с имеющейся картой помещения для получения текущего положения.

Исходными данными для работы являются: матрицаM - план помещения(размером M_a×N_a) и массив измерений дальномера.

Матрица плана помещения представляет собой двумерный массив точек, каждая из которых может иметь одно из 3-х значений:

a_c – свободное пространство

a_п – известные препятствия(стены, предметы мебели и пр.)

a_н – неисследованное пространство

Массив измерений дальномера представляет собой набор точек (l_i, α_i) – расстояния l_i до объекта в направлении угла α_i. При этом масштаб l_i должен совпадать с масштабом плана помещения. По этим данным строится матрица T образа помещения.

Необходимо иметь переменную α₀ – угол ориентации робота в помещении. При расчете положения обрабатываются несколько вариантов значения этого угла, если имеется информация о его предыдущем значении и максимально возможном изменении, либо перебираются все варианты от 0 до 360^о с шагом Δα. Рассмотрим второй случай, тогда α_0n=n*360/Δα, где n –целое число, такое, что 0a_0n<360^o.

Определяетсяl_max- максимальное из расстоянийl_i, округленное до целого числа вверх.Матрица T_n будет иметь размер M×N, где N=M=2*(l_max+2).

Зададим начало координат в точке (x₀, y₀) где x₀=y₀=l_max+2. Зададим каждому элементу матрицы значение a_н.

Зададим значениеa_сдля всех точек матрицы Т_n, лежащих на прямой между точками (x₀, y₀) и (x₀+l_i*cos(α_0n+a_i); y0+l_i*sin(α_0n+a_i)). Для точки (x₀+l_i*cos(α_0n+a_i); y0+l_i*sin(α_0n+a_i)) матрицы Т зададим значение а_п. Если известна погрешность измерения расстояния ±Δl, то имеет смысл заполнить значениями a_п ячейки между точками (x₀+(l_i-Δl)*cos(α_0n+a_i); y₀+(l_i-Δl)*sin(α_0n+a_i)) и (x₀+(l_i+Δl)*cos(α_0n+a_i); y₀+(l_i+Δl)*sin(α_0n+a_i)). При этом изначально следует принять значение l_max=max(l_i)+Δl.

В результате получим n матриц T_n. Вычислив ВКФ матрицы M с каждой из матриц T_n, получим n матриц C_n – коэффициентов корреляции матриц T_n и M при различных взаимоположениях. Исходя из свойств коэффициента корреляции известно, что он принимает максимальное значение, когда данные на входе идентичны. И чем меньше расстояние между векторами на входе, тем выше значение коэффициента корреляции. Учитывая выражение, определяющее значение C_n(k,p)[1]:

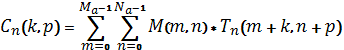
Составим требования к значениям констант а_с, а_н, а_п:

Если нет данных о какой-либо точке, то эта точка не должна воздействовать на значение C_n(k,p), поэтому:

а_н*а_с=а_н*а_п=а_н*а_н=0 (1)

Несовпадение значений в какой-либо точке должно приводить к снижению C_n(k,p), поэтому:

а_н*а_с<0 (2)

Совпадение значений в какой либо точке должно приводить к возрастанию C_n(k,p), поэтому:

а_н*а_н=а_с*а_с>0 (3)

Из условия (3) следует, что числа а_с, а_н, а_п – действительные, из условия (1) a_н=0, из условия (2) следует, что а_с, и а_п отличны от нуля и имеют противоположные знаки.

Набор матриц Сn можно представить как трехмерную матрицу С размером nx(M+M_a-1)x(N+N_a-1). Найдя максимум в этой матрице получим его координаты: (а_c, x_c, y_c).

a_c – информация о угле α₀ поворота робота в пространстве:

α₀=a_c*360/Δα

По x_c, y_c рассчитывают положение робота на карте по формулам:

x=x₀+M_a-x_c+1

y=y₀+N_a-y_c+1

Тогда робот находится в точке M(x,y) и установлен в направлении α₀. Эти координаты полностью описывают положение робота на плоскости, чего вполне достаточно для роботов, работающих внутри помещений.

Аналогичным образом возможно и определение координат в трехмерном пространстве. Входными данными при этом будет набор векторов (l_i,θ_i,φ_i) в трехмерной сферической системе координат, матрица M так же должна быть трехмерной.

При реализации алгоритма имеет смысл корректировать размер матриц T_n для увеличения быстродействия, т.к. если l_max значительно превосходит среднее расстояние до окружающих объектов, то значительная часть матрицы T_n останется заполненной a_н и не будет принимать участия в расчете, однако размер C_n и объем расчетов при этом окажется выше необходимого. Вычисление корреляции так же эффективнее реализуется не по определению, а при помощи двумерного БПФ[3].

Проиллюстрируем работу метода моделированием в Matlab.

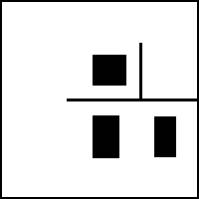
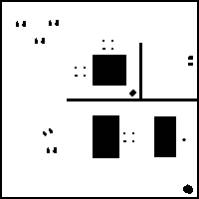
а б

Рисунок. 1 а - изображение карты тестового помещения, б - изображение карты тестового помещения для получения набора векторов (l_i, α_i).

На рис. 1 белым обозначены области, заполненные a_c, черным – a_п. Карта рис.1а будет использоваться для расчета, эта карта хранится в памяти робота, используется в качестве матрицы M. Карта на рис. 1б имитирует наличие необозначенных в памяти робота препятствий: стульев, ног людей, мусорных урн и т.п.

При моделировании робот помещается в тестовую точку с произвольными координатами(при условии, что точка свободна) и произвольным углом α₀, измеряется расстояние до предметов вокруг по карте рис. 1б с шагом 3,6^о. Расчет угла ведется с разрешением Δα=1^о(n=360). Так же на расстояние до предметов действует шум с нормальным распределением. Используется алгоритм с вычислением корреляции с помощью БПФ по оптимизированной карте. Размер матрицы M 200x200. Расчет производился для 10 случаев, при этом каждый раз робот устанавливался в новую точку, не связанную с предыдущим расчетом. Результаты представлены в табл. 1.

Таблица 1 – Результаты моделирования

№	α0, рад.	α0, рад. Вычисл.	Х	Х выч.	Y	Y выч.	Время расчета, с.	Ошибка α0, рад.	Ошибка X	Ошибка Y
1	1.8812	1.885	187	187	15	15	942	0.0038	0	0
2	0.5225	0.5236	30	30	175	175	575	0.0011	0	0
3	3.1297	3.1241	173	173	94	94	866	0.0056	0	0
4	1.0738	1.0821	69	69	58	58	844	0.0083	0	0
5	5.1389	5.1487	181	181	188	188	501	0.0098	0	0
6	3.4681	3.4732	167	167	103	102	503	0.0051	0	1
7	0.5715	0.576	162	162	93	93	780	0.0045	0	0
8	5.5558	5.5501	63	63	81	81	468	0.0057	0	0
9	2.1229	2.1293	30	30	171	171	599	0.0064	0	0
10	5.2929	5.2883	105	105	45	45	893	0.0046	0	0
Макс.							942	0.0098	0	1

Из результатов видим стабильную работу алгоритма. Погрешность расчета координат: ±1, максимальная ошибка измерения угла 0,0098 рад = 0,56^о, что меньше разрешения расчета. Главным недостатком алгоритма является его значительная вычислительная емкость: расчет одного тестового случая занимает до 16 минут на процессоре AMDAthlonx64 2.2 ГГц.

Для сокращения времени расчета эффективно уменьшение разрешения расчета угла или поиск угла из некоторого диапазона, определяемого внешними устройствами, например, электронным магнитометром, используемым в качестве компаса.

Для обеспечения работоспособности алгоритма единственным требованием к дальномеру является минимальный апертурный угол. Этому требованию соответствует применение лазерных дальномеров. УЗ дальномеры обычно имеют апетрурный угол шире 10^о, поэтому они сильно искажают данные измерений и не позволяют добиться высокой точности позиционирования без применения дополнительных мер.

Чувствительность алгоритма задается с помощью значений а_п и а_с. Корреляционный максимум имеет наиболее острый пик при а_п=-а_с. Однако такое сочетание параметров при обнаружении не отмеченных на карте объектов может приводить к ошибкам. Поэтому в некоторых случаях имеет смысл а_с задавать равныма_н, а а_п>0.

Так же в случае наличия на карте областей с одинаковым расположением препятствий, наличии какой-либо симметрии алгоритм оказывается не работоспособным без информации о предыдущем положении, т.к. возникает 2 и более корреляционных максимумов.

Разработанный метод позволяет получить информацию о положении робота на хранящейся в памяти карте, не имея предварительных данных о положении. Так же в процессе работы карта может дополняться и корректироваться, основываясь на показаниях дальномеров. Удачным вариантом применения алгоритма станет первоначальный расчет положения при включении робота, когда нет предварительных данных о его положении. Включение обычно производится в неподвижном состоянии, поэтому к сроку окончания расчета данные будут актуальны. Производительность может быть заметно увеличена применением технологий вычисления на GPU (Вычисление 8388608 отсчетов FFT:GPU: 0.085с, CPU: 92.851c[2]).

Литература

1. Гансалес Р., Вудс Р. Цифровая обработка изображений. М., Техносфера, 2005.1012 с.

2. Вычисление БПФ на GPU с использованием Java и CUDA, http://blog.eqlbin.ru/2011/08/gpu-java-cuda.html

3. Гансалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB. М., Техносфера, 2006. 615 с.

APPLICATION OF CORRELATION In Robotic Vision: NAVIGATING IN ROOM

Kiselev K. O.

The paper describes a method for determining position of the robot in the room without the use of a specialpoints. The proposed method is based on the use of information about the distances to objects for determine their own position in the room. Based on this method, implemented an algorithm determining the position of the robot in room, the plan of which is stored in memory.

Key words: computer vision, robotics, navigation.

«Национальный исследовательский университет» МЭИ»

в г. Смоленске

Поступила в редакцию 11.12.2013.