Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 12. -

Вып. 4. - 2013. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-40-html/TITL-40.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-40-html/cont.htm

УДК 621.391.161

КОРРЕЛЯЦИОННАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ В СИСТЕМАХ ТЕХНИЧЕСКОГО ЗРЕНИЯ

Ó 2013 г. Прокофьева П. А., Якименко Ю. И.

(prokofjeva.doc)

В статье изложен способ обработки изображений в системах технического зрения, необходимый для оценки динамики технологического процесса. Предлагаемый способ основан на использовании изменения величины коэффициента корреляции для оценки степени развития технологического объекта. На основе этого способа реализован алгоритм обработки изображений систем технического зрения и доказана его работоспособность

Ключевые слова: система технического зрения, технологический процесс, коэффициента корреляции, алгоритм обработки изображений.

В основу способа обработки изображений систем технического зрения, предназначенного для оценки динамики технологического процесса, предлагается включить расчет нормированного коэффициента корреляции между двумя матрицами изображений, зафиксированными через равные установленные интервалы времени.

где v_i,j– элементы массива первичного изображения, полученного в момент времени t₁=0;

w_i,j– элементы массива вторичного изображения, полученного в момент времени t₂=0+∆t.

Нормированный коэффициент корреляции принимает значение от 0 до 1. В случае, когда изменений в изображении не наблюдается, величина коэффициента стремится к 1. Если изменения в изображении происходят, то величина коэффициента корреляции будет стремиться к 0.

Считается, если коэффициент корреляции стал ниже 0,5, то изменения можно считать значительными. Поэтому, учитывая скорость, особенности протекания технологического процесс и степень допустимых изменений, необходимо экспериментально установить величину порога принятия решения и временные сдвиги между наблюдаемыми изображениями.

В основе корреляционного способа лежит процедура сравнения коэффициента корреляции с пороговым значением. Величина коэффициента корреляции ниже порогового значения свидетельствует о динамике (изменениях),происходящей в технологическом процессе, в противном случае динамика (изменения) отсутствует (рисунок 1).

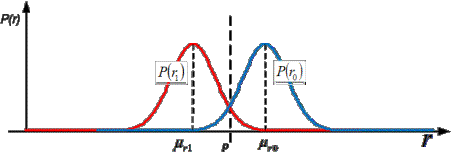
Рисунок 1 – Законы распределения вероятностей распределения значений коэффициентов корреляции

Таким образом, пороговая обработка полученных значений коэффициентов корреляции позволит сделать вывод о динамике (изменениях) технологического процесса и перейти к формированию команд управления.

Корреляционный алгоритм обработки изображений содержит ряд действий, которые можно условно разделить на подготовительную часть и основную часть, непосредственно расчет и пороговая обработка результата, итогом которой становится вывод - есть изменения в развитии объекта на время наблюдения или нет. Исходя из этого вывода, вырабатываются управляющий сигнал на исполнительный механизм системы дозированной подачи активной жидкости к выбранному объекту (рисунок 2).

Подготовительная часть содержит два этапа последовательного получение массивов изображения развивающегося объекта через установленный период времени T.

Основная часть содержит расчет нормированного коэффициента корреляции между двумя матрицами изображений, зафиксированными через равные установленные интервалы времени.

В ходе выполнения алгоритма нормированный коэффициент корреляции принимает значение от 0 до 1. В случае, когда изменений в изображении объекта не наблюдается, величина коэффициента стремится к 1. Если изменения в изображении объекта происходят, то величина коэффициента корреляции будет стремиться к 0.

Учитывая скорость, особенности протекания технологического процесс и степень допустимых изменений, экспериментально устанавливается величина порога принятия решения. Величина порога используется для выполнения блока сравнения с порогом, что приведет к принятию бинарного решения, есть изменения или их нет в процессе развития объекта наблюдения.

Исходя из результата принятого решения блоком формирования кода управления, будет сформирован управляющий сигнал, поступающий в систему дозированной подачи активной жидкости, обеспечивающей развитие объекта наблюдения.

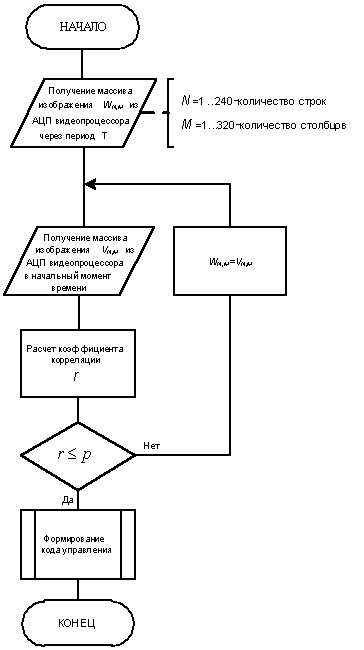
Рисунок 2 – Блок-схема корреляционного алгоритма обработки изображений

Для проведения предварительной оценки работоспособности и определения уровня порога принятия решения было проведено предварительное математическое моделирование с использованием математического пакета MathCad.

В качестве экспериментального видеопотока был использованы кадры видеофильма ускоренного развития грибоподобной структуры. Использовался фрагмент ускоренного видеофильма длительностью 4 минуты, в котором была сосредоточено 4 часа реального времени съемки.

Таким образом, протекание процесса грибоподобных структур было ускорено в 60 раз. Следовательно, при сдвижке между кадрами в 1 секунду реальный интервал будет соответствовать 1 минуте.

Образное представление пачек видеокадров полученных через равные промежутки времени, представлено на рисунке 3.

Рисунок 3 – Образное представление пачек видеокадров полученных через равные промежутки времени

Из видеопотока было вырезано 400 видеокадров, которые были сформированы через 1 с и разделены на четыре группы по 100 штук. Временной интервал между группами составляет 60 мин.

Для оценки величин коэффициентов корреляции между массивами изображений были рассчитаны нормированные коэффициенты корреляции. Оценка велась с целью установления интервала времени, после которого функционал начинает устойчиво работать.

Для этого была создана программа MathCad расчета корреляционных матриц на основе подготовленных выше пачек изображений(рисунок 4).

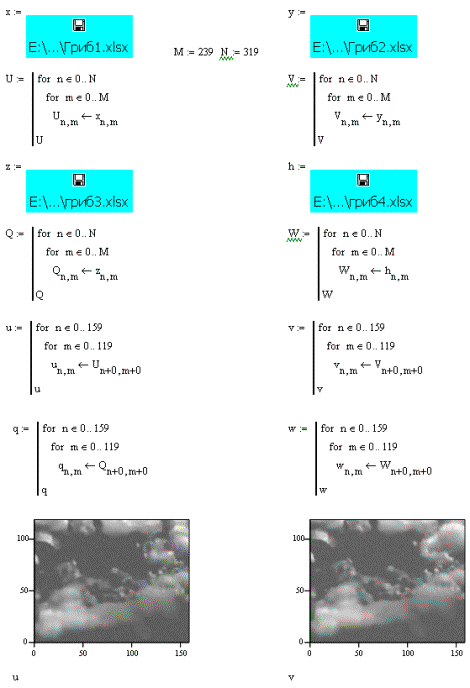
Рисунок 4 – Программа MathCad для расчета корреляционных матриц

Корреляционная матрица имеет вид, представленный на рисунке5. Информационной является первая строка, которая информирует о величине нормированного коэффициента корреляции. Элемент r₁₁=1 получен при расчете массива №1 первой пачки сам с собой. Элемент r₁₂=1 получен при расчете массива №1 первой пачки с массивом №1 второй пачки. Элемент r₁₃=1 получен при расчете массива №1 первой пачки с массивом №1 третий пачки. Элемент r₁₄=1 получен при расчете массива №1 первой пачки с массивом №1 четвертой пачки. Расчет повторялся для массивов с №2 – 100 для всех 4 пачек. Таким образом, получалась группа зависимостей коэффициента корреляции от временного сдвига. Примерный вид зависимостей коэффициента корреляции представлен на рисунке 6.

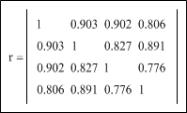
Рисунок 5 – Внешний вид рассчитанной корреляционной матрицы с выделенной информационной строкой

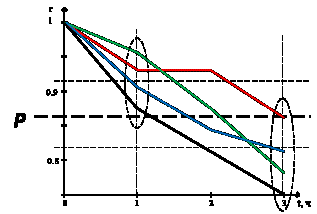
Рисунок 6. – Зависимости значений коэффициентов корреляции

от интерваловвремени наблюдения

Оценка значений коэффициентов корреляции между изображениями динамичного технологического процесса позволила зафиксировать изменения величин коэффициентов от интервалов времени наблюдения. Оптимальный временной интервал сдвига был выбран в количестве 120 мин.

Для дальнейших исследований необходимо исследовать чувствительность функционала – нормированный коэффициент корреляции от размера исследуемых изображений (электронного увеличения).Для исследования чувствительности от размера исследуемых изображений (электронного увеличения) несколько изображений были сегментированы в близи элементов, несущих информацию о развивающимся объекте (рисунок 7). Для них были рассчитаны зависимости величины коэффициента корреляции в зависимости от временного сдвига (рисунок 8)и от кратности электронного увеличения (рисунок 9).

а)	б)
в)	г)

Рисунок7. – Изменение вида изображений при уменьшении размерности (при электронном увеличении):

а) размер 240×320 – нет увеличени;

б) размер 120×180 – увеличение в 2 раза;

в) размер 60×90 – увеличение в 4 раза;

г) размер 30×45 – увеличение в 16 раза

Уменьшение размерности матрицы изображения приводит к повышению чувствительности, но при этом теряется информативность изображения. Следовательно, необходимо сохранять изображение объекта наблюдения в пределах кадра разделять его на сегменты и проводить расчет функционала для каждой части отдельно.Оптимальный размер сегмента для анализа изображения размером 240×320 был выбран 120×180 элементов, что предполагает деление изображения на 4 равные части.

а)

б)

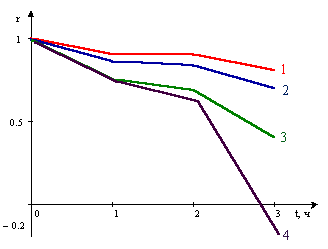
Рисунок 8. – а) зависимости величины коэффициента корреляции

рассчитанные для разных размеров в зависимости от временного сдвига:

1) Размер 240×320 – нет увеличения;

2) Размер 120×180 – увеличение в 2 раза;

3) Размер 60×90 – увеличение в 4 раза;

4) Размер 30×45 – увеличение в 16 раза.

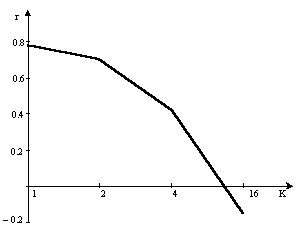
б) зависимости величины коэффициента корреляции, рассчитанные для разных размеров (К – кратность электронного увеличения) при сдвиге120 мин

При разделении кадра на сегменты (рисунок 9) анализ величин коэффициентов корреляции между сегментами, полученными в одном направления, не изменяются более чем на 10%.

Рисунок 9. – Сегментация массивов изображений одной пачки

Уменьшение размерности матрицы изображения приводит к повышению чувствительности функционала, но при этом терялась информативность изображения (рисунок 10).Необходимо сохранять изображение объекта наблюдения в пределах кадра, разделять его на сегменты и проводить расчет функционала для каждой части отдельно.

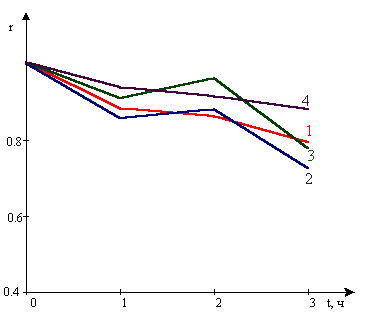
Рисунок 10. – Зависимости величины коэффициента корреляции рассчитанные для разных сегментов в зависимости от временного интервала

Оптимальный размер сегмента для анализа массива изображения размером 240×320 был выбран 120×180 элементов, что предполагает деление изображения на 4 равные части.

Для получения пороговых значений принятия решения о коррелированности между отдельными выборками используются в основном такие статистические критерии, как критерий идеального наблюдателя, критерий Неймана-Пирсона, критерий Байеса, критерий максимального правдоподобия. Эти критерий относятся к группе параметрических критериев, которые включают в формулу расчета параметры распределения, то есть средние и дисперсии [1]. Причем, эти критерии применялись без проверки распределения «на нормальность», что заведомо ошибочно, так как полученные в ходе математического моделирования значения коэффициента корреляции распределяются по неизвестному закону. Следовательно, применение параметрических методов оценки является затруднительным (таблица 1).

Из таблицы 1 видно, что параметрические критерии могут оказаться несколько более мощными, чем непараметрические, но только в том случае, если признак измерен по интервальной шкале и нормально распределен. С интервальной шкалой есть определенные проблемы. Лишь с некоторым приближением можно считать данные, представленные не в стандартизованных оценках, как интервальные. Кроме того, проверка распределения «на нормальность» требует достаточно сложных расчетов, результат которых заранее неизвестен.

Может оказаться, что распределение признака отличается от нормального, и так или иначе все равно придется обратиться к непараметрическим критериям.

Непараметрические критерии лишены всех этих ограничений и не требуют таких длительных и сложных расчетов. По сравнению с параметрическими критериями они ограничены лишь в одном – с их помощью невозможно оценить взаимодействие двух или более условий или факторов, влияющих на изменение признака. Эту задачу может решить только дисперсионный двухфакторный анализ.

Таблица 1 – Возможности и ограничения критериев принятия решения

Параметрические	Непараметрические
1. Позволяют прямо оценить различия в средних, полученных в двух выборках (t -критерий Стьюдента).	Позволяют оценить лишь средние тенденции, например, ответить на вопрос, чаще ли в выборке А встречаются более высокие, а в выборке Б - более низкие значения признака (критерии Q, U, φ* и др.).
2. Позволяют прямо оценить различия в дисперсиях (критерий Фишера).	Позволяют оценить лишь различия в диапазонах вариативности признака (критерий φ*).
3. Позволяют выявить тенденции изменения признака при переходе от условия к условию (дисперсионный однофакторный анализ), но лишь при условии нормального распределения признака.	Позволяют выявить тенденции изменения признака при переходе от условия к условию при любом распределении признака (критерии тенденций L и S).
4. Позволяют оценить взаимодействие двух и более факторов в их влиянии на изменения признака (двухфакторный дисперсионный анализ).	Эта возможность отсутствует.
5. Экспериментальные данные должны отвечать двум, а иногда трем, условиям: а) значения признака измерены по интервальной шкале; б) распределение признака является нормальным; в) в дисперсионном анализе должно соблюдаться требование равенства дисперсий в ячейках комплекса.	Экспериментальные данные могут не отвечать ни одному из этих условий: а) значения признака могут быть представлены в любой шкале, начиная от шкалы наименований; б) распределение признака может быть любым и совпадение его с каким-либо теоретическим законом распределения необязательно и не нуждается в проверке; в) требование равенства дисперсий отсутствует.
6. Математические расчеты довольно сложны.	Математические расчеты по большей части просты и занимают мало времени (за исключением критериев χ^2 и λ).
7. Если условия, перечисленные в п.5, выполняются, параметрические критерии оказываются несколько более мощными, чем непараметрические.	Если условия, перечисленные в п.5, не выполняются, непараметрические критерии оказываются более мощными, чем параметрические, так как они менее чувствительны к «засорениям».

Для достоверности была произведена проверка на «нормальность» полученных в ходе моделирования данных, с помощью критерия χ². По полученным данным было сделано предположение, что распределения признака распознавания ɛ отличаются от нормального распределения. В связи с этим, для решения задачи определения пороговых значений принятия решений применим непараметрический метод оценки.

Непараметрические методы математической статистики – методы непосредственной оценки и проверки гипотез о теоретическом распределении вероятностей и тех или иных его общих свойствах (симметрии, независимости и т. п.) по результатам наблюдений. Название «Непараметрические методы» подчёркивает их отличие от классических (параметрических) методов, в которых предполагается, что неизвестное теоретическое распределение принадлежит какому-либо семейству, зависящему от конечного числа параметров (например, семейству нормальных распределений), и которые позволяют по результатам наблюдений оценивать неизвестные значения этих параметров и проверять те или иные гипотезы относительно их значений. Особенность непараметрических методов в отличие от классических методов состоит в независимости от неизвестного теоретического распределения.

Одним из непараметрических методов математической статистики является критерий проверки эмпирических распределений – критерий Колмогорова-Смирнова [2].

Для расчета порогового значениякритерия Колмогорова-Смирнова необходимо:

1.Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты, полученные в распределении 1 (первый столбец) и 2 (второй столбец).

2. Подсчитать эмпирические частоты по каждому разряду для распределения 1 и 2 по формуле:

,

где – эмпирическая частота в данном разряде,

– количество наблюдений в 1(2) выборке.

Занести эмпирические частоты распределения 1 и 2 в третий и четвертый столбец таблицы соответственно.

3. Подсчитать накопленные эмпирические частоты для распределения 1 и 2 по формуле:

,

где – частота, накопленная на предыдущих разрядах;

– порядковый номер разряда;

– частота данного разряда.

Полученные результаты записать в пятый и шестой столбцы соответственно.

4. Подсчитать разности между накопленными частотами по каждому разряду.

Записать в седьмой столбец абсолютные величины разностей, без их знака. Обозначить их как d.

5. Определить по седьмому столбцу наибольшую абсолютную величину разности.

6. Подсчитать значение критерия λ по формуле:

,

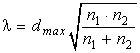где – количество наблюдений в первой (второй) выборке.

7. По табличным данным определить, какому уровню статистической значимости соответствует полученное значение λ.

Если λ_эмп>1,36, различия между распределениями достоверны, а соответствующее λ число наблюдений является пороговым значением.

Ограничения критерия Колмогорова-Смирнова

1. Критерий требует, чтобы выборка была достаточно большой. При сопоставлении двух эмпирических распределений необходимо чтобы n_1,2≥50. Сопоставление эмпирического распределения с теоретическим иногда допускается при n>5.

2. Разряды должны быть упорядочены по нарастанию или убыванию какого-либо признака. Они обязательно должны отражать какое-то однонаправленное его изменение.

В результате предварительного имитационного моделирования были получены две случайные выборки значений коэффициентов корреляции одна (N) при малых временных сдвигах (до 1 часа), а другая (M) ─ при временном сдвиге (более 2 часов).

Выборки были проверены на нормальное распределение при помощи специализированной программы. Результат проверки оказался отрицательным (рисунки 11, 12).

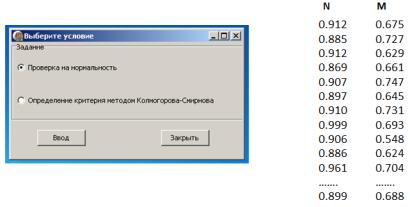
Рисунок 11 – Внешний вид интерфейса программы для оценки нормальности представленных выборок

Поскольку выборки не имеют нормального распределения, было решено отказаться от традиционных статистических критериев (Неймана-Пирсона, «Идеального наблюдателя», Байесовского и т.д.) и оценивать величины порога принятия решения с использованием критерия Колмогорова-Смирнова.

Поскольку выборки не имеют нормального распределения, было решено оценивать величины порога принятия решения с использованием критерия Колмогорова-Смирнов. Величина оценки порога составила 0,8.

Рисунок 12 – Внешний вид интерфейса программы для оценки порога

Принятия решения в соответствии с критерием Колмогорова-Смирнова

Доказательство работоспособности предложенного корреляционного алгоритма было проведено в среде Matlab&SimulinkR2012b/R2013a. Для этого была создана программа, листинг которой представлен ниже:

f1=imread('C:\Users\YuROck\Documents\MATLAB\гриб1.bmp')

g1=rgb2gray(f1) %преобразование картины в серый цвет работа с одной матрицей

H1=im2uint16(g1)%изменение глубины цвета

%то же самое со вторым рисунком

f2=imread('C:\Users\YuROck\Documents\MATLAB\гриб2.bmp')

g2=rgb2gray(f2) %преобразование картины в серый цвет работа с одной матрицей

H2=im2uint16(g2)%изменение глубины цвета

c=corr2(H1,H2)

porog=0.8

if c>=porog

disp('Нет изменений')

else

disp('Есть изменения')

При подаче двух пачек массивов изображений в количестве по 100 штук в каждом сдвинутые относительно друг друга на 120 минут, вероятность определения изменений в объекте составило 0,89. Что свидетельствует о работоспособности предложенного способа обработки изображений систем технического зрения, предназначенного для оценки динамики технологического процесса.

Таким образом, проведенные исследования привели к следующим результатам:

1. Оценка значений коэффициентов корреляции между изображениями динамичного технологического процесса позволила зафиксировать изменения величин коэффициентов от интервалов времени наблюдения. Оптимальный временной интервал сдвига был выбран в количестве 120 мин.

2. Уменьшение размерности матрицы изображения приводит к повышению чувствительности функционала, но при этом терялась информативность изображения.

3. Необходимо сохранять изображение объекта наблюдения в пределах кадра, разделять его на сегменты и проводить расчет функционала для каждой части отдельно. Оптимальный размер сегмента для анализа изображения размером 240×320 был выбран 120×180 элементов, что предполагает деление изображения на 4 равные части.

4. Поскольку выборки не имеют нормального распределения, было решено оценивать величины порога принятия решения с использованием критерия Колмогорова-Смирнов. Величина оценки порога составила 0,8.

5. Оценка работоспособности способа и алгоритма обработки изображений систем технического зрения, предназначенного для оценки динамики технологического процесса, подтвердило его работоспособность. Так, при подаче двух пачек массивов изображений в количестве по 100 штук в каждом сдвинутые относительно друг друга на 120 минут, вероятность определения изменений в объекте составило 0,89.

Литература

1. Гансалес Р., Вудс Р. Цифровая обработка изображений. М., Техносфера, 2005.1012 с.

2. Сидоренко Е. Методы математической обработки в психологии. М., Речь, 2005.205 с.

CORRELATION PROCESSING OF IMAGES IN SYSTEMS OF TECHNICAL SIGHT

Prokofieva P. A. YakimenkoYu. I.

In article the way of processing of images in systems of the technical sight, necessary for an assessment of dynamics of technological process is stated. The offered way is based on use of change of size of coefficient of correlation for an assessment of extent of development of technological object. On the basis of this way the algorithm of processing of images of systems of technical sight is realized and its working capacity is proved.

Key words: System of technical sight, technological process, correlation coefficient, algorithm of processing of images.

Филиал ФГБОУ ВПО «Национальный исследовательский университет»

МЭИ» в г. Смоленске

Поступила в редакцию 12.12.2013.