Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 13. -

Вып. 1. - 2014. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-41-html/TITL-41.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-41-html/cont.htm

 

УДК 004.932.2

 

ОПТИМИЗИРОВАННОЕ ПРЕОБРАЗОВАНИЕ ХАФА ДЛЯ ОБРАБОТКИ ПОКАЗАНИЙ ДАЛЬНОМЕРОВ

 

Ó 2014 г. Киселев К. О.

 

(kiselev.doc)

 

В работе изложен алгоритм вычисления классического преобразования Хафа для случая, когда входными данными являются показания дальномеров. Так как преобразование Хафа вычисляется для изображения, а показания дальномеров обычно представлены в виде векторов в полярной системе координат, возникает необходимость адаптации классического преобразование Хафа к особенностям входных данных.

Ключевые слова: преобразование Хафа, цифровая обработка изображений, обработка показаний дальномеров, поиск прямых.

 

         Преобразование Хафа[1] в обработке изображений применяется для определения расположения объектов на монохромном изображении. Классическое преобразование Хафа применяется для поиска прямых на изображении. Поиск прямых в данных от дальномеров актуален тем, что большинство зданий и помещений имеют прямоугольную форму и в показаниях дальномеров (для случая двумерного пространства) выглядят прямыми линиями.

         Для применения классического преобразования Хафа набор входных данных (φi, ri) необходимо сначала преобразовать в двумерное изображение достаточного размера, чтобы вместить все точки (φi, ri), при этом точка расположения дальномера – начало системы координат, в которой представлены входные данные смещается к центру изображения, а преобразование Хафа принимает за начальную точку нижний левый угол изображения, что неудобно для дальнейшей обработки данных.

         Выходными данными преобразования Хафа является двумерный массив H(p, θ), называемый накопительным пространством. Координаты локального максимума в этом пространстве определяют найденные прямые линии в виде:

         где p и θ – определенные с помощью преобразования Хафа параметры прямой.

         При заполнении накопительного пространства для каждой не нулевой точки Ax,y входного изображения вычисляются все возможные проходящие через нее прямые. Через каждую точку Ax,y может проходить бесконечное число прямых, удовлетворяющих уравнению

         Изменяя θi от -90 до 90 градусов с шагом Δθ и округляя вычисленные по (2) значения px,y(θi) до ближайшего p'i=n*Δp, где n – целое, а Δp – шаг расчета по расстоянию, получаем массив (pi',θi), содержащий набор параметров прямых, проходящих через точку Ax,y.

         Далее значение каждой точки H(pi',θi) инкрементируется. Таким образом осуществляется голосование точками входного изображения A за проходящие через них прямые.

         Найдя локальные максимумы в H(p,θ), определим все найденные прямые. Каждому локальному максимуму под номером j с координатами (pj,θj) соответствует прямая на изображении, определяемая выражением (1), где p=pj, θ=θj. Координаты при этом отсчитываются от левого нижнего угла изображения.

         Так осуществляется вычисление преобразования Хафа для изображения.

         При обработке показаний дальномеров на входе мы имеем список точек (φi,ri) длинной N. Для обработки таких данных потребуется предварительно преобразовать их в двумерное изображение размером rmax x rmax. Такой алгоритм имеет вычислительную сложность

O=(rmax/Δr)2*180/Δθ       (3)

         Стоит отметить, что сложность напрямую не зависит от объема входных данных N, но зависит от самих данных – максимального значения расстояния rmax.

         Чтобы избежать лишних вычислений необходимо изменить формулу (2) с учетом того, что входными данными является набор точек Di=(φi,ri):

         Аналогично (2) изменяя θi от -90 до 90 градусов с шагом Δθ и округляя вычисленные по (4) значения pi(θi) до ближайшего pi'=n*Δp, где n – целое, а Δp – шаг расчета по расстоянию, получаем массив (pi',θi), содержащий набор прямых, проходящих через i точку входных данных. Для каждой i точки из D инкрементируя точки накопительного пространства H(p'i,θi) в результате получим двумерный массив преобразования Хафа, аналогичный массиву, полученному с использованием классического алгоритма. При этом модифицированный алгоритм имеет сложность

O=N*180/Δθ        (5)

         Так же при этом не требуется дополнительного расхода оперативной памяти для хранения построенного по точкам Di изображения Ax,y.

         Рассмотрим примеры работы обоих алгоритмов на примере линии с параметрами θ=45o, p=10. С помощью Matlab  вычислим расстояния ri до такой линии из точки с координатами (0,0) в направлениях угла φi. Получим набор точек Di:

 

Рисунок 1 – массив Di в Matlab

 

         Далее по классическому алгоритму его необходимо преобразовать в изображение A размером 33x33

 

 

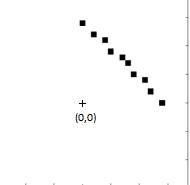
Рисунок 2  – Входное изображение A

 

         Вычислим классическое и оптимизированное преобразования Хафа.

 

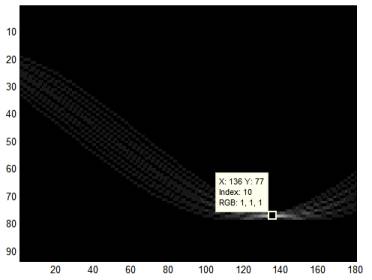
Рисунок 3 – Результат вычисления преобразования Хафа классическим методом

 

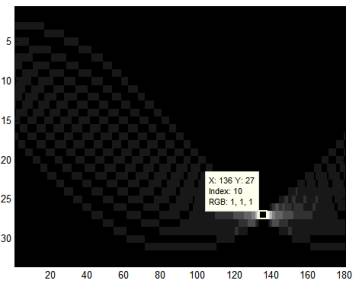
Рисунок 4 – Результат вычисления преобразования Хафа оптимизированным методом

 

         Из изображений 3 и 4 видим, что координата X, соответствующая параметру θ, совпадает в обоих случаях, т.к. масштабы этих осей совпадают. Координаты Y отличаются, т.к. накопительные пространства имеют разный размер и преобразования принимают за начало координат разные точки. У оптимизированного преобразования Хафа оно имеет размер 180x33, а у стандартного 180x93. Это происходит из-за того, что классическое преобразование Хафа ведет отсчет координат из левого нижнего края исходного изображения, которое должно иметь размер 2rmax2rmax чтобы полностью вместить полученные данные с дальномеров. Т.е. p может изменяться в пределах . При вычислении оптимизированного преобразования Хафа p изменяется в пределах .

         Для правильной интерпретации параметров прямых результатом работы преобразований Хафа является не только накопительное пространство H, но и еще 2 массива для преобразования координат локального максимума в параметры прямой. А для классического преобразования Хафа потребуется дополнительный пересчет параметров найденной прямой в новую систему координат, связанную с центром изображения. Разработанное оптимизированное преобразование Хафа избавлено от этого недостатка.

         Разработанный алгоритм вычисления преобразования Хафа удобен для использования при вычислении перемещений робота, оснащенного дальномером, в помещениях, т.к. они почти всегда имеют прямоугольную форму. Аналогичным методом возможно и вычисление трехмерного преобразования Хафа для поиска плоскостей во входном облаке точек (ri, φi, θi).

 

Литература

 

1.     Robyn Owens, "Computer Vision IT412, Lecture 6" http://www.dai.ed.ac.uk/CVonline/LOCAL_COPIES/OWENS/LECT6/node3.html, 1997

2.     Гансалес Р., Вудс Р. Цифровая обработка изображений. М., Техносфера, 2005.1012 с.

3.     Гонсалес Р., Вудс Р., Эддинс С. Цифровая обработка изображений в среде MATLAB. Москва: Техносфера, 2006. 616с.

 

 

OPTIMIZED HOUGH TRANSFORM FOR RANGEFINDERS DATA

 

Kiselev K. O.

 

The paper presents an algorithm for computing the classical Hough transform for the case where the input data are indications rangefinders . Since the Hough transform is calculated for the image and the reading range finders are usually represented as vectors in a polar coordinate system , there is a need to adapt the classical Hough transform to the characteristics of the input data.

Key words: Hough transform , digital image processing , treatment indications rangefinders, lines search .

 

 

Филиал ФГБОУВПО

«Национальный исследовательский университет»МЭИ»

в г. Смоленске

Поступила в редакцию 23.02.2014.